备考2024届高考数学一轮复习讲义第六章平面向量复数第4讲余弦定理正弦定理

这是一份备考2024届高考数学一轮复习讲义第六章平面向量复数第4讲余弦定理正弦定理，共8页。
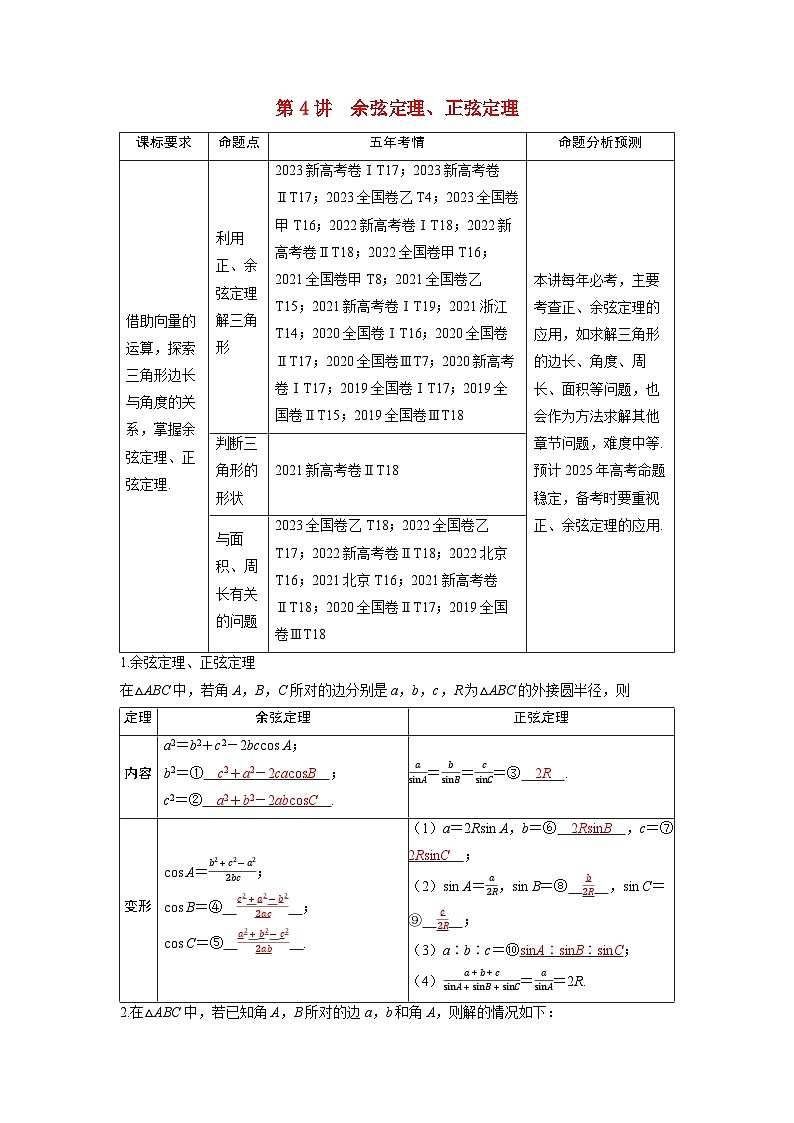
在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC的外接圆半径，则
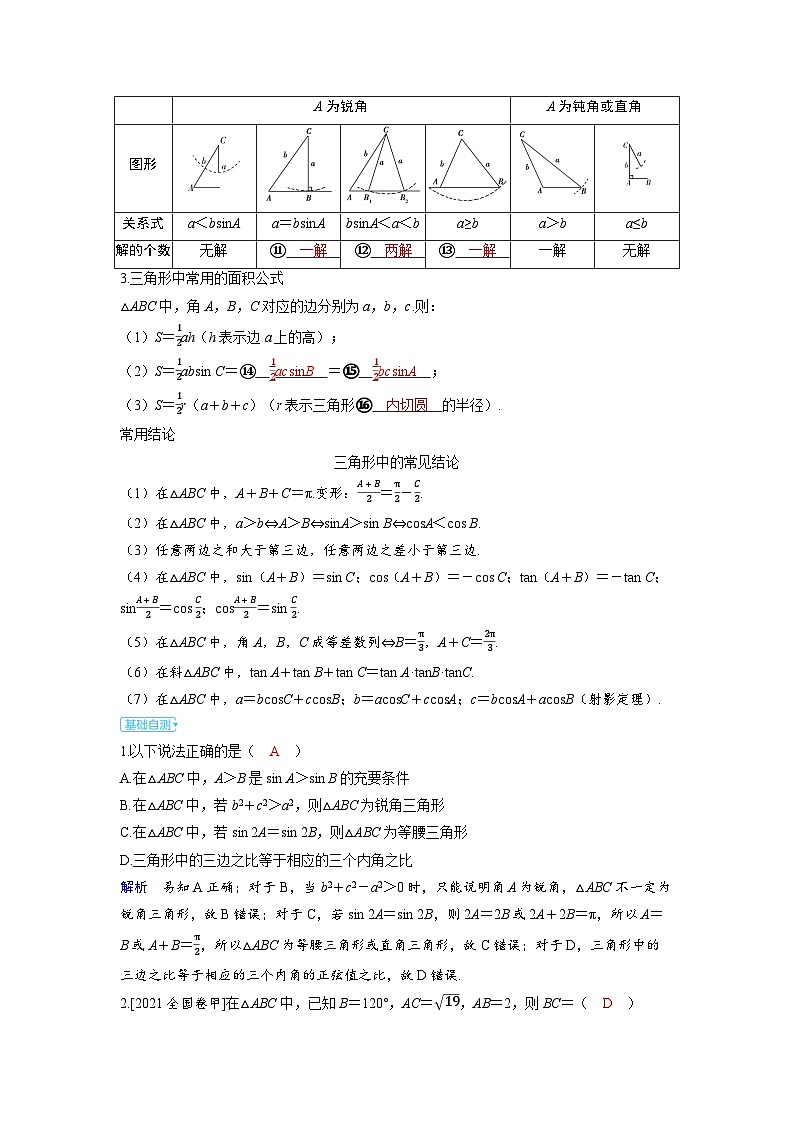
2.在△ABC中，若已知角A，B所对的边a，b和角A，则解的情况如下：
3.三角形中常用的面积公式
△ABC中，角A，B，C对应的边分别为a，b，c.则：
（1）S＝12ah（h表示边a上的高）；
（2）S＝12absin C＝⑭ 12acsinB ＝⑮ 12bcsinA ；
（3）S＝12r（a＋b＋c）（r表示三角形⑯ 内切圆 的半径）.
常用结论
三角形中的常见结论
（1）在△ABC中，A＋B＋C＝π.变形：A＋B2＝π2－C2.
（2）在△ABC中，a＞b⇔A＞B⇔sinA＞sin B⇔csA＜cs B.
（3）任意两边之和大于第三边，任意两边之差小于第三边.
（4）在△ABC中，sin（A＋B）＝sin C；cs（A＋B）＝－cs C；tan（A＋B）＝－tan C；sinA＋B2＝cs C2；csA＋B2＝sin C2.
（5）在△ABC中，角A，B，C成等差数列⇔B＝π3，A＋C＝2π3.
（6）在斜△ABC中，tan A＋tan B＋tan C＝tan A·tanB·tanC.
（7）在△ABC中，a＝bcsC＋ccsB；b＝acsC＋ccsA；c＝bcsA＋acsB（射影定理）.
1.以下说法正确的是（ A ）
A.在△ABC中，A＞B是sin A＞sin B的充要条件
B.在△ABC中，若b2＋c2＞a2，则△ABC为锐角三角形
C.在△ABC中，若sin 2A＝sin 2B，则△ABC为等腰三角形
D.三角形中的三边之比等于相应的三个内角之比
解析 易知A正确；对于B，当b2＋c2－a2＞0时，只能说明角A为锐角，△ABC不一定为锐角三角形，故B错误；对于C，若sin 2A＝sin 2B，则2A＝2B或2A＋2B＝π，所以A＝B或A＋B＝π2，所以△ABC为等腰三角形或直角三角形，故C错误；对于D，三角形中的三边之比等于相应的三个内角的正弦值之比，故D错误.
2.[2021全国卷甲]在△ABC中，已知B＝120°，AC＝19，AB＝2，则BC＝（ D ）
A.1B.2C.5D.3
解析 由余弦定理得AC2＝AB2＋BC2－2AB·BC·cs B，得BC2＋2BC－15＝0，解得BC＝3或BC＝－5（舍去）.故选D.
3.[多选]记△ABC的内角A，B，C的对边分别为a，b，c，则符合下列条件的△ABC有且只有一个的是（ AC ）
A.a＝2，b＝1，A＝45°B.a＝1，b＝2，c＝3
C.b＝c＝1，B＝45°D.a＝1，b＝2，A＝100°
解析 对于A，由正弦定理得1sinB＝2sin45°，所以sin B＝12，又a＞b，所以B＝30°，所以满足条件的三角形只有一个；
对于B，a＋b＝c，构不成三角形；
对于C，b＝c＝1，所以B＝C＝45°，A＝90°，所以满足条件的三角形只有一个；
对于D，a＜b，所以A＜B，而A＝100°，所以没有满足条件的三角形.
4.已知2a＋1，a，2a－1是钝角三角形的三边，则实数a的取值范围是 （2，8） .
解析 ∵2a＋1，a，2a－1是三角形的三边，∴2a+1>0，a>0，2a－1>0，解得a＞12.显然2a＋1是三角形的最大边，则要使2a＋1，a，2a－1构成三角形，需满足a＋2a－1＞2a＋1，解得a＞2.设最大边对应的角为θ（钝角），则cs θ＝a2＋（2a－1）2－（2a+1）22a（2a－1）＜0，
∴a2＋（2a－1）2－（2a＋1）2＜0，即a2－8a＜0，解得0＜a＜8.
又a＞2，∴a的取值范围是（2，8）.
5.在△ABC中，A＝60°，AC＝4，BC＝23，则△ABC的面积等于 23 .
解析 设△ABC中，角A，B，C对应的边分别为a，b，c.
由题意及余弦定理得cs A＝b2＋c2－a22bc＝16+c2－122×4×c＝12，解得c＝2，所以S△ABC＝12bcsin A＝12×4×2×sin 60°＝23.
研透高考 明确方向
命题点1 利用正、余弦定理解三角形
例1 （1）[2023全国卷乙]在△ABC中，内角A，B，C的对边分别是a，b，c，若acsB－bcsA＝c，且C＝π5，则B＝（ C ）
A.π10B.π5C.3π10D.2π5
解析 因为acsB－bcsA＝c，所以由正弦定理得sin A·csB－sin BcsA＝sin C＝sin（B＋A），则2sin BcsA＝0.在△ABC中，sin B≠0，则cs A＝0，A＝π2，所以B＝π－A－C＝π－π2－π5＝3π10，故选C.
（2）[2021全国卷乙]记△ABC的内角A，B，C的对边分别为a，b，c，面积为3，B＝60°，a2＋c2＝3ac，则b＝ 22 .
解析 由题意得S△ABC＝12acsin B＝34ac＝3，则ac＝4，所以a2＋c2＝3ac＝3×4＝12，所以b2＝a2＋c2－2accs B＝12－2×4×12＝8，则b＝22.
方法技巧
应用正、余弦定理的解题技巧
（1）求边：利用正弦定理变形公式a＝bsinAsinB等或余弦定理a2＝b2＋c2－2bccs A等求解.
（2）求角：利用正弦定理变形公式sin A＝asinBb等或余弦定理变形公式cs A＝b2＋c2－a22bc等求解.
（3）利用式子的特点转化：若出现a2＋b2－c2＝λab的形式，则用余弦定理；若等式两边是关于边或角的正弦的齐次式，则用正弦定理.
训练1 （1）[全国卷Ⅰ]△ABC的内角A，B，C的对边分别为a，b，c.已知asinA－bsinB＝4csin C，cs A＝－14，则bc＝（ A ）
A.6B.5C.4D.3
解析 由题意及正弦定理得b2－a2＝－4c2，所以由余弦定理得，cs A＝b2＋c2－a22bc＝－3c22bc＝－14，得bc＝6.故选A.
（2）[全国卷Ⅰ]△ABC的内角A，B，C的对边分别为a，b，c.已知sin B＋sin A·（sin C－cs C）＝0，a＝2，c＝2，则C＝（ B ）
A.π12B.π6C.π4D.π3
解析 因为sin B＋sin A（sin C－cs C）＝0，所以sin（A＋C）＋sin A·sinC－sin A·csC＝0，所以sin AcsC＋cs Asin C＋sin Asin C－sin AcsC＝0，整理得sin C（sin A＋cs A）＝0.因为sin C≠0，所以sin A＋cs A＝0，所以tan A＝－1.因为A∈（0，π），所以A＝3π4，由正弦定理得sin C＝c·sinAa＝2×222＝12，又0＜C＜π4，所以C＝π6.故选B.
命题点2 判断三角形的形状
例2 在△ABC中，a，b，c分别为角A，B，C的对边，c－a2c＝sin2B2，则△ABC的形状为（ A ）
A.直角三角形
B.等边三角形
C.等腰三角形或直角三角形
D.等腰直角三角形
解析 由cs B＝1－2sin2B2，得sin2B2＝1－csB2，所以c－a2c＝1－csB2，即cs B＝ac.
解法一 由余弦定理得cs B＝a2＋c2－b22ac＝ac，即a2＋c2－b2＝2a2，所以a2＋b2＝c2，所以△ABC为直角三角形，但无法判断两直角边是否相等.
解法二 由正弦定理得cs B＝sinAsinC，又sin A＝sin（B＋C）＝sin BcsC＋cs BsinC，所以cs BsinC＝sin BcsC＋cs BsinC，即sin BcsC＝0，又sin B≠0，所以cs C＝0，又角C为△ABC的内角，所以C＝π2，所以△ABC为直角三角形，但无法判断两直角边是否相等.
命题拓展
[变条件]将例2中的条件“c－a2c＝sin2B2”改为“sinAsinB＝ac，（b＋c＋a）（b＋c－a）＝3bc”，则△ABC的形状为 等边三角形 .
解析 因为sinAsinB＝ac，所以由正弦定理得ab＝ac，所以b＝c.又（b＋c＋a）（b＋c－a）＝3bc，所以b2＋c2－a2＝bc，所以由余弦定理得cs A＝b2＋c2－a22bc＝bc2bc＝12.因为A∈（0，π），所以A＝π3，所以△ABC是等边三角形.
方法技巧
判断三角形形状的方法
（1）化为边：通过正、余弦定理将角化边，利用因式分解、配方等得出边之间的关系进行判断.判断技巧：
（2）化为角：通过正、余弦定理将边化角，通过三角恒等变换公式、三角形的内角和定理得出角的大小或角之间的关系.
注意 （1）不能随意约掉公因式，要移项、提取公因式，否则会有遗漏一种形状的可能.（2）注意挖掘隐含条件，在变形过程中注意角的范围对三角函数值的影响.
训练2 [2021新高考卷Ⅱ]在△ABC中，角A，B，C所对的边分别为a，b，c，b＝a＋1，c＝a＋2.
（1）若2sin C＝3sin A，求△ABC的面积.
（2）是否存在正整数a，使得△ABC为钝角三角形？若存在，求a；若不存在，说明理由.
解析 （1）由2sin C＝3sin A及正弦定理，得2c＝3a.
又c＝a＋2，所以a＝4，c＝6，
所以b＝a＋1＝5.
由余弦定理，得cs A＝b2＋c2－a22bc＝25+36－162×5×6＝34.
又A∈（0，π），所以sin A＝74，
所以S△ABC＝12bcsin A＝12×5×6×74＝1574.
（2）存在.
由题意知c＞b＞a，要使△ABC为钝角三角形，需cs C＝a2＋b2－c22ab＝a2＋（a+1）2－（a+2）22×a×（a+1）＝a－32a＜0，
得0＜a＜3.
因为a为正整数，所以a＝1或a＝2.
当a＝1时，b＝2，c＝3，此时不能构成三角形；
当a＝2时，b＝3，c＝4，满足题意.
综上，存在正整数a＝2，使得△ABC为钝角三角形.
命题点3 与面积、周长有关的问题
角度1 面积问题
例3 [2023全国卷乙]在△ABC中，已知∠BAC＝120°，AB＝2，AC＝1.
（1）求sin∠ABC；
（2）若D为BC上一点，且∠BAD＝90°，求△ADC的面积.
解析 （1）由余弦定理得BC2＝AB2＋AC2－2AB·AC·cs∠BAC＝22＋12＋2×2×1×12＝7，得BC＝7.
由正弦定理得ACsin∠ABC＝BCsin∠BAC，则sin∠ABC＝1×327＝2114.
（2）解法一 如图，由sin∠ABC＝2114，得tan∠ABC＝35，
又tan∠ABC＝DAAB＝DA2，所以DA＝235，
故△ADC的面积为12DA·AC·sin（120°－90°）＝12×235×1×12＝310.
解法二 S△ABC＝12AC·AB·sin∠BAC＝12×1×2×32＝32，S△ADCS△BAD＝12AC·AD·sin∠CAD12AB·AD·sin∠BAD＝sin30°2×sin90°＝14，
故△ADC的面积为15S△ABC＝15×32＝310.
方法技巧
与面积有关问题的解题思路
1.利用面积公式S＝12absin C＝12acsin B＝12bcsin A求面积，一般是已知哪个角就使用哪一个公式.
2.与面积有关的问题，一般要用到正弦定理、余弦定理进行边和角的转化.
角度2 周长问题
例4 [2022全国卷乙]记△ABC的内角A，B，C的对边分别为a，b，c，已知sin Csin（A－B）＝sin Bsin（C－A）.
（1）证明：2a2＝b2＋c2；
（2）若a＝5，cs A＝2531，求△ABC的周长.
解析 （1）解法一 由sin Csin（A－B）＝sin Bsin（C－A）可得，sin CsinAcsB－
sin CcsAsin B＝sin B·sinCcsA－sin BcsCsinA，
结合正弦定理asinA＝bsinB＝csinC可得accsB－bccsA＝bccsA－abcsC，即accsB＋
abcsC＝2bccs A.
由余弦定理得a2＋c2－b22＋a2＋b2－c22＝b2＋c2－a2，整理得2a2＝b2＋c2.
解法二 因为A＋B＋C＝π，
所以sin Csin（A－B）＝sin（A＋B）sin（A－B）＝sin2Acs2B－cs2Asin2B＝sin2A（1－sin2B）－（1－sin2A）sin2B＝sin2A－sin2B.
同理有sin Bsin（C－A）＝sin（C＋A）sin（C－A）＝sin2C－sin2A，所以sin2A－sin2B＝sin2C－sin2A，
由正弦定理可得2a2＝b2＋c2.
（2）由（1）及a2＝b2＋c2－2bccs A得，a2＝2bccs A，所以2bc＝31.
因为b2＋c2＝2a2＝50，
所以（b＋c）2＝b2＋c2＋2bc＝81，得b＋c＝9，
所以△ABC的周长为a＋b＋c＝14.
方法技巧
与周长有关问题的解题思路
（1）若边长易求，直接求出边长，进而求出周长；
（2）若边长不易求，可利用整体思想，构造以两边长的和为未知数的方程求解，进而求出周长.
训练3 [2022北京高考]在△ABC中，sin 2C＝3sin C.
（1）求∠C；
（2）若b＝6，且△ABC的面积为63，求△ABC的周长.
解析 （1）因为sin 2C＝3sin C，
所以2sin C cs C＝3sin C.
因为C∈（0，π），所以sin C≠0，所以cs C＝32，C＝π6.
（2）因为△ABC的面积S＝12absin C＝12×a×6×12＝63，所以a＝43.
由余弦定理可得c2＝a2＋b2－2abcs C＝48＋36－72＝12，所以c＝23，所以△ABC的周长为a＋b＋c＝43＋6＋23＝6（3＋1）.课标要求
命题点
五年考情
命题分析预测
借助向量的运算，探索三角形边长与角度的关系，掌握余弦定理、正弦定理.
利用正、余弦定理解三角形
2023新高考卷ⅠT17；2023新高考卷ⅡT17；2023全国卷乙T4；2023全国卷甲T16；2022新高考卷ⅠT18；2022新高考卷ⅡT18；2022全国卷甲T16；2021全国卷甲T8；2021全国卷乙T15；2021新高考卷ⅠT19；2021浙江T14；2020全国卷ⅠT16；2020全国卷ⅡT17；2020全国卷ⅢT7；2020新高考卷ⅠT17；2019全国卷ⅠT17；2019全国卷ⅡT15；2019全国卷ⅢT18
本讲每年必考，主要考查正、余弦定理的应用，如求解三角形的边长、角度、周长、面积等问题，也会作为方法求解其他章节问题，难度中等.预计2025年高考命题稳定，备考时要重视正、余弦定理的应用.
判断三角形的形状
2021新高考卷ⅡT18
与面积、周长有关的问题
2023全国卷乙T18；2022全国卷乙T17；2022新高考卷ⅡT18；2022北京T16；2021北京T16；2021新高考卷ⅡT18；2020全国卷ⅡT17；2019全国卷ⅢT18
定理
余弦定理
正弦定理
内容
a2＝b2＋c2－2bccs A；
b2＝① c2＋a2－2cacsB ；
c2＝② a2＋b2－2abcsC .
asinA＝bsinB＝csinC＝③ 2R .
变形
cs A＝b2＋c2－a22bc；
cs B＝④ c2＋a2－b22ac ；
cs C＝⑤ a2＋b2－c22ab .
（1）a＝2Rsin A，b＝⑥ 2RsinB ，c＝⑦ 2RsinC ；
（2）sin A＝a2R，sin B＝⑧ b2R ，sin C＝⑨ c2R ；
（3）a∶b∶c＝⑩sinA∶sinB∶sinC；
（4）a＋b＋csinA＋sinB＋sinC＝asinA＝2R.
A为锐角
A为钝角或直角
图形
关系式
a＜bsinA
a＝bsinA
bsinA＜a＜b
a≥b
a＞b
a≤b
解的个数
无解
⑪ 一解
⑫ 两解
⑬ 一解
一解
无解
a2＋b2＜c2
cs C＜0
C为钝角
三角形为钝角三角形
a2＋b2＝c2
cs C＝0
C为直角
三角形为直角三角形
a2＋b2＞c2
cs C＞0
C为锐角
无法判断（只有C为最大角时才可得出三角形为锐角三角形）