资料中包含下列文件,点击文件名可预览资料内容





当前文件暂不支持在线预览,请下载使用
还剩19页未读,
继续阅读
成套系列资料,整套一键下载
北师大版数学八年级下册 1.1.2 《等腰三角形(2)》课件+分层练习(含答案解析)
展开
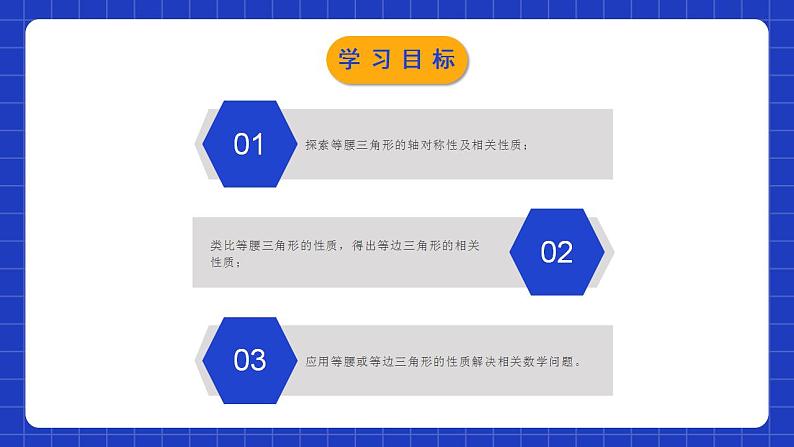
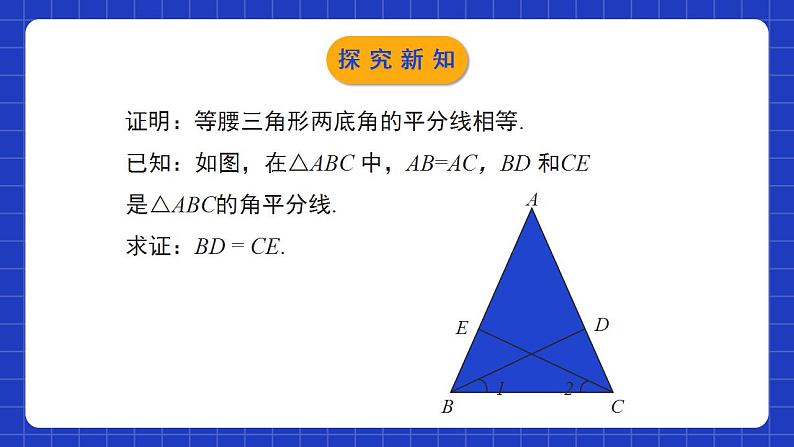
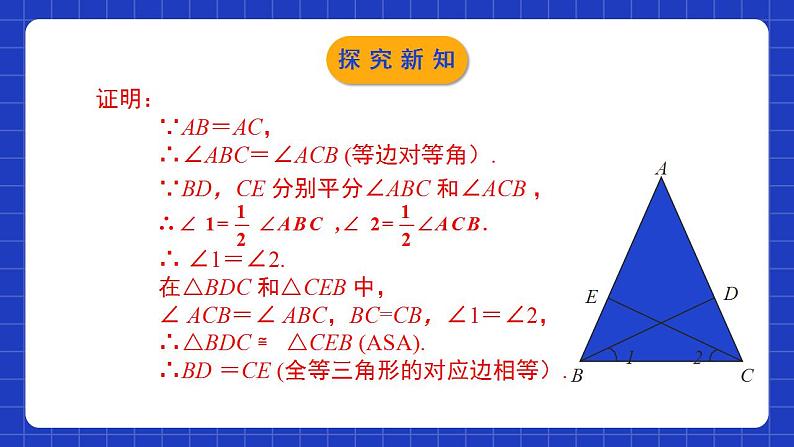
1.1.2等腰三角形(2)学习目标探索等腰三角形的轴对称性及相关性质;0102类比等腰三角形的性质,得出等边三角形的相关性质;应用等腰或等边三角形的性质解决相关数学问题。03知识点1 等腰三角形的两底角相等. 简称为等边对等角.知识点2 等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.通常称为:等腰三角形“三线合一”.情境导入 在七下我们已经知道了“三边相等的三角形是等边三角形”,生活中有很多等边三角形,如交通图标、台球室的三角架等,它们都是等边三角形.思考:在上一节课我们证明等腰三角形的两底角相等,那等边三角形的各角之间有什么关系呢?等腰三角形中有哪些相等的线段?情境导入等腰三角形的重要线段的性质 上节课我们证明了等腰三角形的“三线合一”,即顶角的平分线、底边上的高、底边上的中线. 试猜想等腰三角形的两底角的角平分线、两腰上的高、两腰上的中线有什么关系呢?探究新知画一画:在纸上画一个等腰三角形。它们在数量上有何关系?你能证明吗?在等腰三角形中作出两底角的平分线。探究新知 证明:等腰三角形两底角的平分线相等.已知:如图,在△ABC 中,AB=AC,BD 和CE 是△ABC的角平分线.求证:BD = CE.探究新知∵AB=AC,∴∠ABC=∠ACB (等边对等角).∵BD,CE 分别平分∠ABC 和∠ACB ,∴ ∠1=∠2.在△BDC 和△CEB 中,∠ ACB=∠ ABC,BC=CB,∠1=∠2,∴△BDC ≌ △CEB (ASA).∴BD =CE (全等三角形的对应边相等).证明:探究新知归纳总结 等腰三角形两腰上的中线相等吗?高呢?还有其他的结论吗?请你证明它们,并与同伴交流.等腰三角形两底角的平分线相等.探究新知已知:如图,在△ABC 中,AB=AC,BD和CE是△ABC的两腰上的中线. 求证:BD=CE.探究新知已知:如图,在△ABC 中,AB=AC,BD和CE是△ABC的两腰上的高. 求证:BD=CE.证明: ∵ AB=AC, ∴ ∠ABC= ∠ACB.∵ BD和CE是△ABC两腰上的高,∴ ∠BDC= 90°,∠BEC= 90° .在△BDC 和△CEB 中,∠ACB= ∠ABC, BC=CB, ∠BDC=∠BEC,∴ △BDC≌△CEB(AAS).∴ BD=CE(全等三角形的对应边相等).探究新知结论总结:等腰三角形两底角的平分线相等,两腰上的中线相等,两腰上的高相等.归纳总结探究新知归纳总结如果把等腰三角形两底角的平分线(二等分线)换成三等分线、四等分线,你能得到一个什么结论?把“等腰三角形两腰上的中线相等”改为“等腰三角形两腰上的三等分线(或四等分线)相等”是否也成立呢?过底边的端点且与底边夹角相等的两对应线段相等.两腰上距顶点等距的两点与底边顶点的连线段相等.探究新知等边三角形的性质 等边三角形是特殊的等腰三角形,那么等边三角形的内角有什么特征呢?定理 :等边三角形的三个内角都相等,并且每个角都等于60°.思考: 怎样证明这一定理?可以利用等腰三角形的性质进行证明.探究新知已知:如图, 在△ABC中,AB= AC=BC. 求证:∠A= ∠ B = ∠ C = 60°.证明:∵AB = AC,∴∠ B = ∠ C (等边对等角).又∵AC = BC,∴∠A= ∠ B (等边对等角).∴∠A= ∠ B = ∠ C.在△ABC中,∠A+∠ B+∠ C = 180°.∴∠A= ∠ B = ∠ C = 60°.探究新知(1)等边三角形是轴对称图形吗?如果是,它有几条对称轴?(2)等边三角形还有哪些特征?类比拓展:探究新知等边三角形的性质:1.等边三角形是轴对称图形。2.等边三角形的各角都相等,都等于60°3.等边三角形每个角的平分线和这个角的对边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴。归纳总结探究新知D随堂练习2.如图,在等边三角形ABC中,BD,CE是两条中线,则∠1的度数为( )A.90° B.30° C.120° D.150°C随堂练习3.若等腰三角形两腰上的高相交所成的钝角为100°,则顶角的度数为 ( )A.50° B.80 ° C.100 ° D.130 °B4.在△ABC中,AB=AC,BD、CE分别为∠ABC、∠ACB的平分线,BD=5,则CE= .5随堂练习5.如图,已知△ABC 是等边三角形,D,E,F 分别是三边AB,AC,BC 上的点,且DE⊥AC,EF⊥BC,DF⊥AB,计算△DEF 各个内角的度数.随堂练习因为△ABC 是等边三角形,所以∠A=∠B=∠C=60°.因为DE⊥AC,EF⊥BC,DF⊥AB,所以∠AED=∠EFC=∠FDB=90°.所以∠ADE=90°-∠A=90°-60°=30°.所以∠EDF=180°-30°-90°=60°.同理可得∠DEF=∠EFD=60°.即△DEF 各个内角的度数都是60°.解:随堂练习6.已知:如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,点M,N分别在AB,AC边上, AM=2MB, AN=2NC.求证:DM=DN.随堂练习随堂练习7. 如图,在△ABC中,D,E是BC的三等分点,且△ADE是等边三角形,求∠BAC的度数.解:∵ △ADE是等边三角形,∴ AD=DE=AE, ∠ADE= ∠DEA= ∠DAE =60°.∵ D,E是BC的三等分点,∴ BD=DE=EC,∴BD=AD,∴ ∠ABD= ∠BAD= 30°(三角形的外角性质).同理, ∠ ACE= ∠CAE= 30°.∴ ∠BAC= ∠BAD+ ∠DAE+ ∠BAD= 120°.随堂练习等边三角形的性质等边三角形的三个内角都相等,并且每个角都等于60°等腰三角形重要线段的性质底角的两条角平分线相等两条腰上的高相等两条腰上的中线相等课堂小结课程结束
相关资料
更多









