北师大版数学八年级下册 第一章《三角形的证明》单元小结 课件》课件+单元测试（含答案解析）

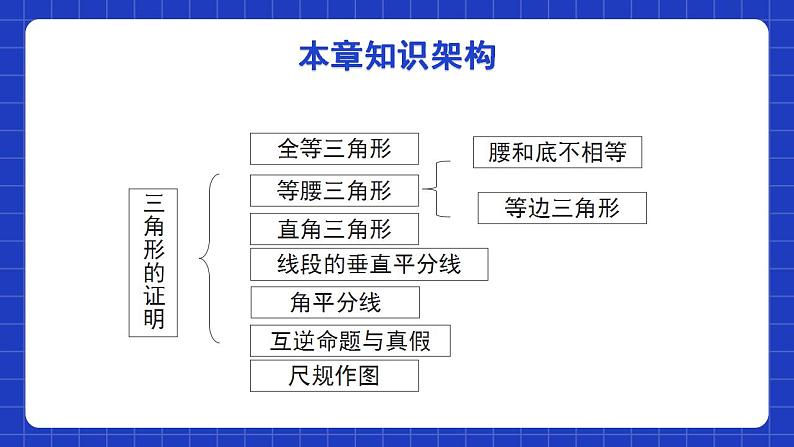
第一章数三角形的证明单元小结等腰三角形直角三角形线段的垂直平分线角平分线腰和底不相等等边三角形全等三角形互逆命题与真假尺规作图本章知识架构 本章所证明的命题大多与等腰三角形和直角三角形有关，主要包括哪些呢？1.等腰三角形（含等边三角形）、直角三角形的性质定理及判定定理；2.线段垂直平分线的性质定理及判定定理；3.角平分线的性质定理及判定定理.知识专题一.与等腰三角形、等边三角形有关的结论1.等腰三角形的性质（4）顶角的平分线、底边上的中线和底边上的高互相重合，简称“三线合一”.（3）两个底角相等，简称“等边对等角”；（2）是轴对称图形，等腰三角形的顶角平分线（或底边中线、底边高线）所在的直线是它的对称轴；（1）两腰相等；知识专题2. 等腰三角形的判定（1）有两边相等的三角形是等腰三角形；（2）如果一个三角形中有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）.说明：判定定理在同一个三角形中才能适用．知识专题3. 等边三角形的性质（1）等边三角形的三边都相等；（2）等边三角形的三个内角都相等，并且每一个角都等于60°；（3）是轴对称图形，对称轴是三条高（或三条中线、三条角平分线）所在的直线;（4）任意角平分线、角对边上的中线、对边上的高互相重合，简称“三线合一”.（5）在直角三角形中，30°的角所对的直角边等于斜边的一半.知识专题4. 等边三角形的判定（1）定义判定：三条边都相等的三角形是等边三角形.（2）判定定理1：三个角都相等的三角形是等边三角形.（3）判定定理2：有一个角是60°的等腰三角形是等边三角形.知识专题说明： 在证明一个三角形是等边三角形时，若已知或能求得三边相等则用定义来判定； 若已知或能求得三个角相等则用判定定理1来证明； 若已知等腰三角形且有一个角为60°，则用判定定理2来证明.知识专题二.与直角三角形有关的结论1.直角三角形的性质定理 性质1：直角三角形两直角边的平方和等于斜边的平方（勾股定理）．性质2：直角三角形的两个锐角互余．性质3：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半；知识专题2.直角三角形的判定定理（2）有两个角互余的三角形是直角三角形.（3）如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形．（1）有一个角是90°的三角形叫做直角三角形；知识专题三.线段的垂直平分线1. 线段垂直平分线的性质定理： 线段垂直平分线上的点到线段两端点的距离相等.2. 逆定理： 到线段两端点的距离相等的点在线段的垂直平分线上.知识专题3. 常见的基本作图： (1)过已知点作已知直线的垂线； (2)作已知线段的垂直平分线．4. 三角形的三边的垂直平分线的性质： 三角形的三边的垂直平分线相交于一点，且到三个顶点的距离相等.知识专题四.角平分线的性质与判定1. 性质定理：角平分线上的点到角两边的距离相等.2. 判定定理：在一个角的内部，到角两边距离相等的点在角的平分线上.3. 三角形的三条内角平分线的性质：三角形的三条内角平分线相交于一点，且到三边的距离相等.知识专题1．逆命题每一个命题都有逆命题，只要将原命题的条件改成结论，并将结论改成条件，便可以得到原命题的逆命题．五.命题和定理2．互逆命题在两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论是第二个命题的条件，那么这两个命题叫做互逆命题．知识专题3．逆定理如果一个定理的逆命题经过证明是真命题，那么，它也是一 个定理，这两个定理叫做互逆定理，其中一个叫做另一个的逆定理．注意：每个命题都有逆命题，但一个定理不一定有逆定理．知识专题考点1 等腰三角形的性质例1.如图，在△ABC中，AB＝AC，AD是中线，DE⊥AB，DF⊥AC，垂足分别为E，F，则下列四个结论中：①AB上任一点与AC上任一点到D的距离相等；②AD上任一点到AB，AC的距离相等；③∠BDE＝∠CDF；④∠1＝∠2.正确的有( 　　)A．1个　 B．2个 C．3个　 D．4个C 考点专练考点2 等腰三角形的判定例2.将一副直角三角板如图摆放，等腰直角三角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同，且斜边BC与BE在同一直线上，AC与BD交于点O，连接CD.求证：△CDO是等腰三角形．考点专练证明：∵ 在△BDC中，BC＝BD，∴ ∠BDC＝∠BCD.∵ ∠DBE＝30°，∴ ∠BDC＝∠BCD＝75°.∵ ∠ACB＝45°，∴ ∠DOC＝30°＋45°＝75°.∴ ∠DOC＝∠BDC .∴ CD=CO.∴ △CDO是等腰三角形．考点专练考点3 等边三角形的性质例3.如图，已知△ABC是等边三角形，点B，C，D，E在同一直线上，且CG＝CD，DF＝DE，则∠E＝________度。15考点专练考点4 等边三角形的判定例4. 如图，△ABC是等边三角形，与BC边平行的直线分别交AB和AC于点D，E . 求证：△ADE是等边三角形．证明：∵ △ABC是等边三角形，∴ ∠A＝∠B＝∠C＝60°.∵ DE∥BC，∴ ∠B＝∠ADE，∠C＝∠AED ．∴ ∠ADE＝∠AED＝∠A＝60°．∴ △ADE是等边三角形．考点专练考点5 直角三角形例5. 如图，AB∥CD，△EFG的顶点F，G分别落在直线AB，CD上，GE交AB于点H，GE平分∠FGD．若∠EFG＝90°，∠EFH＝20°，求∠EHB的度数．考点专练 考点专练考点6 线段的垂直平分线例6. 如图，E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，垂足分别为C，D，连接CD，交OE于点F.求证：OE是CD的垂直平分线.考点专练证明：∵ E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，∴ DE＝CE.∵OE＝OE，∴ Rt△ODE≌Rt△OCE .∴ OD＝OC.∴ △DOC是等腰三角形．∵ OE是∠AOB的平分线，∴ OE是CD的垂直平分线．考点专练考点7 角平分线的性质与判定例7. 如图，在Rt△ABC中，∠C＝90°，D是AC上一点，DE⊥AB于点E，且DE＝DC.（1）求证：BD平分∠ABC；（2）若∠A＝36°，求∠DBC的度数．考点专练解：(1)∵ DC⊥BC，DE⊥AB，DE＝DC，∴ 点D在∠ABC的平分线上 .∴ BD平分∠ABC.(2)∵∠C＝90°，∠A＝36°，∴∠ABC＝54°.∵BD平分∠ABC，∴∠DBC＝∠ABD＝27°.考点专练考点8 命题和定理例8 .下列四个命题中：①对顶角相等；②如果两条直线被第三条直线所截，那么同位角相等；③如果两个实数的平方相等，那么这两个实数也相等；④当m≠0时，点P（m2，-m）在第四象限内．其中真命题有________（填序号）．①考点专练课程结束