资料中包含下列文件,点击文件名可预览资料内容




当前文件暂不支持在线预览,请下载使用
还剩16页未读,
继续阅读
成套系列资料,整套一键下载
北师大版数学八年级下册 2.2《不等式的基本性质》课件+分层练习(含答案解析)
展开
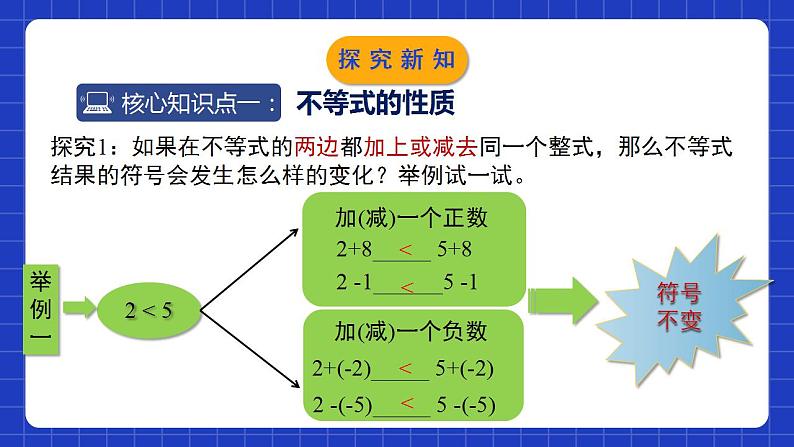
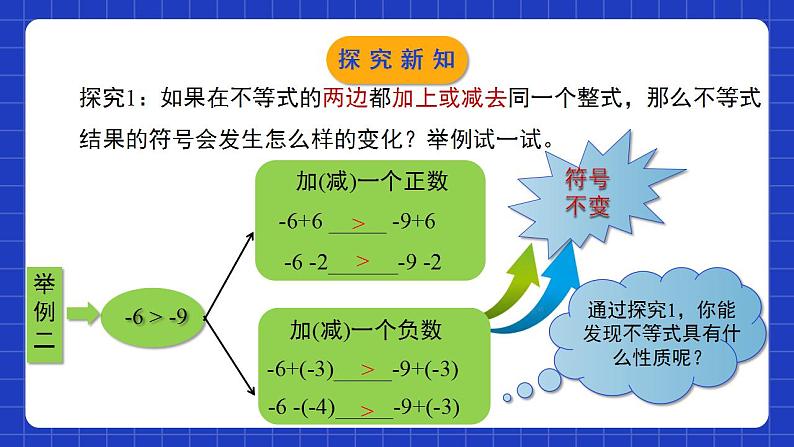
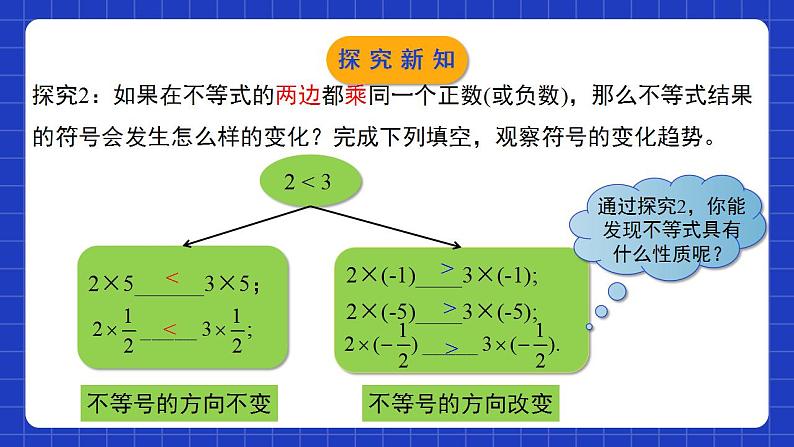
2.2不等式的基本性质学习目标经历不等式的基本性质的探索过程,初步体会不等式和等式的异同;0102掌握不等式的基本性质,并能初步运用不等式的基本性质把比较简单的不等式转化成“x>a”或“x > > > 举例二探究新知归纳总结不等式的基本性质1:不等式的两边都加(或减)同一个整式,不等号的方向不变.用字母表示:若a>b,则a+c >b+c(或a-c >b-c).探究新知<<>>>探究2:如果在不等式的两边都乘同一个正数(或负数),那么不等式结果的符号会发生怎么样的变化?完成下列填空,观察符号的变化趋势。不等号的方向不变不等号的方向改变探究新知<<>>>探究3:如果在不等式的两边都除以同一个正数(或负数),那么不等式结果的符号会发生怎么样的变化?完成下列填空,观察符号的变化趋势。不等号的方向不变不等号的方向改变探究新知不等式的基本性质2 不等式两边都乘(或除以)同一个正数,不等号的方向不变.归纳总结探究新知归纳总结不等式的基本性质3:不等式的两边都乘(或除以)同一个负数,不等号的方向改变.探究新知(1) a - 3____b - 3;(2) a÷3____b÷3(3) 0.1a____0.1b; (4) -4a____-4b(5) 2a+3____2b+3;(6)(m2+1)a____ (m2+1)b(m为常数)>>>>><不等式的性质1不等式的性质2不等式的性质2不等式的性质3不等式的性质1,2不等式的性质2设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.探究新知利用不等式的性质把不等式化成x>a、x<a的形式例:将下列不等式化成“x>a”或“x<a”的形式.(1)x-5>-1;(2)-2x>3x >-1+5即:x > 4;解:(1)根据不等式的基本性质1, 两边都加5,得(3)5x<4x-8探究新知例:将下列不等式化成“x>a”或“x<a”的形式.(1)x-5>-1;(2)-2x>3(3)5x<4x-8(2)根据不等式的基本性质3, 两边都除以-2,得(3)不等式两边同时减去4x得 5x-4x <4x-8-4x, 即x <-8.探究新知注意: 当不等式两边都乘以(或除以)同一个数时,一定要看清是正数还是负数; 对于未给定范围的字母,应分情况讨论。归纳总结探究新知1、已知a,b,c均为实数,a0 B. -3a<-3bC. a|c|n,那么下列结论错误的是( ) A.m+2>n+2 B.m-2>n-2 C.2m>2n D.-2m>-2n D随堂练习B随堂练习4.若 x<y,比较2-3x与2-3y的大小,则下列选项正确的是( ) A. 2-3x>2-3y B .2-3x<2-3y C. 2-3x=2-3y D. 无法比较大小A5.若 3x>-3y,则下列一定成立的是( ) A. x+y>0 B .x-y>0 C.x+y<0 D. x-y<0A随堂练习6.比较大小:(1)如果a-1>b+2,那么a________b.(2)试比较2a与3a的大小:①当a>0时,2a________3a;②当a=0时,2a________3a;③当a<0时,2a________3a.><=>随堂练习7.判断下列各题的推导是否正确?并说明理由.(1)因为a+8>4,所以a>-4;(2)因为4a>4b,所以a>b;(3)因为3>2,所以3a>2a.正确,根据不等式基本性质1.正确,根据不等式基本性质2.不对,应分情况逐一讨论. a>0,a=0,a<0.随堂练习8.试比较a+b与a的大小.9.试判断x2-3x+1与-3x+1的大小.解:∵x2≥0, ∴x2-3x+1≥-3x+1.解:当b>0时,a+b>a; 当b=0时,a+b=a; 当b<0时,a+b<a.随堂练习10.根据不等式的性质,把下列不等式化成x>a或x<a的形式.(1)x+7>9; (2)6x<5x﹣3; (3)
随堂练习不等式的基本性质不等式的基本性质利用不等式的性质把不等式化成“x>a”或“x
相关资料
更多









