北师大版数学八年级下册 3.1.3《图形的平移》第3课时 课件+分层练习（含答案解析）

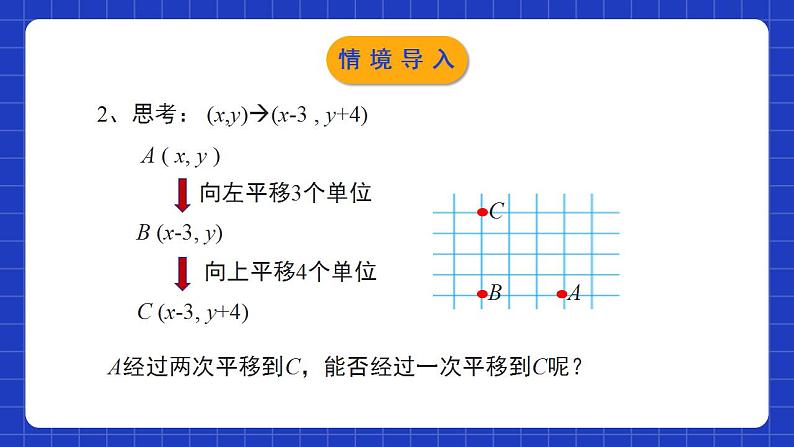
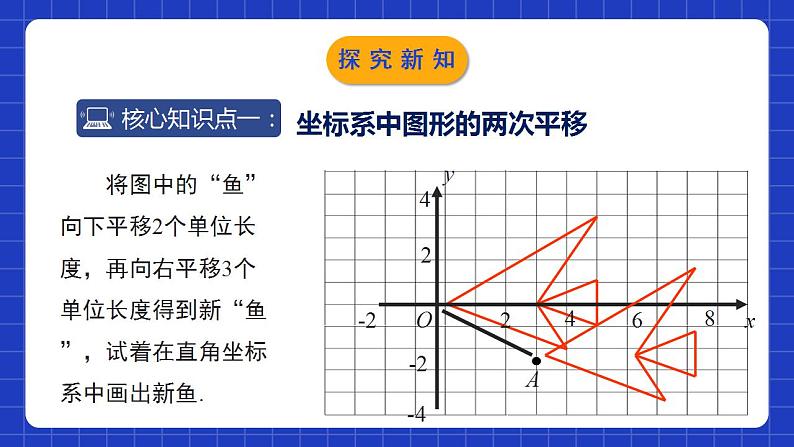
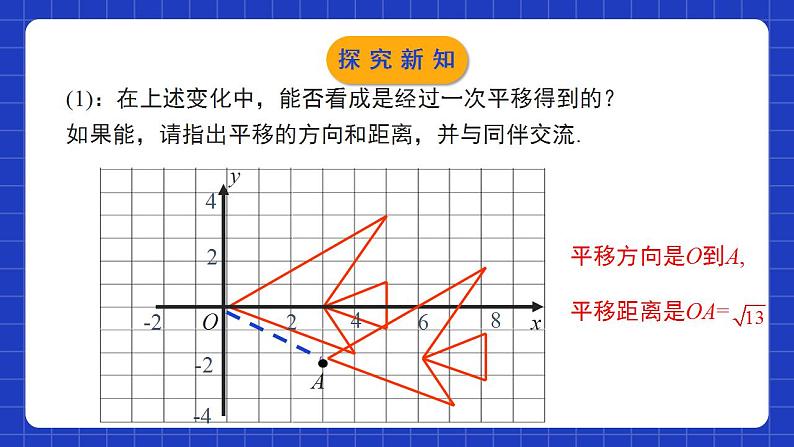
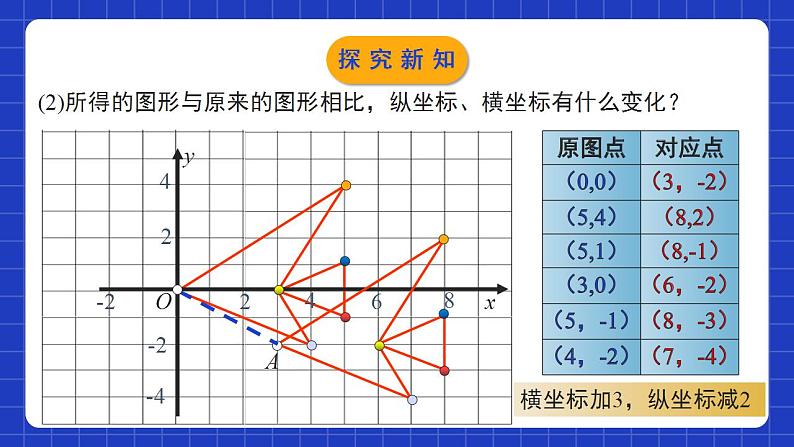
3.1.3图形的平移（第3课时）学习目标理解并掌握图形平移在平面直角坐标系中的变化规律，会利用平移的规律解决两次平移问题．0102经历有关平移的观察、操作、分析及抽象、概括等过程，进一步积累数学活动经验，增强动手实践能力，发展空间观念.（1）(x,y)(x,y＋6)（2）(x,y)(x,y －5)1、在坐标系中，将坐标作如下变化时，图形将怎样变化？向上平移6个单位向下平移5个单位（4）(x,y)(x+3 , y)（3）(x,y) (x-1 , y)向左平移1个单位向右平移3个单位情境导入2、思考： (x,y)(x-3 , y+4)A ( x, y )B (x-3, y)向左平移3个单位向上平移4个单位C (x-3, y+4)ABC A经过两次平移到C，能否经过一次平移到C呢？情境导入坐标系中图形的两次平移 将图中的“鱼”向下平移2个单位长度，再向右平移3个单位长度得到新“鱼”，试着在直角坐标系中画出新鱼.yxO24642-2-4-28A探究新知(1)：在上述变化中，能否看成是经过一次平移得到的？如果能，请指出平移的方向和距离，并与同伴交流.yxO24642-2-4-28A探究新知yxO24642-2-4-28A(2)所得的图形与原来的图形相比，纵坐标、横坐标有什么变化？横坐标加3，纵坐标减2探究新知归纳总结图形平移后，各点坐标的变化规律设(x，y)是原图形上的一点，当它沿x轴方向平移a(a>0)个单位长度、沿y轴方向平移b(b>0)个单位长度后，这个点与其对应点的坐标之间有如下关系：探究新知做一做：先将右图中的“鱼” F的每个“顶点” 的横坐标分别加2,纵坐标不变,得到 “鱼” G；再将“鱼” G的每个“顶点” 的纵坐标分别加3，横坐标不变，得到“鱼” H.“鱼” H与原来的 “鱼” F相比有什么变化？能否将“鱼” H看成是“鱼” F经过一次平移得到的？与同伴交流.探究新知yxFGH6探究新知归纳总结探究坐标变化后，图形的变化规律 设(x，y)是原图形上的一点，横坐标增加或减少a(a>0)、纵坐标增加或减少b(b>0)后，平移后的图形与原图形之间的位置有如下关系：探究新知归纳总结两次平移所得图形的坐标变化(1)遵循上加下减,左减右加的平移规律.(2)对应点连线的方向就是图形平移的方向,对应点连线的线段长度就是平移的距离.探究新知原图形上点P（x,y)平移后图形上点P（x±a,y±b)图形沿x轴方向平移a个单位长度图形沿y轴方向平移b个单位长度平移的方向：从原图形上一点到其对应点的方向.平移的距离：将一个图形沿着x轴方向平移a(a＞0）个单位长度；再严重y轴方向平移b个单位长度，平移前后图形对应点的坐标关系探究新知例：四边形ABCD各顶点的坐标分别为A(-3,5)，B(-4,3)，C(-1,1)，D(-1,4)，将四边形ABCD先向上平移3个单位长度，再向右平移4个单位长度，得到四边形A′B′C′D′.探究新知（1）四边形A′B′C′D′与四边形ABCD对应点的横坐标有什么关系？纵坐标呢？分别写出点A′，B′，C′，D′的坐标；解：四边形A′B′C′D′与四边形ABCD对应点的横坐标分别增加了4，纵坐标分别增加了3，A′（1，8），B′（0，6），C′（3，4），D′（3，7）.探究新知（2）如果四边形A′B′C′D′看成是由四边形ABCD经过一次平移得到的，请指出这一平移的平移方向和平移距离.解：平移方向A到A′，如图所示；平移距离AA',由勾股定理得AA'=5.探究新知1.在平面直角坐标系中，将点A（1，﹣2）向上平移3个单位长度，再向左平移2个单位长度，得到点A′，则点A′的坐标是（　　 ）A.（﹣1，1） B. （﹣1，﹣2） C. （﹣1，2） D. （1，2）A随堂练习2.在平面直角坐标系内,线段CD是由线段AB平移得到的A(-2,3)的对应点为点C(2,-2),则点B(-4,1)的对应点D的坐标为(　 　)A.(-6,-4)　　 B.(-4,0)C.(6,-4)　 D.(0,-4)D随堂练习3.下面所说的“平移”,是指只沿方格的格线(即左右或上下)运动,并将图中的任意一条线段平移一格称为“1步”.通过平移,使得图中的3条线段首尾相接组成一个三角形,最少需要移动的步数是(　 　)A.7步 B.8步 C.9步 D.10步B随堂练习4.在如图所示的直角坐标系中,△ABC经过平移后得到△A1B1C1(两个三角形的顶点都在格点上),已知在AC上一点P(2.4,2)平移后的对应点为P1,则P1点的坐标为 (　 　)CA.(-0.4,-1) B.(-1.5,-1)C.(-1.6,-1) D.(-2.4,-2)随堂练习5.如图,△ABC各顶点的坐标分别为A(-2,6)，B(-3,2)，C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.(1)分别写出△DEF各顶点的坐标.解:∵A(-2,6),B(-3,2),C(0,3),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,得到△DEF.∴D(2,9),E(1,5),F(4,6).随堂练习(2)如果将△DEF看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.解:连接AD,∵由图可知,AD= =5,∴如果将△DEF看成是由△ABC经过一次平移得到的,那么这一平移的平移方向是由A到D的方向,平移的距离是5个单位长度.随堂练习1.横坐标分别增加(减少)a(a＞0)，纵坐标分别增加(减少)b(b＞0)：图形向右(向左)平移a个单位长度，再向上(向下)b平移个单位长度．2.图形向右(向左)平移a(a＞0)个单位长度，再向上(向下)平移b(b＞0)个单位长度：原坐标(x，y)变为(x±a，y±b)．课堂小结课程结束