



所属成套资源:北师大版数学初二下学期课件PPT+分层练习(含答案解析)+单元小结课件+单元测试全套
北师大版数学八年级下册 4.3.1 《公式法》第1课时 课件+分层练习(含答案解析)
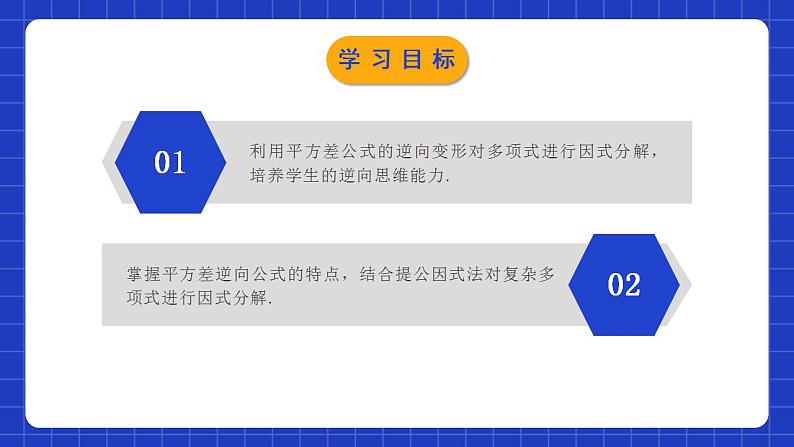
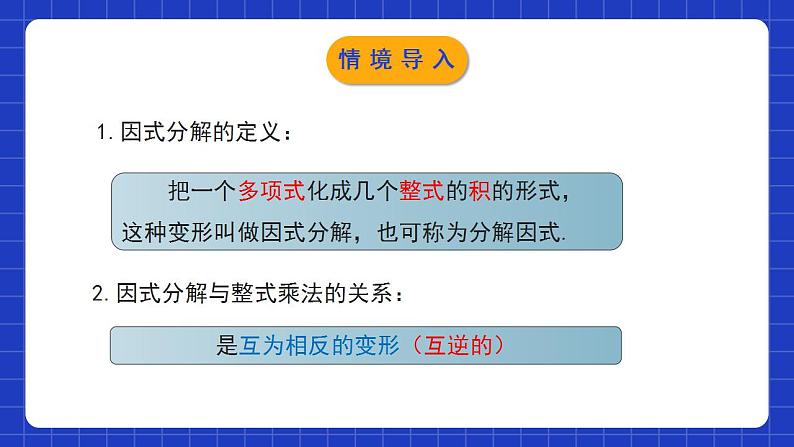
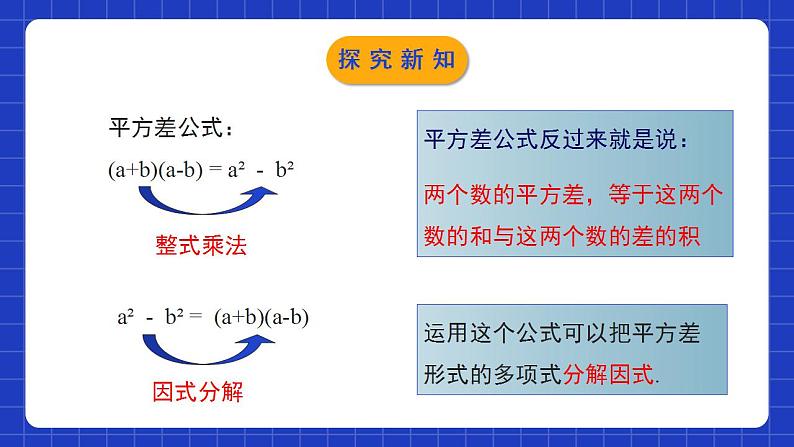
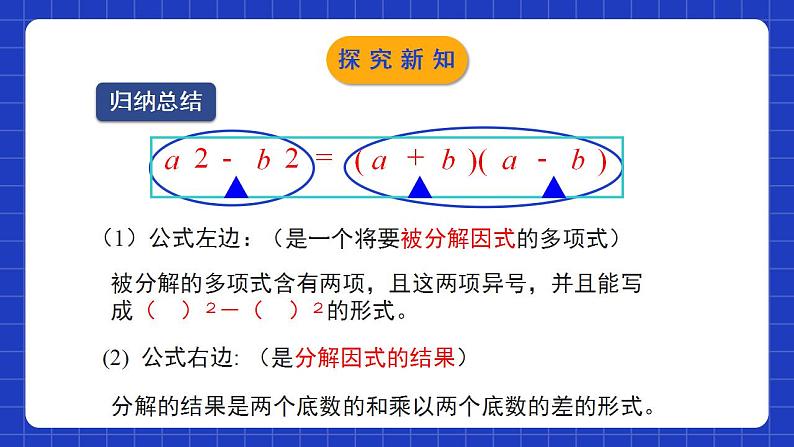
展开4.3.1公式法(第1课时)学习目标利用平方差公式的逆向变形对多项式进行因式分解,培养学生的逆向思维能力.0102掌握平方差逆向公式的特点,结合提公因式法对复杂多项式进行因式分解.1.因式分解的定义:2.因式分解与整式乘法的关系:是互为相反的变形(互逆的)情境导入3.提公因式法:情境导入用平方差公式进行因式分解问题1:观察多项式x2-25,9x2-y2,它们有什么共同的特征?因为多项式x2-25,9x2-y2,可分别化为x2-52和(3x)2-y2的形式,所以它们的共同特征是:都是两个数平方差的形式.探究新知问题2:尝试将它们分别写成两个因式的乘积,并与同伴交流.多项式x2-25,9x2-y2的共同特征都是两项,且都是差的形式,各项都能写成平方的形式:x2-25=x2-52=(x+5)(x-5);9x2-y2=(3x)2-y2=(3x+y)(3x-y).探究新知平方差公式反过来就是说:两个数的平方差,等于这两个数的和与这两个数的差的积a² - b² = (a+b)(a-b)因式分解平方差公式:(a+b)(a-b) = a² - b²整式乘法运用这个公式可以把平方差形式的多项式分解因式.探究新知归纳总结(1)公式左边:(是一个将要被分解因式的多项式)被分解的多项式含有两项,且这两项异号,并且能写成( )2-( )2的形式。(2) 公式右边:(是分解因式的结果)分解的结果是两个底数的和乘以两个底数的差的形式。探究新知例1:利用平方差公式分解因式: (1)16m2–9n2 (2)16–x2y2 (3)25a2– (4)–9+x2法1:互换位置原式=x2-9 =(x+3)(x-3)法2:提取负号原式= -(9-x2) = - (3+x)(3-x)探究新知例2:把下列各式分解因式 (1) (2)-169y2y2解:(1)原式=( )2-( )292y232y3交换位置探究新知(x+q)(x+p)想一想:多项式 (x+p) 2 - (x+q) 2能用平方差公式分解因式吗? =(x+p+x+q)×(x+p-x-q) =(2x+p+q)(p-q)解:原式=[( )+( )]×[( )-( )]整体思想x+qx+px+qx+p探究新知例3:把下列各式分解因式 (1) 9(x–y)2–(x+y)2 (2) 解:原式=[3(x-y)] 2-(x+y) 2=[3(x-y)+(x+y)][3(x-y)-(x+y)]=(3x-3y+x+y)(3x-3y-x-y)=(4x-2y)(2x-4y)=2(2x-y)×2(x-2y)=4(2x-y)(x-2y)原式=(a-b) 2-[4(a+b)] 2=[(a-b)+4(a+b)][(a-b)-4(a+b)]=(a-b +4a+4b) (a-b -4a-4b)=(5a+3b)(-3a-5b)=-(5a+3b)(3a+5b)探究新知解:原式=2x(x2-4)=2x(x2-22)=2x(x+2)(x-2)解:原式=3xy(x2-4) =3xy(x2-22) =3xy(x+2)(x-2)解:原式=3a(x2-y4) =3a[x2-(y2)2] =3a(x+y2)(x-y2)解:原式=32-2(m-n)2 =2[16-(m-n)2] =2[42-(m-n)2] = 2[4+(m-n)][4-(m-n)] = 2(4+m-n)(4-m+n)探究新知因式分解的一般步骤:1、如果多项式的各项含有公因式,那么应先提取公因式;2、如果多项式的各项不含有公因式,那么可以尝试运用公式法因式分解(即平方差公式和完全平方公式);3、如果上述方法都不能进行因式分解,那么可以先整理多项式,然后分解;4、因式分解必须分解到每一个因式都不能再分解为止。遵循“一提、二套、三检查”的原则归纳总结探究新知 BC随堂练习3. -4+0.09a2因式分解的结果是( )A.(0.3a+2)(0.3a-2) B.(2+0.3a)(2-0.3a)C.(0.03a+2)(0.03a-2) D.(2+0.03a)(2-0.03a)A随堂练习4.因式分解.(1)x2-y2= . (2)x2-9= . (3)x5-x3= . (4)a3-ab2= . 5.计算:552-452= . (x+y)(x-y) (x+3)(x-3) x3(x+1)(x-1) a(a+b)(a-b) 1 000 随堂练习6.因式分解(1)4a2-9b2.(2)-4x2+9.(3) 4ax2-4a.(4)(x2+y2)2-x2y2.解:原式=(2a)2-(3b)2=(2a+3b)(2a-3b)解:原式=32-(2x)2=(3+2x)(3-2x)解:原式=4a(x2-1)= 4a(x+1)(x-1)解:原式=(x2+y2)2-(xy)2=(x2+y2+xy)(x2+y2-xy)随堂练习7.用简便方法计算。(1)81.52-78.52. (2) 5×7.282-5×2.722.解:原式=(81.5+78.5)×(81.5-78.5)=160×3=480解:原式=5×(7.28+2.72)×(7.28-2.72)=5×10×4.56=228随堂练习8.因式分解.(1) x4-y4;(2) 16(a-1)2-9(b+2)2. 解:原式=(x2+y2)(x2-y2)=(x2+y2)(x+y)(x-y)随堂练习一、利用平方差公式的逆向变形对多项式的因式分解.a2-b2=(a+b)(a-b).1.注意多项式的形式是否符合两个数或式的平方差的形式; 2.因式分解过程中或分解后可能要进行整式的乘法运算 3.当多项式的各项含有公因式时,通常先提公因式,如何再进一步因式分解. 二、利用平方差公式的逆向变形分解因式的注意事项课堂小结课程结束







