北师大版数学九年级下册 2.2.2 《二次函数的图象与性质》第2课时 课件+分层练习（含答案解析）

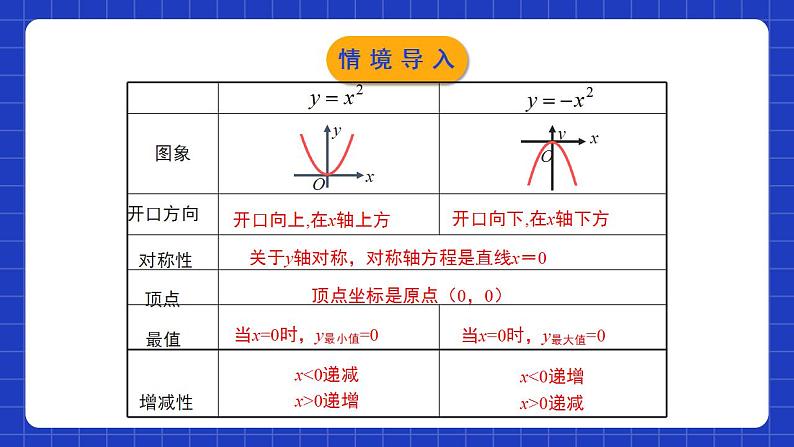
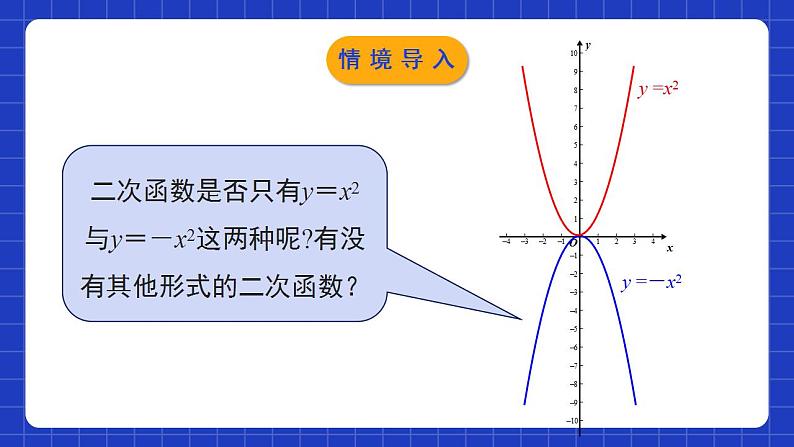
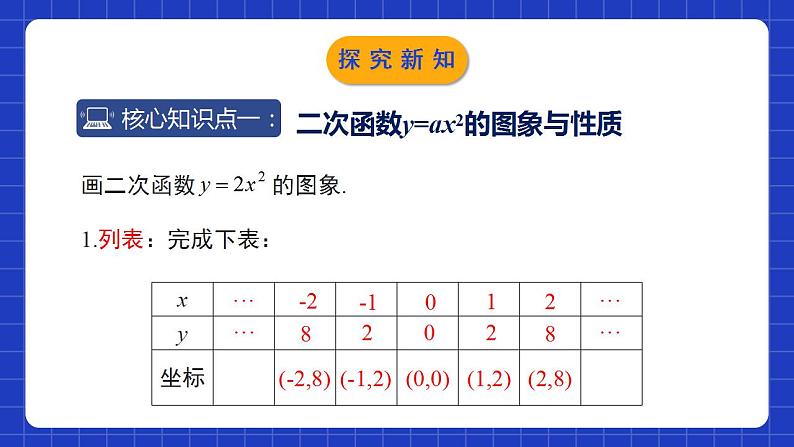
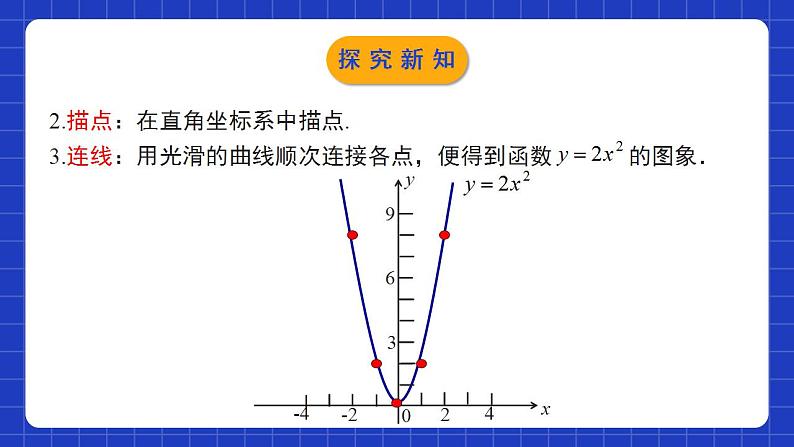
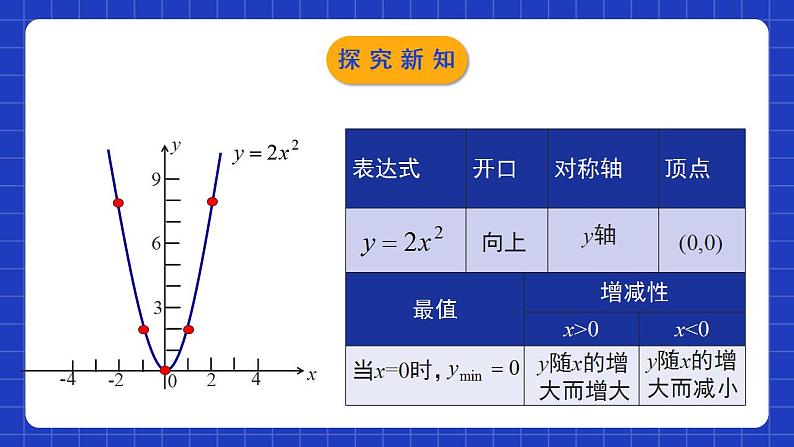
2.2.2二次函数的图象与性质第2课时学习目标比较函数y=ax2与y=ax2+c的联系.会画二次函数y=ax2和y=ax2+c的图象.掌握二次函数y=ax2和y=ax2+c的性质并会应用.开口方向对称性顶点增减性开口向上,在x轴上方开口向下,在x轴下方关于y轴对称，对称轴方程是直线x＝0顶点坐标是原点（0，0）当x=0时，y最小值=0当x=0时，y最大值=0x0递增x0递减最值情境导入二次函数是否只有y＝x2与y＝－x2这两种呢?有没有其他形式的二次函数？情境导入二次函数y=ax2的图象与性质1.列表：完成下表：-28-12001228(-2,8)(-1,2)(0,0)(1,2)(2,8)············探究新知2.描点：在直角坐标系中描点.探究新知向上y轴(0,0)当x=0时，y随x的增大而增大y随x的增大而减小探究新知y =x2①列表；②描点；③连线.y=2x2探究新知y =x2y=2x2开口都向上，对称轴都是y轴.顶点都是原点(0，0)，顶点是抛物线的最低点.当x0时，y随x增大而增大.y=2x2抛物线的开口最小．探究新知y =－x2①列表；②描点；③连线.y=-2x2探究新知y =－x2y=-2x2 函数 ，y=－2x2的图象与函数y=－x2的图象相比，有什么共同点和不同点？开口都向下；对称轴都是y轴.顶点都是原点(0，0)，顶点是抛物线的最高点；当x0时，y随x增大而减小.a值越小，抛物线的开口越小．探究新知归纳总结向上向下(0，0)(0，0)y轴 (x=0)y轴 (x=0)在对称轴的左侧，y随着x的增大而减小.在对称轴的右侧，y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧，y随着x的增大而减小.x=0时，y最小=0x=0时，y最大=0抛物线y=ax2 (a≠0)的形状是由|a|来确定的，一般说来，|a|越大，抛物线的开口就越小.探究新知二次函数y=ax2+c的图象与性质2.它是轴对称图形吗？它的开口方向、对称轴、顶点坐标分别是什么呢？形状相同，位置不同探究新知向上平移一个单位长度向下平移一个单位长度探究新知向上y轴(0,0)y随x的增大而增大y随x的增大而减小向上y轴(0,1)y随x的增大而增大y随x的增大而减小向上y轴(0,-1)y随x的增大而增大y随x的增大而减小探究新知二次函数 与 的图象的关系：二次函数 的图象可以由 的图象平移得到：当c > 0时,向上平移c个单位长度得到.当c < 0时,向下平移 |c|个单位长度得到.向上y轴(0,c)y随x的增大而增大y随x的增大而减小向下y轴(0,c)y随x的增大而减小y随x的增大而增大归纳总结探究新知D随堂练习2. 函数y＝k(x－k)与y＝kx2，y＝ (k≠0)在同一平面直角坐标系中的图象可能是(　　)C随堂练习D随堂练习上3下1向下y轴(0，-5)随堂练习5.已知点(－7，y1)，(3，y2)，(－1，y3)都在抛物线y＝ax2＋k(a＞0)上，则(　　) A．y1＜y2＜y3　 B．y1＜y3＜y2 　 C．y3＜y2＜y1　 D．y2＜y1＜y3分析：∵抛物线y＝ax2＋k(a＞0)关于y轴对称，且点(3，y2) 在抛物线上，∴点(－3，y2)也在抛物线上．∵(－7，y1)，(－3，y2)，(－1，y3)三点都在对称轴左侧，在y轴左侧时，y随x的增大而减小，且－7＜－3＜－1，∴y3＜y2＜y1.C随堂练习随堂练习二次函数y=ax2+c（a≠0)的图象和性质图象性质与y=ax2的关系开口方向由a的符号决定；c决定顶点位置；对称轴是y轴.增减性结合开口方向和对称轴才能确定.平移规律：c正向上；c负向下.课堂小结课程结束