北师大版数学九年级下册 3.3 《垂径定理》课件+分层练习（含答案解析）

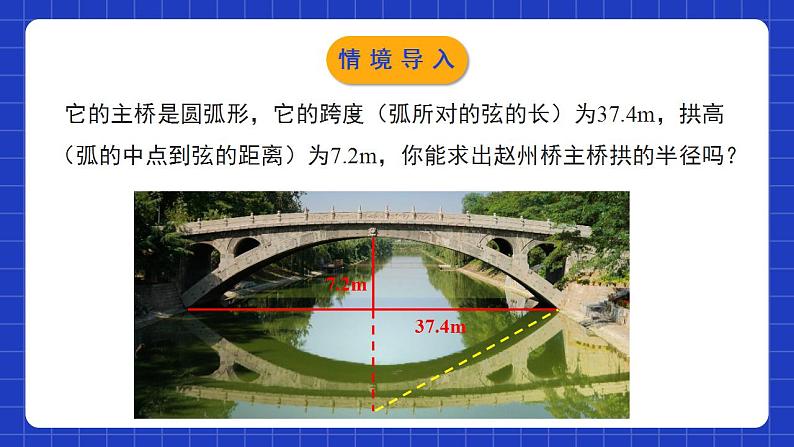
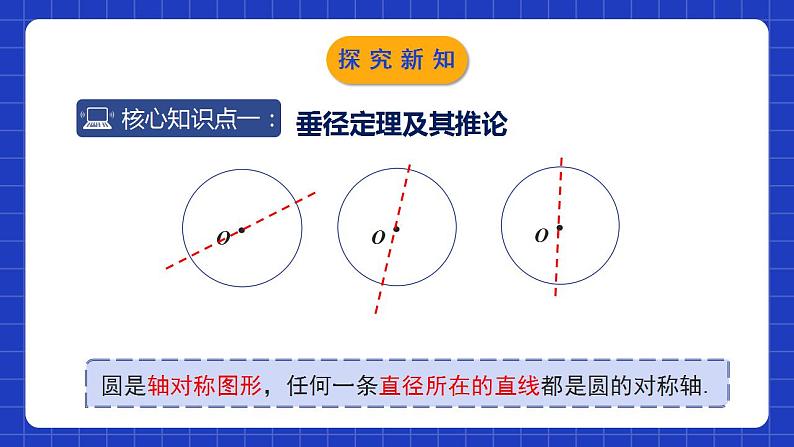
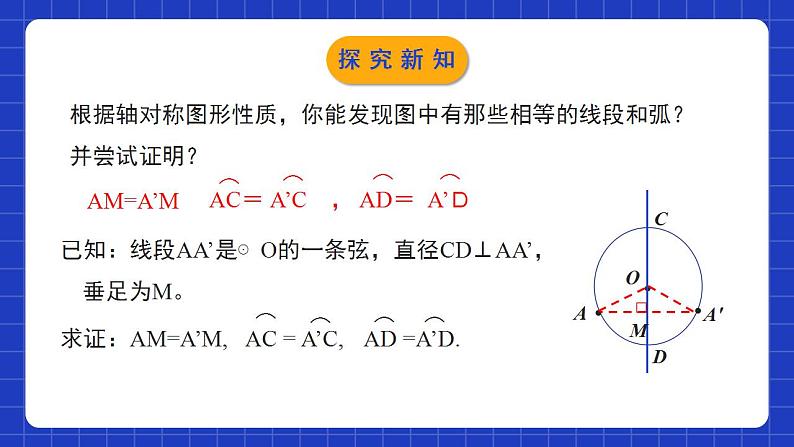
3.3垂径定理学习目标理解垂径定理的推导。利用垂径定理解决实际问题。你知道赵州桥吗？它是1300多年前我国隋代建造的石拱桥，是我国古代人民勤劳与智慧的结晶．情境导入它的主桥是圆弧形，它的跨度（弧所对的弦的长）为37.4m，拱高（弧的中点到弦的距离）为7.2m，你能求出赵州桥主桥拱的半径吗？37.4m7.2m情境导入垂径定理及其推论圆是轴对称图形，任何一条直径所在的直线都是圆的对称轴.探究新知根据轴对称图形性质，你能发现图中有那些相等的线段和弧？并尝试证明？AM=A’M探究新知证明:设CD是⊙O的任意一条直径，A为⊙O上的点CD以外的任意一点. 过A作AA'垂直CD，交于⊙O点A'，垂足为M，连接OA，OA'.在△OAA'中，∵OA=OA'，∴△OAA'是等腰三角形.又∵AA'垂直CD∴MA=MA'即CD是AA'的垂直平分线.探究新知从上面的证明过程中我们可以知道：探究新知归纳总结垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧．用几何语言表述为：如图，在⊙O中，探究新知垂径定理的几个基本图形：探究新知练一练：判断下列图形，能否使用垂径定理？定理中的两个条件缺一不可——直径（半径），垂直于弦探究新知如图，AB是⊙O的弦(不是直径)，作一条平分AB的直径CD，交AB于点M（1）图是轴对称图形吗?如果是其对称轴是什么？（2）你能发现图中有哪些等量关系？说一说你的理由.探究新知连接OA、OB，易证OM⊥AB，∠AOC=∠BOC探究新知归纳总结垂径定理推论：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的弧。符号语言：在⊙O中，∵CD是直径，AM=BM，且AB不是直径，∴CD⊥AB，探究新知根据垂径定理与推论可知对于一个圆和一条直线来说，如果具备（1）过圆心；（2）垂直于弦；（3）平分弦；（4）平分弦所对的优弧；（5）平分弦所对的劣弧.上述五个条件中的任何两个条件都可以推出其他三个结论.归纳总结探究新知例：如图, 一条公路的转弯处是一段圆弧（即 图中 ,点O是 所在圆的圆心），其中CD= 600m， E为 上一点，且OE丄CD，垂足为F，EF=90m.求这段弯路的半径.└探究新知解:连接OC.设这段弯路的半径为Rm,则OF=(R-90)m.根据勾股定理，得解得R=545.∴这段弯路的半径约为545m.探究新知试一试：1 400年前，我国隋朝建造的赵州石拱桥的桥拱是圆弧形，它的跨度（即弧所对的弦长）为37.4 m，拱高（即弧的中点到弦的距离）为7.2 m，求桥拱所在圆的半径（结果精确到0.1 m）.探究新知解：如图，OD = OC – DC = R – 7.2 .在 Rt△AOD 中，由勾股定理，得OA2 = AD2 + OD2 ，即 R2 = 18.72 +（R – 7.2）2解得 R ≈ 27.9（m）.答：赵州桥的主桥拱半径约为27.9m.AB = 37.4，CD = 7.2探究新知1.已知⊙0的半径为13cm，弦AB的长为10cm，则圆心到弦AB的距离为( ) A. 8cm B. 5cm C. 9cm D. 12cmBADD随堂练习2.如图，AB 是⊙O 的直径，弦 CD⊥AB，垂足为 M，下列结 论不一定成立的是（ ）CM = DM B. C. ∠ACD =∠ADC D. OM = MDD 随堂练习3.如图AB是⊙O的直径，C是⊙O上的一点,若BC=6, AB=10, OD⊥BC于点D,则OD的长为______4随堂练习4. “圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材，埋在壁中，不知大小.以锯锯之，深一寸，锯道长一尺.问:径几何?”转化为现在的数学语言就是:如图，CD为⊙О的直径，弦AB⊥CD，垂足为E，CE=1寸，AB=10寸，求直径CD的长.随堂练习随堂练习5.如图，两个圆都以点O为圆心，小圆的弦CD与大圆的弦AB在同一条直线上，你认为AC与BD的大小有什么关系？为什么？解：AC=BD.理由如下:如图所示,过点О作OE⊥AB于点E.∵在大圆中,AE=EB,在小圆中,CE=ED,∴AE-CE=EB-ED,即AC=BD.随堂练习垂直于弦的直径垂弦定理的推论垂弦定理垂直于弦的直径平分弦,并且平分弦所对的两条弧.平分弦（不是直径）的直径垂直于弦,并且平分弦所对的弧.课堂小结课程结束