




初中北师大版1 圆一等奖课件ppt
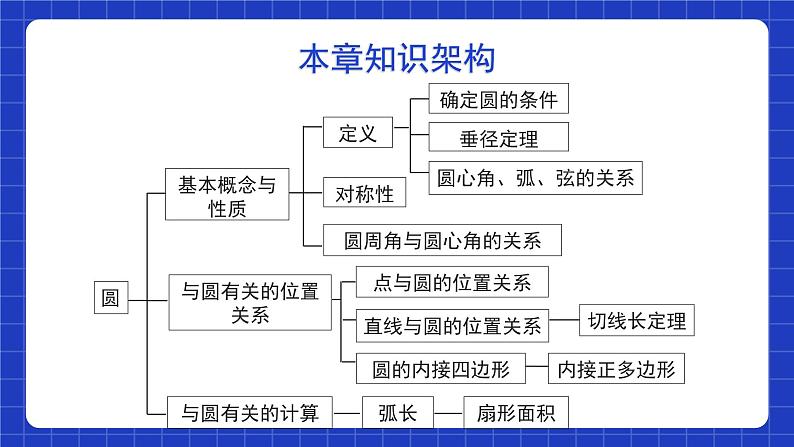
展开一、圆的基本概念及其性质
1. 定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆.其中定点称为______,定长称为半径.如图,以点O为圆心的圆记作⊙O,线段OA叫做半径.
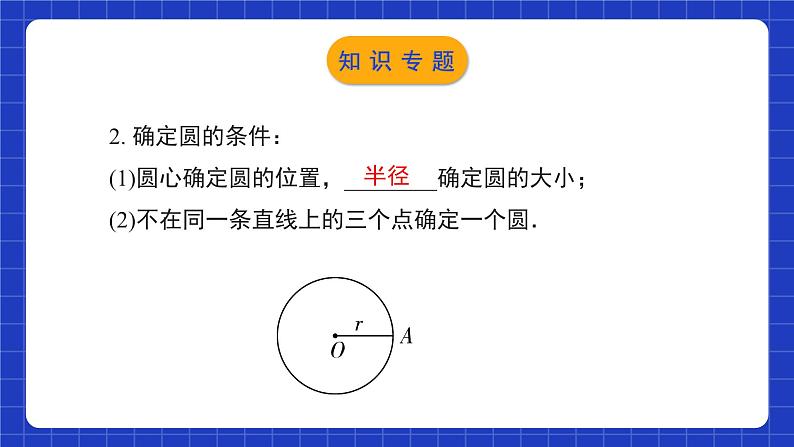
2. 确定圆的条件:(1)圆心确定圆的位置,________确定圆的大小;(2)不在同一条直线上的三个点确定一个圆.
(1)圆既是轴对称图形又是中心对称图形,对称轴是任意一条____ 所在的直线,对称中心是________。(2)圆具有旋转不变形,及圆围绕着它的圆心旋转任意角度都能与原来的图形重合。
4. 与圆有关的概念:(1)弦:连接圆上任意两点的________叫做弦,如AC、BC;(2)直径:经过________的弦叫做直径,直径等于半径的2倍;(3)弧:圆上任意两点间的部分叫做圆弧,简称弧,大于半圆的弧叫做______,如弧ABC,小于半圆的弧叫做______,如AB,BC,AC ;
(4)半圆:圆上任意一条直径的两个端点分圆成____条弧,每一条弧都叫半圆;(5)等圆:能够______的两个圆叫做等圆; (6)等弧:在____________中,能够互相重合的弧叫做等弧;
温馨提示:等弧只存在同圆或等圆中,大小不等的圆中不存在等弧
(7)圆周角:顶点在圆上,并且两边都与圆相交的角叫做圆周角,如∠ACB; (8)圆心角:顶点在________的角叫做圆心角,如∠AOB; (9)弦心距:圆心到弦的距离叫做弦心距,如OD.
(10)圆内接四边形:四边形的__________都在圆上,像这样的四边形叫做圆内接四边形。
1. 定理:在同圆或等圆中,相等的圆心角所对的弧____,所对的弦也______;
二、 弦、弧、圆心角的关系
2. 推论:(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角______,所对的弦______; 符号语言:
(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角______,所对的优弧与劣弧分别______;
注意:(1)理解圆心角、弧、弦三者之间的关系时,必须在同圆或等圆中:①一条弦对着两条弧,优弧和劣弧;②等弧和同弧所对应的圆周角有无数个,注意它们之间的相互转化.(2)在同圆或等圆中,两个圆心角、两条弦、两条弧中如果有一组量相等,则它们所对应的其余各组量也分别相等.
2. 推论(1)同弧或等弧所对的圆周角______;如图,在⊙O中,∠A和____是 所对的圆周角⇒∠A=____; ⇒ ∠A=______;
(2)半圆(或直径)所对的圆周角是___________,90°的圆周角所对的弦是______;如图,在⊙O中,AB是直径⇒∠ACB=______.
三、 圆周角定理及其推论
1. 定理:一条弧所对的圆周角等于它所对的圆心角的________.
3. 圆周角定理的几种基本图形及结论:
注意:在遇到与直径有关的问题时,一般要构造直径所对的圆周角,由直径转化出直角.
1. 定理:垂直于弦的直径______弦,并且______弦所对的两条弧;
∵在⊙O中,CD⊥ABCD是直径
四、 垂径定理及其推论
2. 推论:平分弦(不是直径)的直径______于弦,并且______弦所对的两条弧;
∵在⊙O中,AM=BMCD是直径
五、角形的外接圆及其性质
【知识拓展】如图,a、b是Rt△ABC的直角边,c为斜边,则:①外接圆圆心为AB边的中点;②外接圆半径R=
六、圆内接四边形及其性质
1. 概念:四边形的四个顶点均在同一个圆上的四边形叫做圆的内接四边形.2. 性质:(1)圆内接四边形的对角________;如图,∠A+∠BCD=180°,∠B+∠D=180°;(2)圆内接四边形的任意一个角的外角等于它的内对角,如图,∠DCE=______.
考点一 与圆有关的性质
【要点指导】垂径定理及其推论是证明两线段相等、两条弧相等及两直 线垂直的重要依据之一. 在有关弦长的计算中常常需要添加辅助线构造直角三 角形, 使问题得以突破与解决. 在解决与圆有关的角度问题时, 应注意圆心角、 圆周角之间的相互转化. 当涉及弦(非直径)所对的弧时应分两种情况:弦(非直 径)所对的弧可能是优弧, 也可能是劣弧.
考点二 切线的判定和性质的综合应用
分析: (1)因为CA=CB, 所以考虑连接 OC, 由垂径定理的推论得出OC⊥AB, 进而由CD∥AB证得OC⊥CD. (2)在 △ODC中, 由边角关系易得CD的长.
【要点指导】 (1)证明切线时通常运用下面两种方法: ①若已知直线和圆有公共点, 通常可作出经过该点的半径, 然后证明这条半径和已知直线垂直; ②若未明确说明已知直线和圆是否有公共点, 通常过圆心作这条直线的垂线段, 然后证明这条垂线段的长等于半径. (2)运用切线的性质时常作过切点的半径解决问题.
考点三 与圆有关的计算
【要点指导】解决与圆有关的正多边形的计算问题的关键在于适当添加辅助线构造直角三角形,再运用勾股定理来解决问题. 要熟记弧长、扇形 面积的计算公式, 这部分试题常与相关的数学元素、生活情境等结合;求与 圆相关的不规则图形的面积, 一般情况下, 都要借助于圆的有关性质, 并与其他知识相结合, 间接求解.
初中数学北师大版九年级下册1 二次函数精品课件ppt: 这是一份初中数学北师大版九年级下册<a href="/sx/tb_c102698_t3/?tag_id=26" target="_blank">1 二次函数精品课件ppt</a>,共31页。PPT课件主要包含了二次函数,相关概念,抛物线,对称轴,性质和图象,增减性,解析式的确定,本章知识架构,知识专题,x0y轴等内容,欢迎下载使用。
初中数学北师大版九年级下册第三章 圆1 圆教学课件ppt: 这是一份初中数学北师大版九年级下册第三章 圆1 圆教学课件ppt,文件包含北师大版初中数学九年级下册第三章圆单元小结同步课件pptx、北师大版初中数学九年级下册第三章圆单元小结教学设计含教学反思docx等2份课件配套教学资源,其中PPT共31页, 欢迎下载使用。
北师大版九年级下册1 圆课堂教学课件ppt: 这是一份北师大版九年级下册1 圆课堂教学课件ppt,共28页。PPT课件主要包含了投圈游戏,圆的定义,你能帮老师想想办法吗,与圆有关的概念,劣弧与优弧,圆心角,点与圆的位置关系,练习拓展等内容,欢迎下载使用。