资料中包含下列文件,点击文件名可预览资料内容






当前文件暂不支持在线预览,请下载使用
还剩17页未读,
继续阅读
所属成套资源:【新课标】北师大版数学七年级下学期PPT课件+分层练习(含答案解析)+单元小结+单元测试整册
成套系列资料,整套一键下载
北师大版数学七年级下册 1.1《同底数幂的乘法》课件+分层练习(含答案解析)
展开
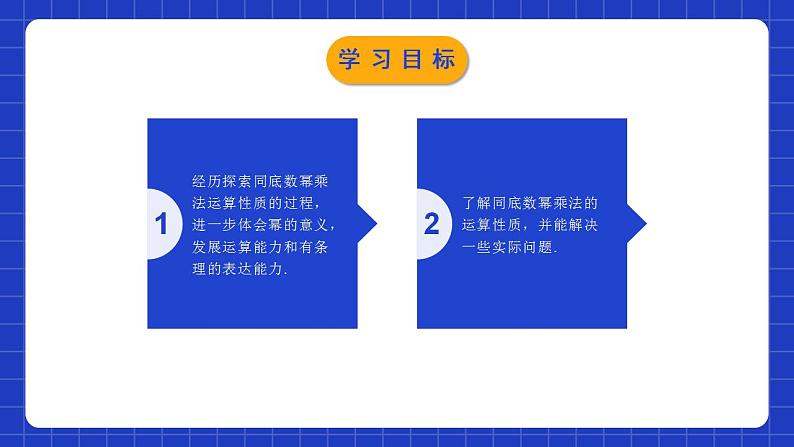
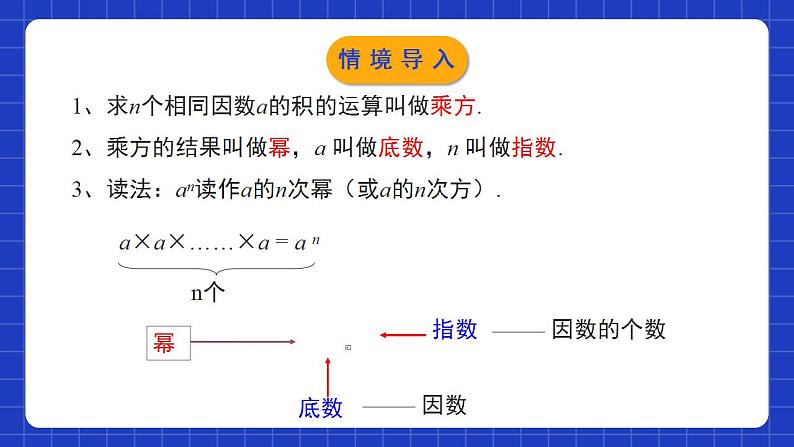
1.1同底数幂的乘法学习目标1经历探索同底数幂乘法运算性质的过程,进一步体会幂的意义,发展运算能力和有条理的表达能力.2了解同底数幂乘法的运算性质,并能解决一些实际问题.1、求n个相同因数a的积的运算叫做乘方.2、乘方的结果叫做幂,a 叫做底数,n 叫做指数.3、读法:an读作a的n次幂(或a的n次方). 情境导入 由我国中科院软件所和清华大学共同研制的“神舟·太湖之光”在最新一期的全球超级计算机500强中位列第三位,速度达到每秒9.3亿亿(9.3×1016)次运算.问:它工作一年可以进行多少次运算?(一年以3×107秒计算)(9.3×1016)×(3×107)情境导入同底数幂相乘(9.3×1016)×(3×107) 思考:该怎么计算呢?通过观察,你发现了1016和107有什么共同的特点了吗? 我们观察可以发现,1016和107这两个幂的底数相同,是同底的幂的形式. 所以我们把1016×107这种运算叫做同底数幂的乘法. 探究新知(1)25×22=2 ( )做一做:1.根据乘方的意义填空,观察计算结果,你能发现什么规律?=(2×2×2×2×2)×(2×2)=2×2×2×2×2× 2×2=27(2)a3·a2=a( )=(a﹒a﹒a) (a﹒a)=a﹒a﹒a﹒a﹒a=a575探究新知 5m× 5n =5( ?)2.根据乘方的意义填空,观察计算结果,你能发现什么规律?=(5×5×5×…×5)(m个5)×(5×5×5 ×…×5)(n个5)=5×5×…×5(m+n个5)=5m+n探究新知如果 m,n 都是正整数,那么 am·an 等于什么?为什么?am·an( 个a)·(a·a·…·a)( 个a)=(a·a·…·a)( 个a)=a( ) (乘方的意义)(乘法的结合律)(乘方的意义)mn m+n m+n =(a·a·…·a)探究新知归纳总结同底数幂的乘法的运算性质:注意:底数a可以是单项式或多项式,但指数必须是正整数。m+n 指数相加底数不变同底数幂相乘,底数不变,指数相加探究新知例1 计算:(1)(–3)7×(–3)6 ; (2) ;(4) b2m·b2m+1 .(3) –x3·x5;解:探究新知注意:1.公式中的底数和指数可以是一个数、字母或一个式子.2.计算同底数幂的乘法时,要注意算式里面的负号是属于幂的还是属于底数的.归纳总结探究新知想一想:当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?用字母表示am· an·ap 等于什么呢?am· an·ap=(am· an)·ap=am+n·ap=am+n+p(m,p,n都是正整数)这一性质可以推广到多个同底数幂相乘的情况:am · an......ap=am +n+.......P(m,p,n都是正整数)探究新知例2:计算: (1) (-b)3·b·(-b)2 (2) (x-2)2·(x-2)3+(x-2)2·(2-x)3(1)解:原式=-b3bb2 =-b3+1+2 =-b6(2)解:原式=(x-2)2+3-(x-2)2+3 =(x-2)5-(x-2)5 =0底数不相同要转化为同底数幂相乘。探究新知例3:(1)已知a2=m,a3=n 求a5(2)已知4×22m=16,求(m-2)2021-m解:(1)a5=a2a3=mn (2)4×22m=22×22m=22+2m=24 ∴2+2m=4 ∴ m=1 (m-2)2021-m =(1-2)2021-1 =1同底数幂的乘法法则的逆应用am+n=am·an(m、n都是正整数)探究新知例4: 计算:(1)(x-y )2 • (x-y ) • (x-y )5;(2)(a+b)2 • (a+b)5;(3)(x+3)3 • (x+3)5 • (x+3).解:(1)(x-y )2·(x-y )·(x-y )5=(x-y )2+1+5=(x-y )8;(2)(a+b)2·(a+b)5=(a+b)2+5=(a+b)7;(3)(x+3)3·(x+3)5·(x+3)=(x+3)3+5+1=(x+3)9.分别将x-y,a+b,x+3看作一个整体,然后再利用同底数幂的乘法法则进行计算.探究新知例5:光在真空中的速度约为3×108m/s,太阳光照射到地球上大约需要 5×102s.地球距离太阳大约有多远?解:3×108×5×102 =15×1010 = 1.5×1011(m).答:地球距离太阳大约有1.5×1011m.探究新知 1.下面的计算对不对?如果不对,应当怎样改正. (1)b3·b3=2b3 (2)b3+b3=b6 (3)a·a5·a3=a8 (4)(-x)4·(-x)4=(-x)16××××b3·b3=b6b3+b3=2b3=x8a·a5·a3=a9(-x)4·(-x)4=(-x)8随堂练习2.计算a•a2结果正确的是( )A.a B.a2 C.a3 D.a4C3. x3·x2的运算结果是( )A. x2 B. x3 C. x5 D. x6C随堂练习4.数学讲究记忆方法.如计算(a5)2时若忘记了法则,可以借助(a5)2=a5×a5=a5+5=a10,得到正确答案.你计算(a2)5﹣a3×a7的结果是_______.05.计算2x4•x3的结果等于 .2x7随堂练习6.计算:① 103×104; ② a·a3;③ a·a3·a5; ④ x·x2+x2·x.⑤ 3y2·y4-3y·y3·y2 ⑥x2·x3·x4·x=107=a4=a9=2x3=0=x10随堂练习7.计算:(1) x n · xn+1 ;(2) (x+y)3 · (x+y)4 .解:x n · xn+1 =xn+(n+1)= x2n+1am · an = am+n 公式中的a可代表一个数、字母、式子等.解:(x+y)3 · (x+y)4 =(x+y)3+4 =(x+y)7随堂练习 (4) xn+1·x2n(5)(6) (1)(-9)2×93(2)(a-b)2·(a-b)3(3)-a4·(-a)28.计算下列各题:a·a2+a3=92×93=95=(a-b)5=-a4·a2=-a6=x3n+1=a3+a3=2a3随堂练习9.一个长方形的长是4.2×104cm,宽是2×104cm,求此长方形的面积及周长.面积=长×宽=4.2×104×2×104 =8.4×108(cm2).周长=2(长+宽)=2×(4.2×104+2×104) =1.24×105(cm).综上可得长方形的面积为8.4×108cm2,周长为1.24×105cm.解:随堂练习同底数幂的乘法法则am·an=am+n (m,n都是正整数)注意同底数幂相乘,底数不变,指数相加am·an·ap=am+n+p(m,n,p都是正整数)直接应用法则常见变形:(-a)2n=a2n, (-a)2n+1=-a2n+1底数相同时底数不相同时先变成同底数,再应用法则课堂小结课程结束
相关资料
更多









