北师大版数学七年级下册 2.3.2《平行线的性质》第2课时 课件+分层练习（含答案解析）

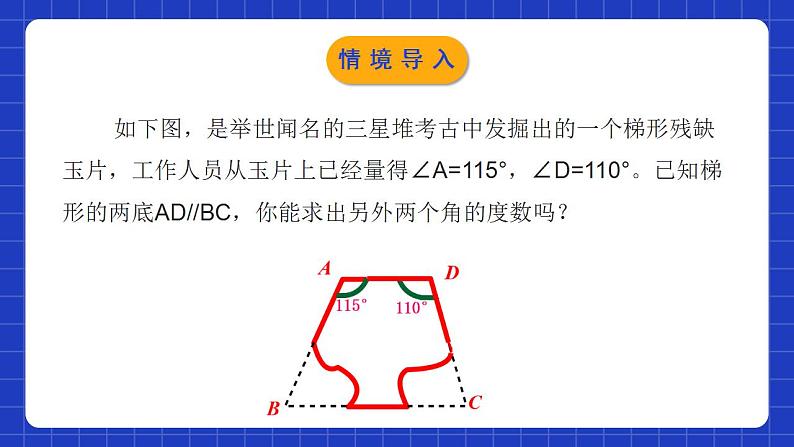
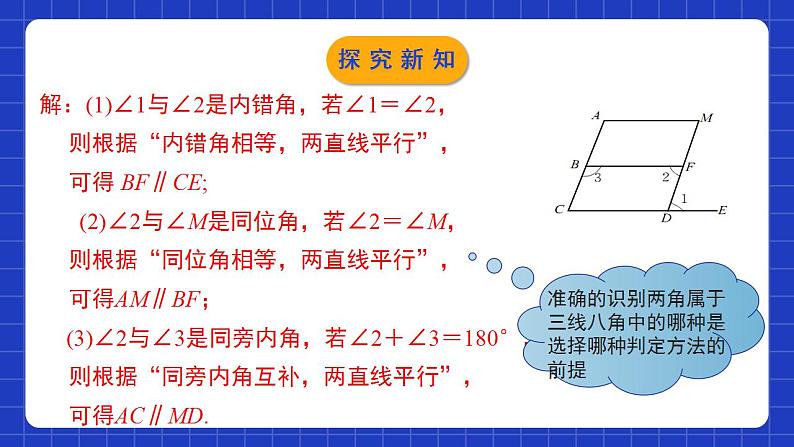
2.3.2平行线的性质第2课时学习目标1进一步掌握平行线的性质，运用两条直线是平行判断角相等或互补.2能够根据平行线的性质与判定进行简单的推理与计算.两直线平行 同位角相等内错角相等同旁内角互补平行线的判定平行线的性质直线的位置关系角的数量关系性质角的数量关系直线的位置关系判定情境导入三星堆遗址 位于中国四川省广汉市南兴镇北的三星堆遗址，属于古蜀国文明。遗址分布范围达12平方公里，距今4800年至2800年，延续时间近2000年。出土各种文物：金器、玉器、石器、陶器、青铜器...等数千件。其中有享誉中外的金杖、金面罩、青铜人像、头像、人立像、画具等精品文物1000多件。情境导入 如下图，是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片，工作人员从玉片上已经量得∠A=115°，∠D=110°。已知梯形的两底AD//BC，你能求出另外两个角的度数吗？情境导入平行线性质与判定的综合运用例1：据图回答下列问题：(1)若∠1＝∠2，则可以判定哪两条直线平行？根据是什么？(2)若∠2＝∠M，则可以判定哪两条直线平行？ 根据是什么？(3)若∠2＋∠3＝180°，则可以判定哪两条直线平行？ 根据是什么？探究新知解：(1)∠1与∠2是内错角，若∠1＝∠2， 则根据“内错角相等，两直线平行”， 可得 BF∥CE; (2)∠2与∠M是同位角，若∠2＝∠M， 则根据“同位角相等，两直线平行”， 可得AM∥BF； (3)∠2与∠3是同旁内角，若∠2＋∠3＝180°， 则根据“同旁内角互补，两直线平行”， 可得AC∥MD.探究新知例2：如图，AB∥CD，如果∠1=∠2，那么EF、AB平行吗？请说明理由. 解： 平行. 理由： ∵ ∠1=∠2 （已知） ∴ EF∥CD (内错角相等，两直线平行 ) 又∵AB∥CD（已知） ∴ EF∥AB （平行于同一条直线的两条直线平行） 探究新知例3： 如图，已知直线a∥b，直线c∥d，∠1＝107°，求∠2，∠3的度数.解：∵a∥b，∴∠2＝∠1＝107°（两直线平行，内错角相等）.∵c∥d，∴∠1＋∠3＝180°（两直线平行，同旁内角互补）,∴∠3＝180°－∠1＝180°－107°＝73°. 探究新知归纳总结平行线的“性质”与“判定”有什么不同 已知角之间的关系(相等或互补)，得到两直线平行的结论是平行线的判定。 已知两直线平行，得到角之间的关系(相等或互补)的结论是平行线的性质。探究新知 如下图，是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片，工作人员从玉片上已经量得∠A=115°，∠D=110°。已知梯形的两底AD//BC，你能求出另外两个角的度数吗？你会解决了吗？解: ∵AD//BC ,∠A=115° ∴∠A+∠B=180 °(两直线平行，同旁内角互补) ∴∠B=65° ∠C=70°探究新知 做一做：如图，若AB//CD，你能确定∠B、∠D与∠BED 的大小关系吗？说说你的看法． 解：过点E作EF//AB．所以∠B=∠BEF．因为AB//CD, 所以∠D =∠DEF．所以∠B＋∠D＝∠BEF＋∠DEF＝∠DEB．即∠B＋∠D＝∠DEB． F所以EF//CD．探究新知如图，AB//CD，探索∠B,∠D与∠DEB的大小关系.解：过点E作EF//AB． 所以∠B+∠BEF＝180°． 因为AB//CD, 所以EF//CD． 所以∠D +∠DEF＝180°． 所以∠B＋∠D+∠DEB ＝∠B＋∠D+∠BEF＋∠DEF ＝360°． 即∠B＋∠D＋∠DEB＝360°． F探究新知 讨论1：如图,AB∥CD,则 :当有一个拐点时： ∠A+∠E+∠C= 360°， 当有两个拐点时： ∠A+∠ E1 + ∠ E2 +∠C = 540°， 当有三个拐点时： ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°. 探究新知…若有n个拐点，你能找到规律吗？探究新知讨论2：如图,若AB∥CD, 则：当左边有两个角，右边有一个角时： ∠A+∠C= ∠E.当左边有两个角，右边有两个角时： ∠A+∠F= ∠E +∠D.当左边有三个角，右边有两个角时: ∠A+∠ F1 +∠C= ∠ E1 +∠ E2.探究新知若左边有n个角，右边有m个角,你能找到规律吗？探究新知1.如图，直线a，b被直线c，d所截，若∠1＝80°，∠2＝100°，∠3＝85°，则∠4的度数是(　　)A．80°B. 85°C. 95°D. 100°B随堂练习2.如图，若∠A＋∠ABC＝180°，则下列结论正确的是(　　)A．∠1＝∠2B. ∠2＝∠3C. ∠1＝∠3D. ∠2＝∠4D随堂练习3． 一小区大门的栏杆如图，当栏杆抬起时，BA垂直于地面AE，CD平行于地面AE，则∠ABC+∠BCD的度数为（　　）A． 180° B． 270° C． 300° D． 360°B随堂练习4. 如图4，AB∥CD，直线BC分别交AB，CD于点B，C. 若∠1=50°，则∠2的度数为(　　)A. 40° B. 50° C. 120° D. 130°D随堂练习5. 如图，直线MA∥NB，∠A＝70°，∠B＝40°，则∠P＝____________.30°随堂练习6. 如图，已知∠A＝∠1，∠C＝∠F.求证：BC∥EF.证明：∵∠A＝∠1(已知)∴AC∥DF(同位角相等，两直线平行)∴∠C＝∠BGD(两直线平行，同位角相等)又∵∠C＝∠F(已知)∴∠BGD＝∠F(等量代换)∴BC∥EF(同位角相等，两直线平行)随堂练习7. 如图，已知AD∥BC，∠1=∠2，试说明：∠3+∠4=180°. 解：因为AD∥BC（已知）,所以∠1=∠3（两直线平行，内错角相等）. 因为∠1=∠2（已知）,所以∠2=∠3（等量代换）. 所以BE∥DF（同位角相等，两直线平行）. 所以∠3+∠4=180°（两直线平行，同旁内角互补）. 随堂练习8.如图，点B在AC上，点E在DF上，AF分别与BD、CE相交于点G、H，且∠1＝∠2，∠C＝∠D，试说明∠A＝∠F.证明：∵AF与CE相交于点H∴∠2＝∠3(对顶角相等)∵∠1＝∠2(已知)∴∠1＝∠3(等量代换)∴DB∥EC(同位角相等，两直线平行)∴∠4＋∠C＝180°(两直线平行，同旁内角互补)又∠C＝∠D(已知)∴∠4＋∠D＝180°(等量代换)∴DF∥AC(同旁内角互补，两直线平行)∴∠A＝∠F(两直线平行，内错角相等)随堂练习9.林湾乡要修建一条灌溉水渠，如图，水渠从A村沿北偏东65°方向到B村，从B村沿北偏西25°方向到C村，水渠从C村沿什么方向修建，可以保持与AB的方向一致？解：由题可得∠1＝65°当EC保持与AB的方向一致，则EC∥BD可得：∠NCE＝∠CBD＝25°＋65°＝90°故∠2＝65°即从C村沿北偏东65°方向建设，可保持与AB的方向一致．随堂练习平行线性质与判定的综合运用的两种形式：1.角与角的数量关系→线与线的位置关系→角与角的数量关系；2.线与线的位置关系→角与角的数量关系→线与线的位置关系.课堂小结课程结束