资料中包含下列文件,点击文件名可预览资料内容







当前文件暂不支持在线预览,请下载使用
还剩23页未读,
继续阅读
成套系列资料,整套一键下载
北师大版数学七年级下册 第三章《变量之间的关系》单元小结 课件+单元测试(含答案解析)
展开
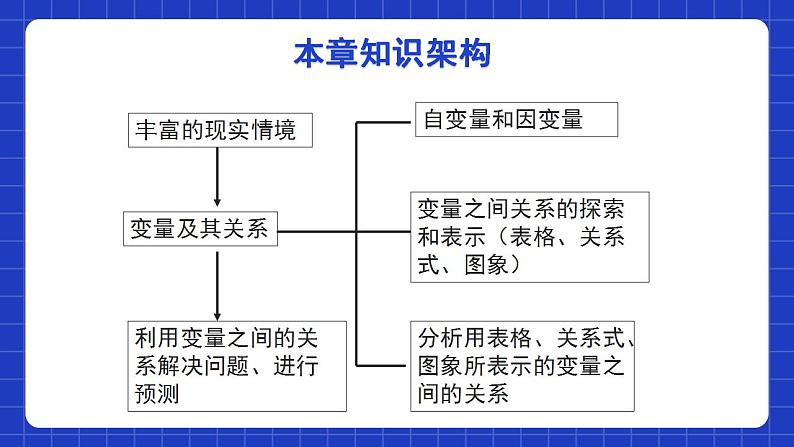
第三章 变量之间的关系单元小结丰富的现实情境变量及其关系利用变量之间的关系解决问题、进行预测自变量和因变量变量之间关系的探索和表示(表格、关系式、图象)分析用表格、关系式、图象所表示的变量之间的关系本章知识架构一、变量与函数在一个变化过程中,主动引起变化的量叫做自变量,如上课时实验中高度的变化和时间的变化被动引起变化的量叫做因变量,如上课时实验中时间的变化和人口数量的变化始终没有变化的量叫做因常量,如上课时实验中小车下滑的距离知识专题1.自变量是在一定范围内主动变化的量。2.因变量是随自变量变化而变化的量。3.表格可以表示因变量随自变量变化而变化的情况,还能帮助我们对变化趋势进行初步的预测。提示:在变化过程中起主导作用的那个变量是自变量. 知识专题 运用定义法来解答.区别自变量和因变量有以下三种方法:(1)看变化的先后顺序,自变量是先发生变化的量,因变量是后发生变化的量;(2)看变化的方式,自变量是一个主动变化的量,因变量是一个被动变化的量;(3)看因果关系,自变量是起因,因变量是结果.知识专题二、用表格表示函数:分析表格常分三步:第一步,是通过表格确定自变量与因变量第二步,是纵向观察每一列,发现因变量与自变量的对应关系第三步,是分别横向观察两栏,从中发现两变量间星现的变化趋势。求因变量的值,若不在所列数值之中,则家根据两变量之间的变化趋势进行估计。知识专题用表格表示变量之间关系的“三个一”一个优点:根据表格中已列出的自变量的值,可以直接查到与其对应的因变量的值,使用起来比较方便.一个不足:表格中所列出的对应值一般都是有限的,由表格不容易看出两个变量之间的对应规律,不能直观、形象地反映变量之间的变化趋势.一个注意:用表格表示变量之间关系时,要先表示自变量,再表示因变量,在表示自变量和因变量时,第一列要写单位名称.知识专题三、用关系式表示函数:1.关系式是我们表示变量之间关系的另一种方法,如y=3x,我们可以根据任何一个自变量值求出相应的因变量的值.关系式法:1.关系式是两个变量之间关系的定量表达;2.关系式是在给定自变量值后能确定相应的因变量的值,但是因变量可能不唯一,如y=x2知识专题2.用来表示自变量和因变量之间关系的等式叫做关系式。要点精析:关系式的基本特征是:①等式的左边是因变量,等式的右边是关于自变量的代数式;②等式中只含有自变量和因变量这两个变量,其他的量都是常量;③自变量可在允许的范围内任意取值.知识专题3.求两个变量之间的关系式常用的方法:(1)利用公式:如图形的周长公式、面积公式、体积公式等;(2)利用生活中特定的数量 关系,如行程问题中“路程=时间×速度”,销售问题中“销售额=单价×数量”等;(3)根据表格与图象中的信息列关系式(这种方法以后会学习)等.知识专题优点:简单明了,能准确反映整个变化过程中自变量与因变量的相互关系.缺点:求对应值时有时要经过比较复杂的计算,而且实际问题中,有的变量之间的关系不一定能用关系式表示出来.4.用关系式表示变量之间的关系的优缺点:知识专题四、用图像表示函数:图象是我们表示变量之间关系的又一种方法。1.用图像表示变量间的关系最大的特点就是直观;2.图像的水平数轴(横轴)上的点表示自变量,竖直数轴(纵轴)上的点表示因变量;3.图像能较为直观的反映变化趋势知识专题 图象(或其局部)如果呈“/”(含“ ”“ ”等)状,就说明因变量随着自变量的增加而增加.图象(或其局部)如果呈“\”(含“ ”“ ”等)状,就表示因变量随着自变量的增加而减少.图象呈“ ”(含“∧”等)状,表示因变量先随着自变量的增加而增加,然后随着自变量的增加而减少.图象呈“ ”(含“∨”等)状,表示因变量先随着自变量的增加而减少,然后随着自变量的增加而增加.知识专题(1)注意两数轴上的名称与单位图象的识图技巧(3)识图关键:弄清图象上点的意义,找准关键点:注意图象的起点、终点、最高点、最低点、拐点等特殊位置,并弄清这些点所表示的意义.(2)分布规律:横轴上的点表示自变量,纵轴上的点表示因变量.知识专题加速速度v时间t速度v时间t减速速度v时间t匀速速度v时间t停止速度v时间t减速加速00000变化速率相同变化速率不同速度v时间t0探究速度随时间的变化知识专题 怎样通过图象判断速度随时间变化的情况?增大减小保持不变1.怎样看图:静止不动从左往右随着时间的变化:若图象上升,表明速度在 ;若图象下降,表明速度在 ;若图象与横轴平行,则表明速度 .若图象在横轴上,表明 .2.倾斜程度:陡——变化速率快 缓——变化速率慢 知识专题路程s时间t路程s时间t路程s时间t匀速路程s时间t停止路程s时间t变速加速路程s时间t变速减速匀速停止渐行渐远回到原地000000回到原地渐行渐远探究路程随时间的变化知识专题怎样通过图象判断路程随时间变化的情况2.倾斜程度:陡——速度越快 缓——速度越慢 1.随着时间的增加若图象上升,表明路程在 ; 若图象下降,表明离原地的路程 ; 若图象与横轴平行,则表明路程 . 增加减少保持不变知识专题三种表示变量之间关系的方法和优缺点:知识专题例1 : 一名同学在用弹簧做实验,在弹簧上挂不同质量的物体后,弹簧的长度也 不同,实验数据如下表:(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?解:反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量,弹簧的长度是因变量.考点专练例1 : 一名同学在用弹簧做实验,在弹簧上挂不同质量的物体后,弹簧的长度也 不同,实验数据如下表:解:弹簧不挂物体时的长度是12 cm,随着 x 的变化,y 的变化趋势是 y=12+0.5x.(2)弹簧不挂物体时的长度是多少?如果用 x 表示弹性限度内物体的质量,用 y 表示弹簧的长度,那么随着 x 的变化,y 的变化趋势如何?考点专练例1 : 一名同学在用弹簧做实验,在弹簧上挂不同质量的物体后,弹簧的长度也 不同,实验数据如下表:(3)如果弹簧最大挂重为 15 kg,你能预测当挂重为 10 kg时,弹簧的长度是多少?解:当 x=10 时,y=12+0.5x=17,即此时弹簧的长度是17 cm.考点专练例2:如图,将边长为20 cm的正方形纸片的四个角截去相同的小正方形,然后将截好的材料围成一个无盖的长方体.考点专练(1)这个情境反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量? 反映了截取的小正方形的边长与围成的无盖长方体的体积之间的关系,其中小正方形的边长是自变量,长方体的体积是因变量.(2)在以上问题中,若设截去的小正方形的边长是 x cm,围成的无盖长方体的体积是 y cm3,则 y 与 x 之间的关系式是__________________. y =x(20-2x)2考点专练(3)若小正方形的边长是5 cm,则长方体的体积是多少立方厘米?那当 x = 2.5 cm呢?当 x=5 时,y =x(20-2x)2 =500,即此时长方体的体积是 500 cm3.当 x=2.5 时,y =x(20-2x)2 =562.5,即此时长方体的体积是 562.5 cm3.(4)根据以上关系式填下表.32451258857650038425212836考点专练(5)当 x 在什么范围变化时,y 随 x 的增大而增大,当 x 在什么范围变化时, y 随 x 的增大而减小?你又是根据哪种表示法得到的?当 x<3时,y 随 x 的增大而增大,当 x >3 时, y 随 x 的增大而减小,是根据列表法得到的.考点专练例3:小红与小兰从学校出发到距学校 5 千米的书店买书,图象反映了她们两人离开学校的路程与时间的关系.根据图象解决问题.考点专练(1)小红与小兰谁先出发?谁先达到?小兰先出发,小兰和小红同时到达.(2)小兰前20分的速度和最后10分的速度是多少?小兰前20分的速度为6千米/时,最后10分的速度为18千米/时.(3)小红与小兰从学校到书店的平均速度各是多少?小红的平均速度为6千米/时,小兰的平均速度为5千米/时.考点专练例4:一辆汽车以每时 50 千米的速度行驶了 t 时,行驶路程为 s 千米. (1)这个情境中,有哪些变量?其中自变量是什么?因变量是什么? (2)你能用哪种方式表示路程与时间之间的关系? 行驶路程和行驶时间是变量,其中行驶时间是自变量,行驶路程是因变量.路程与时间的关系为 s = 50t.考点专练例4:一辆汽车以每时 50 千米的速度行驶了 t 时,行驶路程为 s 千米. (3)该汽车行驶 2.5 时的路程是多少千米?(4)一段公路全长 350 千米,这辆汽车行驶完全程需要多少时?125千米7时考点专练课程结束
相关资料
更多









