资料中包含下列文件,点击文件名可预览资料内容






当前文件暂不支持在线预览,请下载使用
还剩13页未读,
继续阅读
成套系列资料,整套一键下载
北师大版数学七年级下册 第五章《生活中的轴对称》单元小结 课件+单元测试(含答案解析)
展开
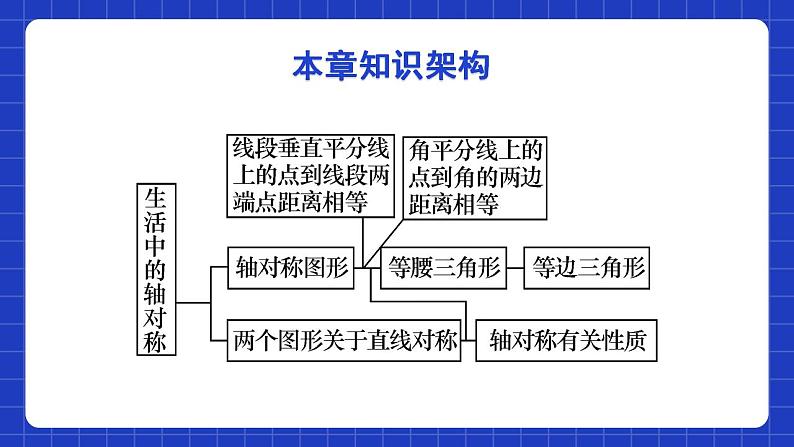
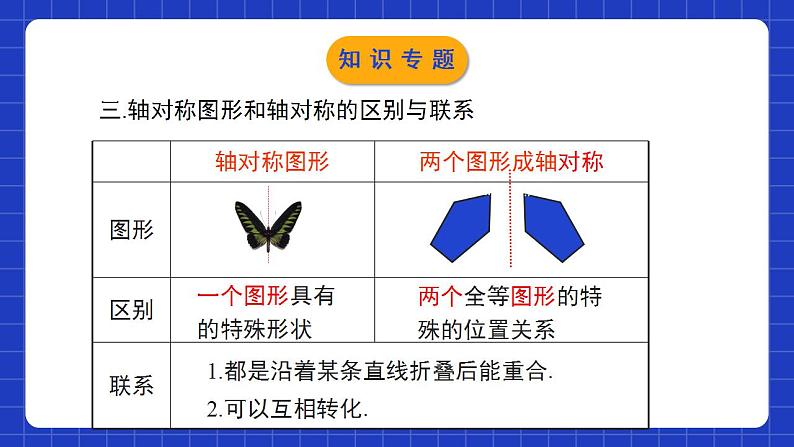
第五章 生活中的轴对称单元小结本章知识架构知识专题一、轴对称图形 如果 沿一条直线折叠,直线两旁的部分能够 ,那么这个图形叫作 .这条直线就是它的 .一个平面图形互相重合轴对称图形对称轴二、轴对称对称轴1.定义: 如果两个平面图形沿一条直线对折后能够完全重合,那么称这两个图形成轴对称,这条直线叫作这两个图形的对称轴.2.轴对称的定义包含两层含义:(1)有两个图形,且形状、大小完全相同.(2)两个图形的位置必须满足沿一条直线对折后能完全重合.知识专题三.轴对称图形和轴对称的区别与联系 一个图形具有的特殊形状两个全等图形的特殊的位置关系1.都是沿着某条直线折叠后能重合.2.可以互相转化.知识专题四、轴对称的性质: 1.轴对称的基本性质: 在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.2.性质的应用:利用对应角相等求角度;利用对应线段相等求线段,求面积,求周长;作图.知识专题五、等腰三角形的性质1.等腰三角形是轴对称图形.2.等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”).3.等腰三角形的两个底角相等.知识专题六、等边三角形的性质1.等边三角形是轴对称图形,共有三条对称轴。2.等边三角形每个角的平分线和这个角的对边上的中线、高线重合(简称“三线合一”),它们所在的直线都是等边三角形的对称轴。3.等边三角形的各角都相等,都等于60°知识专题七、线段的垂直平分线1.垂直于一条线段,并且平分这条线段的直线,叫作 这条线段的垂直平分线. 2.线段垂直平分线的性质: 线段垂直平分线上的点到这条线段两个端点的距离相等.3 线段的对称轴是这条线段的垂直平分线.知识专题八、角平分线的性质角的平分线上的点到角的两边的距离相等.2.应用所具备的条件:3.定理的作用: 证明线段相等.1.角平分线的性质:知识专题例1:下列图形对称轴最多的是( )A. 正方形 B. 等边三角形 C. 等腰三角形 D.线段正解:A. 有4条对称轴,即两条对角线所在的直线和两组对边的垂直平分线;B. 有3条对称轴,即各边的垂直平分线;C. 有1条对称轴,即底边的垂直平分线;D. 有2条对称轴.答案:A考点专练易错提示:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做轴对称图形的对称轴.解答本题的过程中,根据定义将每一条对称轴找出.考点专练例2:如图,△AOD关于直线l进行轴对称变换后得到△BOC,下列说法不正确的是( )A. ∠DAO=∠CBO,∠ADO=∠BCOB. 直线l垂直平分AB、CDC. AO⊥OB, DO⊥OCD. AD=BC,OD=OC考点专练正解:因为△AOD关于直线l进行轴对称变换后得到△BOC,所以∠DAO=∠CBO,∠ADO=∠BCO,直线l垂直平分AB,CD,AD=BC,OD=OC.因为题设中没有给定△AOD为等腰三角形,所以△BOC的形状不能确定.所以A,B,D选项的说法正确;C选项的说法错误.答案:C考点专练易错提示:根据轴对称的性质易得∠DAO=∠CBO,∠ADO=∠BCO,直线l垂直平分AB,CD,AD=BC,OD=OC.选项C中对应线段OA与OB,OD与OC分别关于对称轴重合,但不一定垂直,所以该选项有误.考点专练例3:如果等腰三角形两边长是3 cm和6 cm,那么它的周长是( )A.9 cm B.12 cmC.15 cm D.12 cm或15 cm正解:当腰长为6 cm时,则三角形的三边长分别为6 cm,6 cm,3 cm,满足三角形的三边关系,此时周长为15 cm;当腰长为3 cm时,则三角形的三边长分别为3 cm,3 cm,6 cm,此时3+3=6,不满足三角形的三边关系,不符合题意.答案:C考点专练易错提示:解答本题时因为题中没有指明腰的长度和底边的长度,所以要对已知的边长3 cm和6 cm 进行分类讨论.考点专练例4:下列各图中,OP 是∠MON 的平分线,点E,F,G 分别在射线OM,ON,OP 上,则可以解释“角的平分线上的点到角两边的距离相等”的图形是( )考点专练正解:因为OP是∠MON 的平分线,且GE⊥OM,GF⊥ON,所以GE=GF(角的平分线上的点到角两边的距离相等).答案:D考点专练易错提示:角的平分线上的点到角两边的距离相等,这里的距离是指点到角的两边垂线段的长而不是任意点的连线段,本题中只有选项D是满足题意的,A,B,C中都不符合角平分线的定义.考点专练课程结束
相关资料
更多









