资料中包含下列文件,点击文件名可预览资料内容




当前文件暂不支持在线预览,请下载使用
还剩17页未读,
继续阅读
成套系列资料,整套一键下载
北师大版数学七年级下册 6.2.2《频率的稳定性》第2课时 课件+分层练习(含答案解析)
展开
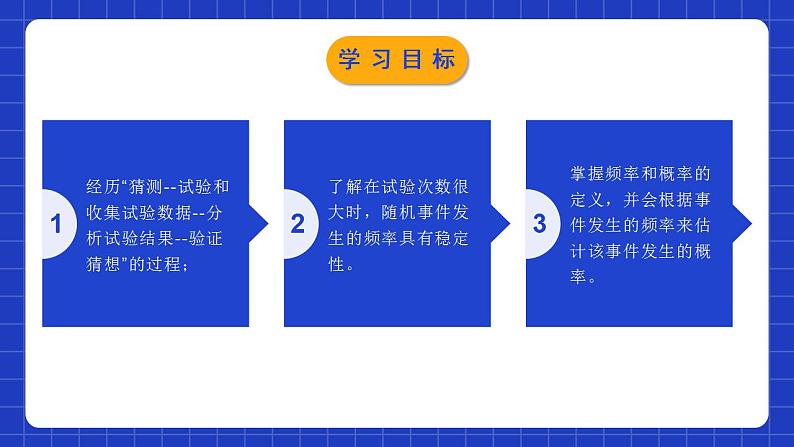
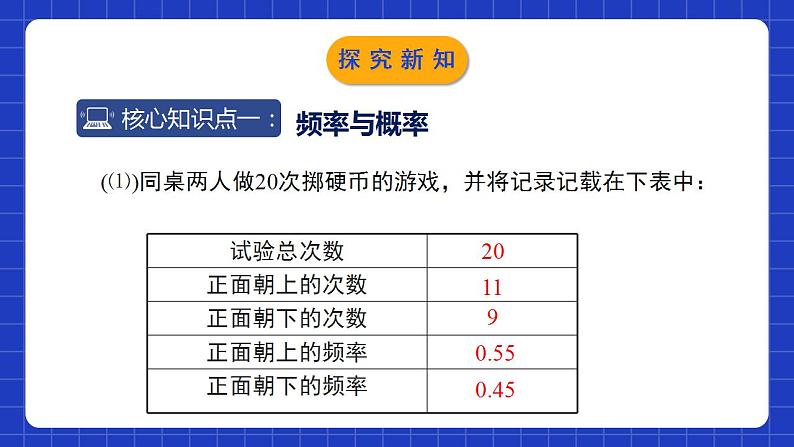
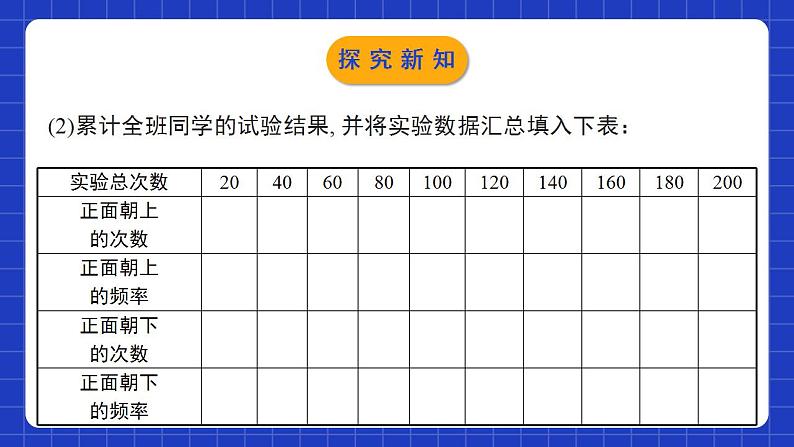
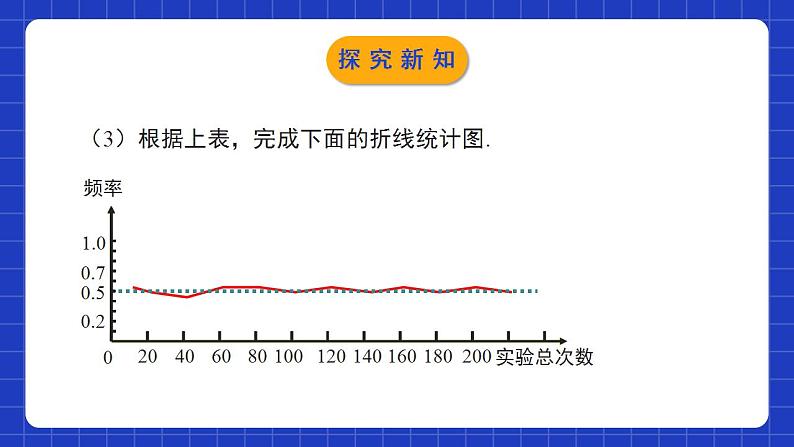
6.2.2频率的稳定性第2课时学习目标1经历“猜测--试验和收集试验数据--分析试验结果--验证猜想”的过程;2了解在试验次数很大时,随机事件发生的频率具有稳定性。 3掌握频率和概率的定义,并会根据事件发生的频率来估计该事件发生的概率。1.有些事件我们事先肯定它一定会发生,这些事件称为必然事件。2.有些事件我们事先肯定它一定不会发生,这些事件称为不可能事件。3.必然事件和不可能事件都是确定事件。4.有些事件我们事先无法肯定它会不会发生,这样的事件称为不确定事件,也称为随机事件。★一般地,不确定事件发生的可能性是有大小的。情境导入足球比赛开场是用什么方式决定哪个队先开球的?抛掷一枚均匀的硬币,硬币落下后,会出现什么情况:正面朝上正面朝下你觉得公平吗?情境导入频率与概率同桌两人做20次掷硬币的游戏,并将记录记载在下表中:20110.4590.55探究新知 (2)累计全班同学的试验结果, 并将实验数据汇总填入下表:探究新知实验总次数(3)根据上表,完成下面的折线统计图.探究新知(4)观察上面的折线统计图,你发现了什么规律? 随着实验的次数的增加,折线在“0.5水平直线”的上下摆动的幅度会逐渐变小.当抛掷硬币的次数很大时,正面朝上的频率都会在一个常数0.5附近摆动,即硬币正面朝上的频率具有稳定性.探究新知下表列出了一些历史上的数学家所做的掷硬币实验的数据:表中的数据支持你发现的规律吗?探究新知归纳总结 无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性. 由于事件A发生的频率,表示该事件发生的频繁程度,频率越大,事件A发生越频繁,这就意味着事件A发生的可能性也越大,因而,我们就用这个常数来表示事件A发生的可能性的大小.我们把刻画事件A发生的可能性大小的数值,称为事件A发生的概率,记为P (A).探究新知归纳总结概率的意义:事件发生的可能性的大小概率的数值:为频率的稳定值(概率与频率的关系)探究新知归纳总结 事件A发生的概率P(A)的取值范围是什么?必然事件、不可能事件以及随机事件发生的概率分别是多少?必然事件发生的概率为1;不可能事件发生的概率为0;随机事件A发生的概率P(A)是0与1之间的一个常数探究新知例:瓷砖生产受烧制时间、温度、材质的影响,一块砖坯放在炉中烧制,可能成为合格品,也可能成为次品或废品,究竟发生那种结果,在烧制前无法预知,所以这是一种随机现象.而烧制的结果是“合格品”是一个随机事件,这个事件的概率称为“合格品率”. 由于烧制结果不是等可能的,我们常用“合格品”的频率作为“合格品率”的估计.探究新知 某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,结果如下:(1)计算上表中合格品率的各频率(精确到0.001);(2)估计这种瓷砖的合格品率(精确到0.01);(3)若该厂本月生产该型号瓷砖500000块,试估计合格品数.探究新知解:(1)逐项计算,填表如下:(3)500000×96%=480000(块),可以估计该型号合格品数为480000块.探究新知1.已知抛一枚均匀硬币正面朝上的概率为 ,下列说法错误的是( )A.连续抛一枚均匀硬币2次必有1次正面朝上B.连续抛一枚均匀硬币10次都可能正面朝上C.大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次D.通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的A随堂练习2.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )A.频率就是概率B.频率与试验次数无关C.概率是随机的,与频率无关D.随着试验次数的增加,频率一般会越来越接近概率D随堂练习3.某射击运动员在同一条件下的射击成绩记录如下:根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )A.0.90 B.0.82 C.0.85 D.0.84B随堂练习4.下列事件发生的可能性为0的是( )A.掷两枚骰子,同时出现数字“6”朝上B.小明从家里到学校用了10分钟, 从学校回到家里却用了15分钟 C.今天是星期天,昨天必定是星期六D.小明步行的速度是每小时40千米D随堂练习5.口袋中有9个球,其中4个红球, 3个蓝球,2个白球,在下列事件中,发生的可能性为1的是( ) A.从口袋中拿一个球恰为红球 B.从口袋中拿出2个球都是白球 C.拿出6个球中至少有一个球是红球 D.从口袋中拿出的球恰为3红2白C随堂练习6.(1)把标有号码1、2、3……,10的10个乒乓球放在一个箱子中,摇匀后,从中任意取一个,号码为小于7的奇数的概率是____.(2)在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒子中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后发现,摸到红球的频率稳定在0.2,那么可以推算出n大约是 .10随堂练习7.某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:随堂练习(1)这种树苗成活的频率稳定在____,成活的概率估计值为____.(2)该地区已经移植这种树苗5万棵.①估计这种树苗成活____万棵;②如果该地区计划成活18万棵这种树苗,那么还需要移植这种树苗约多少万棵?解:(2)设还需要移植x万棵,则(x+5)×0.9=18,解得x=15.答:还需要移植这种树苗约15万棵.0.90.94.5随堂练习4.必然事件发生的概率为1;不可能事件发生的概率为0;随机事件A发生的概率P(A)是0与1之间的一个常数.3.一般的,大量重复的实验中,我们常用随机事件A发生的频率来估计事件A发生的概率.2.事件A的概率,记为P(A).1.频率的稳定性.课堂小结课程结束
相关资料
更多









