1.1.2《空间向量的数量积 》课件+教案+分层练习+导学案（含答案解析）-人教版高中数学选修一

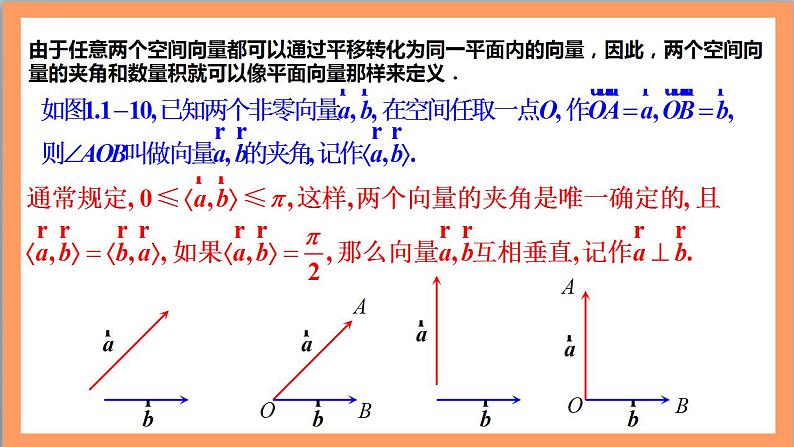
1.1.2《空间向量的数量积运算》人教版高中数学选修一掌握空间向量的夹角的概念，培养数学抽象的核心素养．掌握空间向量的数量积的定义、性质、运算律，提升数学抽象的核心素养．了解空间向量投影的概念以及投影向量的意义，培养直观想象的核心素养．能用空间向量的数量积解决立体几何中的垂直、夹角、长度等问题，强化数学运算的核心素养. 学习目标 根据功的计算，我们定义了平面向量的数量积运算，一旦定义出来，我们发现这种运算非常有用，它能解决有关长度和角度问题，在空间向量中亦是如此。． 在必修第二册中我们还学习了平面向量的数量积运算，现在我们类比平面向量数量积的运算，学习空间向量的数量积运算.新课引入问题1:类比平面向量的数量积，你能得出空间向量的数量积 相关知识？ 请同学们类比平面向量的数量积运算研究空间向量数量积运算，小组合作完成表格.新知探究OBAOBA由于任意两个空间向量都可以通过平移转化为同一平面内的向量，因此，两个空间向量的夹角和数量积就可以像平面向量那样来定义．特别地，零向量与任意向量的数量积为0．7问题2：根据平面向量数量积的学习经验，为了研究数量积的运算律，需要先定义向量的投影.想一想空间向量的投影有哪些情况.问题3：下面我们分情况展开空间向量投影的研究.如图1(1),如何定义并画出空间向量 向向量 投影？(1)AB(1)(2)(3)图1.1-11AB(1)(2)(3)图1.1-11 由于空间向量的线性运算和数量积运算具有鲜明的几何背景，空间图形的许多性质可以由向量的线性运算及数量积运算表示出来，因此，立体几何中的许多问题可以用向量运算的方法加以解决．图1.1-13lmng1. 空间向量的夹角(1) 两向量的夹角是唯一确定的(2) 夹角范围(3) 特殊夹角及对应两向量的位置关系2. 空间向量的数量积的定义与几何意义3. 空间向量数量积的性质：证明向量垂直的方法；计算向量长度的方法。4. 空间向量数量积的运算律。课堂总结问题7.请同学们回顾本节课的学习内容,并回答下列问题：1. 本节课学习的概念有哪些？2. 在解决问题时，用到了哪些数学思想？作业布置：教科书1.习题1.12.第4,7题.作业布置ABCC1A1B1(第1题)练习（第8页）B课堂检测BDA(第2题)CABCD(第3题)ABDCabc(第4题)ABCDEF习题1.1（第9页）ABCD(第2题)E(第2题)ABCDEFG(第4题)ABCDEFG(第4题)ABCDD1C1B1A1M(第5题)AABCDEFGH(第6题)6．如图，已知E，F，G，H分别为四面体ABCD的棱AB，BC，CD，DA的中点，求证： E，F，G，H四点共面．ABCDABCDABOCD8．用向量方法证明：在平面内的一条直线，如果与这个平面的一条斜线在这个平面上的射影垂直，那么它也与这条斜线垂直（三垂线定理）．ABCOABCHFEOGABCHFEOG课程结束人教版高中数学选修一