资料中包含下列文件,点击文件名可预览资料内容






















还剩19页未读,
继续阅读
成套系列资料,整套一键下载
- 1.1.2《空间向量的数量积 》课件+教案+分层练习+导学案(含答案解析)-人教版高中数学选修一 课件 9 次下载
- 1.2《空间向量基本定理》课件+教案+分层练习+导学案(含答案解析)-人教版高中数学选修一 课件 10 次下载
- 1.3.2《空间向量运算的坐标表示》课件+教案+分层练习+导学案(含答案解析)-人教版高中数学选修一 课件 9 次下载
- 1.4.1 用空间向量研究直线、平的位置关系(第1课时)课件+教案+分层练习+导学案(含答案解析)-人教版高中数学选修一 课件 9 次下载
- 1.4.1 用空间向量研究直线、平的位置关系(第2课时)课件+教案+分层练习+导学案(含答案解析)-人教版高中数学选修一 课件 8 次下载
1.3.1《空间直角坐标系》课件+教案+分层练习+导学案(含答案解析)-人教版高中数学选修一
展开
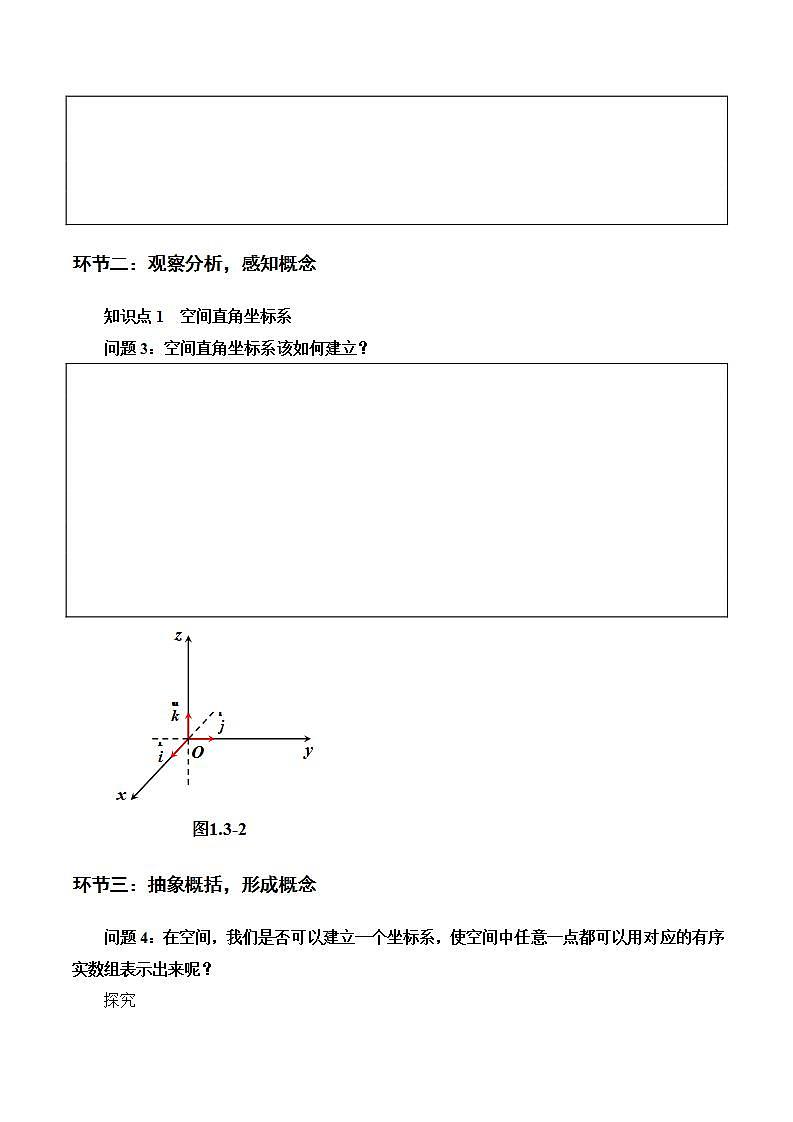
1.3.1《空间直角坐标系》人教版高中数学选修一 学习了空间向量基本定理,建立了“空间基底”的概念,我们就可以利用基底表示任意一个空间向量,进而把空间向量的运算转化为基向量的运算. 所以,基底概念的引入为几何问题代数化奠定了基础.了解空间直角坐标系的有关概念理解空间向量的坐标表示,培养直观想象的核心素养;会根据坐标找相应的点和向量,学写一些简单几何体的有关坐标,发展数学运算和逻辑推理等素养;掌握空间向量及其运算的坐标表示,提升数学运算的核心素养.学习目标 引导语:“为了把空间向量的运算转化为数的运算,能否利用空间向量基本定理和空间的单位正交基底,建立空间直角坐标系,进而建立空间向量的坐标与空间点的坐标的一一对应呢?”课堂引入问题1:在初中,我们学过数轴,那么什么是数轴?决定数轴的因数有哪些?数轴上的点怎么表示?新知探究问题2:在初中,我们学过直角坐标系,那么如何建立平面直角坐标系的因素有哪些?决定平面直角坐标系有哪些?平面直角坐标系中的点怎样表示?问题3:空间直角坐标系该如何建立?Oxy图1.3-2z在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,如果中指指向z轴的正方向,则称这个坐标系为右手直角坐标系.本书建立的坐标系都是右手直角坐标系.问题4:在空间,我们是否可以建立一个坐标系,使空间中任意一点都可以用对应的有序实数组表示出来呢?探究在平面直角坐标系中,每一个点和向量都可用一对有序实数(即它的坐标)表示.对空间直角坐标系中的每一个点和向量,是否也有类似的表示呢?Oxyz图1.3-3AOxyz图1.3-4这样,在空间直角坐标系中,空间中的点和向量都可以用三个有序实数表示.问题5:建立空间直角坐标系后,空间中任意一点A如何用坐标表示呢?OxyzABCD图1.3-5OABCxyz图1.3-6课堂练习OABCxyz图1.3-6OABCxyz图1.3-6OABCxyz图1.3-61. 空间直角坐标系是如何建立的?2. 空间直角坐标系,中点的坐标是如何确定的?3. 空间直角坐标系中点的位置的确定方法是什么?课堂归纳练习(第18页)目标检测OABCxyzPOABCxyzP课程结束人教版高中数学选修一
相关资料
更多









