湖北省荆州市部分县市2022-2023学年八年级上学期9月质量评价数学试题

这是一份湖北省荆州市部分县市2022-2023学年八年级上学期9月质量评价数学试题，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共10小题，每小题只有唯一正确答案，每小题3分，共30分）
1．下列各组图形中，BD是△ABC的高的图形是（ ）
A． B． C． D．
第3题图
2．设三角形三边之长分别为6，a，2，则a的值可能为（ ）
A．6B．4
C．8D．3
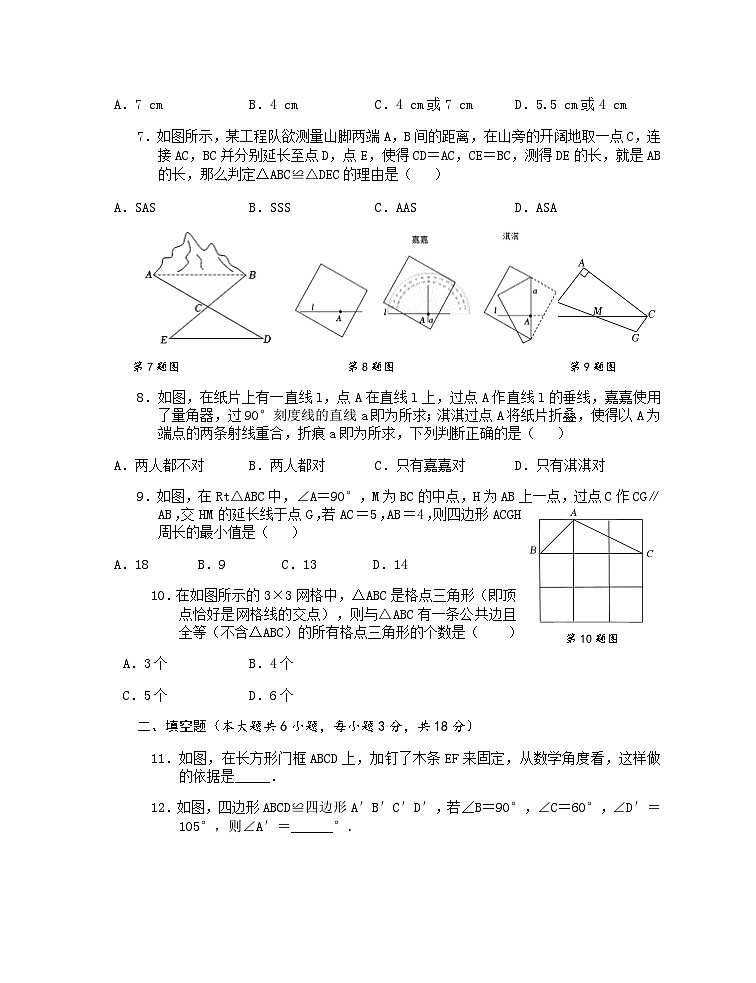
3．如图，点B，E，C，F在同一直线上，△ABC≌△DEF，BC＝8，BF＝13，则BE的长为（ ）
A．4B．5
第4题图
C．6.5D．8
4．如图是一副三角尺拼成的图案，则∠AEB的度数为（ ）
A．105°B．90°
C．75°D．60°
5．下列说法中正确的是（ ）
A.三角形的外角大于任何一个内角
B.三角形的一个外角等于两个内角的和
C.三角形的外角和小于四边形的外角和
D.三角形的内角和小于外角和
6．等腰三角形的周长为15 cm，其中一边长为4 cm，则该等腰三角形的底边长为（ ）
A．7 cm B．4 cm C．4 cm或7 cmD．5.5 cm或4 cm
7．如图所示，某工程队欲测量山脚两端A，B间的距离，在山旁的开阔地取一点C，连接AC，BC并分别延长至点D，点E，使得CD＝AC，CE＝BC，测得DE的长，就是AB的长，那么判定△ABC≌△DEC的理由是（ ）
A．SASB．SSSC．AASD．ASA

第7题图 第8题图第9题图
8．如图，在纸片上有一直线l，点A在直线l上，过点A作直线l的垂线，嘉嘉使用了量角器，过90°刻度线的直线a即为所求；淇淇过点A将纸片折叠，使得以A为端点的两条射线重合，折痕a即为所求，下列判断正确的是（ ）
A．两人都不对B．两人都对C．只有嘉嘉对D．只有淇淇对
第10题图
9．如图，在Rt△ABC中，∠A＝90°，M为BC的中点，H为AB上一点，过点C作CG∥AB，交HM的延长线于点G，若AC＝5，AB＝4，则四边形ACGH周长的最小值是（ ）
A．18 B．9 C．13 D．14
10．在如图所示的3×3网格中，△ABC是格点三角形（即顶点恰好是网格线的交点），则与△ABC有一条公共边且全等（不含△ABC）的所有格点三角形的个数是（ ）
A．3个B．4个
C．5个D．6个
二、填空题（本大题共6小题，每小题3分，共18分）
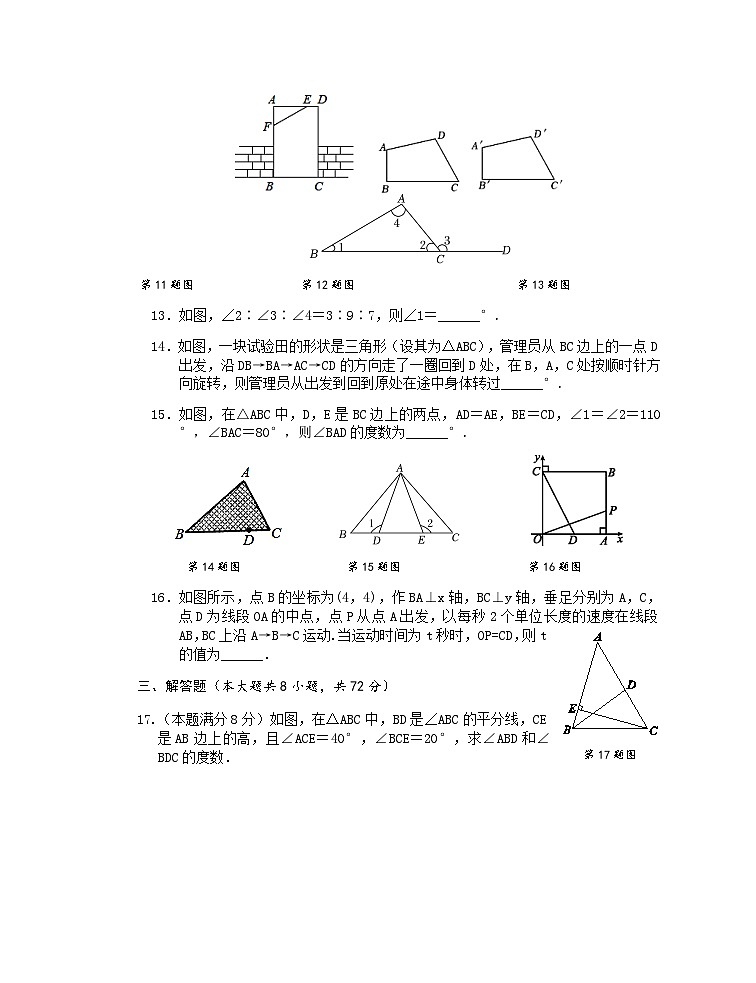
11．如图，在长方形门框ABCD上，加钉了木条EF来固定，从数学角度看，这样做的依据是_____．
12．如图，四边形ABCD≌四边形A′B′C′D′，若∠B＝90°，∠C＝60°，∠D′＝105°，则∠A′＝______°．

第11题图第12题图第13题图
13．如图，∠2∶∠3∶∠4＝3∶9∶7，则∠1＝______°．
14．如图，一块试验田的形状是三角形（设其为△ABC），管理员从BC边上的一点D出发，沿DB→BA→AC→CD的方向走了一圈回到D处，在B，A，C处按顺时针方向旋转，则管理员从出发到回到原处在途中身体转过______°．
15．如图，在△ABC中，D，E是BC边上的两点，AD＝AE，BE＝CD，∠1＝∠2＝110°，∠BAC＝80°，则∠BAD的度数为______°．

第14题图第15题图第16题图
第17题图
16．如图所示，点B的坐标为(4，4)，作BA⊥x轴，BC⊥y轴，垂足分别为A，C，点D为线段OA的中点，点P从点A出发，以每秒2个单位长度的速度在线段AB，BC上沿A→B→C运动.当运动时间为t秒时，OP=CD，则t的值为______．
三、解答题（本大题共8小题，共72分）
17.（本题满分8分）如图，在△ABC中，BD是∠ABC的平分线，CE是AB边上的高，且∠ACE＝40°，∠BCE＝20°，求∠ABD和∠BDC的度数．
第18题图
18.（本题满分8分）如图所示，已知AD，AE分别是△ABC的高和中线，AB＝10cm，AC＝24cm，BC＝26cm，∠CAB＝90°．
（1）求△ACE与△ABE的周长的差；
（2）求AD的长．
19.（本题满分8分）沿着图中的虚线，用两种方法将下面的图形划分为两个全等的图形．

第19题图
第20题图
20.（本题满分8分）如图为某单摆装置示意图，摆线长OA＝OB＝OC＝30cm，当摆线位于OB位置时，过点B作BD⊥OA于点D，当摆线位于OC位置时，OB与OC恰好垂直，过点C作CE⊥OA于点E，测得CE＝24cm．
（1）试说明OE=BD；
（2）求AD的长．
第21题图
21.（本题满分8分）如图，已知EB∥CF，OA＝OD，AE＝DF．求证：
（1）OB=OC；
（2）AB∥CD．
第22题图
22.（本题满分10分）如图1，点M，N分别在正五边形ABCDE的边BC，CD上，BM=CN，连结AM，BN相交于H．
（1）求正五边形ABCDE外角的度数；
（2）求∠AHB的度数；
（3）如图2，将条件中的“正五边形ABCDE”换成“正六边形ABCDEF”，其他条件不变，试猜想∠AHB的度数．
23.（本题满分10分）【概念认识】如图①，在∠ABC中，若∠ABD＝∠DBE＝∠EBC，则BD，BE叫做∠ABC的“三分线”．其中，BD是“邻AB三分线”，BE是“邻BC三分线”．
【问题解决】
（1）如图②，在△ABC中，∠A＝70°，∠B＝44°，若∠C的三分线CD交AB于点D，求∠BDC的度数；
（2）如图③，在△ABC中，BP，CP分别是∠ABC邻BC三分线和∠ACB邻BC三分线，若∠A＝63°，求∠BPC的度数．
第23题图
第24题图
24.（本题满分12分）如图1，在平面直角坐标系中，点A(a，0)，B(0，b)，a，b满足．
（1）直接写出A，B两点的坐标，A________，B________；
（2）如图1，过点B作BC⊥AB，且BC=AB，求点C的坐标；
（3）如图2，过点A作AD⊥AB，且AD=AB，过点A作AE⊥AO，且AE=AO，连接DE交x轴于点P，求AP的长．
参考答案
一、选择题
1.C 2.A 3.B 4.C 5.D 6.C 7.A 8.B 9.D 10.B
二、填空题
11.三角形的稳定性 12.105 13.30 14.360 15.20 16.1或3（对一个得2分）
三、解答题
17.解：∵CE是AB边上的高，
∴∠BEC＝90°，
∴∠ABC＝90°－∠BCE＝70°，
∵BD是∠ABC的平分线，
∴∠ABD＝∠ABC＝35°； ………（4分）
∵∠A＝90°－∠ACE＝50°，
∴∠BDC＝∠ABD＋∠A＝35°+50°＝85°. ………（8分）
18.解：（1）∵AE为BC边上的中线，
∴BE＝CE，
∴△ACE的周长−△ABE的周长＝AC＋AE＋CE−（AB＋BE＋AE）＝AC−AB＝24−10＝14（cm），即△ACE与△ABE的周长的差是14cm； ………（4分）
（2）∵∠CAB＝90°，AD是边BC上的高，
∴S△ABC=AB•AC＝BC•AD，
∴AD＝AB•AC÷BC＝10×24÷26＝（cm），
即AD的长度为cm． ………（8分）
19.解：如图所示（任意两种方法，正确即可）： ………（每种方法4分）

20.解：（1）∵OB⊥OC，
∴∠BOD+∠COE＝90°，
∵CE⊥OA，BD⊥OA，
∴∠CEO＝∠ODB＝90°，
∴∠BOD+∠B＝90°，
∴∠COE＝∠B，
在△COE和△OBD中，
，
∴△COE≌△OBD（AAS），
∴OE＝BD； ………（5分）
（2）∵△COE≌△OBD，
∴CE＝OD＝24cm，
∵OA＝30cm，
∴AD=OA-OD=6cm． ………（8分）
21.证明：（1）∵EB∥CF，
∴∠E＝∠F，
∵OA＝OD，AE＝DF，
∴OE＝OF，
在△OBE和△OCF中，
，
∴△OBE≌△OCF（ASA）， ………（3分）
∴OB＝OC， ………（4分）
（2）在△ABO和△DCO中，
，
∴△ABO≌△DCO（SAS）， ………（6分）
∴∠3＝∠4，
∴AB∥CD． ………（8分）
22.解：（1）∵正五边形的内角和为(5﹣2)×180°＝540°，
∴∠ABC＝×540°＝108°，
∴正五边形ABCDE外角的度数为180°﹣108°＝72°； ………（3分）
（2）在△ABM和△BCN中，
，
∴△ABM≌△BCN（SAS），
∴∠BAM＝∠CBN，
∴∠BAM+∠ABH＝∠CBN+∠ABH＝∠ABC＝108°，
∴∠AHB＝180°﹣(∠BAM+∠ABH)＝72°； ………（8分）
（3）∠AHB＝60°． ………（10分）
23.解：（1）∵∠A＝70°，∠B＝44°，
∴∠ACB＝66°，
①当CD是“邻AC三分线”时，∠ACD＝∠ACB＝22°，
∠BDC＝∠ACD+∠A＝22°＋70°＝92°； ………（3分）
②当CD是“邻BC三分线”时，∠ACD＝∠ACB＝44°，
∠BDC＝∠ACD+∠A＝44°＋70°＝114°； ………（6分）
（2）∵BP，CP分别是∠ABC邻BC三分线和∠ACB邻BC三分线，
∴∠PBC＝∠ABC，∠PCB＝∠ACB，
∵∠A＝63°，
∴∠ABC+∠ACB＝180°-∠A＝117°，
∴∠PBC＋∠PCB＝(∠ABC+∠ACB)＝39°，
∴∠BPC＝180°-(∠PBC+∠PCB)＝141°. ………（10分）
24.解：（1）（-5，0），（0，2）； ………（2分）
（2）过点C作CH⊥y轴于H，则∠CHB=90°，
∴∠C+∠CBH=90°，∠CHB=∠AOB，
∵BC⊥AB，
∴∠ABO+∠CBH=90°，
∴∠C=∠ABO，
在△CBH和△BAO中，
，
∴△CBH≌△BAO（AAS），
∴CH=BO=2，BH=AO=5，
∴OH=7，
∴点C的坐标为（-2，7）； ………（7分）
（3）过点D作DQ⊥x轴于Q，则∠DQP=90°，同（2）可证△ADQ≌△BAO，
∴AQ=BO=2，DQ=AO，
∵AE=AO，
∴DQ=AE，
∵AE⊥AO，
∴∠DQP=∠EAP=90°，
在△DQP和△EAP中，
，
∴△DQP≌△EAP（AAS），
∴QP=AP，
∴AP=AQ=1． ………（12分）