人教A版 (2019)选择性必修 第一册3.2 双曲线综合训练题

这是一份人教A版 (2019)选择性必修 第一册3.2 双曲线综合训练题，共10页。试卷主要包含了双曲线的定义，双曲线的标准方程，求双曲线方程的方法，双曲线的实际应用题等内容，欢迎下载使用。

知识点一 双曲线的定义
1．定义
平面内与两个定点，的距离的差的绝对值等于常数(小于)的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．
2．双曲线定义的集合表示
设点是双曲线上任意一点，则双曲线就是集合．
对于双曲线的定义，有以下理解:
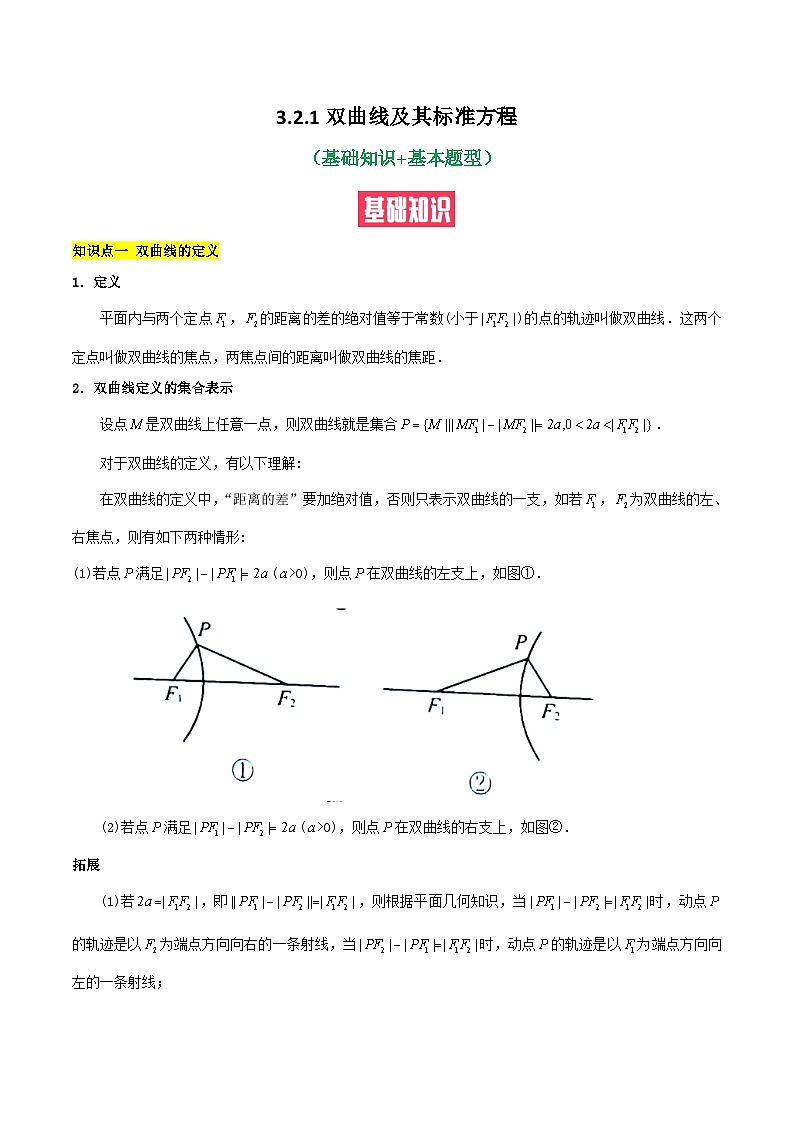
在双曲线的定义中，“距离的差”要加绝对值，否则只表示双曲线的一支，如若，为双曲线的左、右焦点，则有如下两种情形:
(1)若点满足(>0)，则点在双曲线的左支上，如图①．
(2)若点满足(>0)，则点在双曲线的右支上，如图②．
拓展
(1)若，即，则根据平面几何知识，当时，动点的轨迹是以为端点方向向右的一条射线，当时，动点的轨迹是以为端点方向向左的一条射线；
(2)若，即，则与“三角形两边之差小于第三边”相矛盾，故此时动点的轨迹不存在；
(3)特别地，当2=0时，，根据线段垂直平分线的性质，动点的轨迹是线段的垂直平分线．
知识点二 双曲线的标准方程
1．焦点在轴上的双曲线的标准方程为(>0，>0)，焦点分别是，．
焦点在轴上的双曲线的标准方程为(>0，>0)，焦点分别是，．
2．，，三者的关系为．
在双曲线的标准方程中，因为，，三个量满足，所以长度分别为，，的三条线段恰好构成一个直角三角形，且长度为的线段是斜边，如图所示．
提示
(1)标准方程中的两个参数和确定了双曲线的形状和大小，是双曲线的定形条件．
(2)焦点，的位置是双曲线的定位条件，它决定了双曲线标准方程的类型，焦点跟着正项走，即若的系数为正，则焦点在轴上；若的系数为正，则焦点在轴上．
(3)当且仅当双曲线的中心在原点，焦点在坐标轴上时，双曲线的方程才具有标准形式．
(4)双曲线的标准方程的特征是(数Ⅰ与数Ⅱ异号)，因此方程又可写为()，这种形式是当焦点所在的坐标轴不易判断时的统一设法．
椭圆与双曲线的比较如下表：
知识点三 求双曲线方程的方法
拓展
(1)在根据双曲线的定义求标准方程时，要注意动点是满足，还是满足，以便确定是双曲线的两支还是其中一支．
(2)在运用待定系数法求双曲线的标准方程时，要先确定焦点在哪条坐标轴上，若不能确定，则两种形式都讨论．
(3)若已知双曲线上的两点坐标，则通常设方程为，这种设法比设方程为计算更简便，也避免了讨论双曲线的焦点位置．
考点一 双曲线定义的应用
例1 已知双曲线的方程是，点在双曲线上，且到其中一个焦点的距离为10，点是的中点，求的大小(为坐标原点).
解：因为是的中位线
所以，
因为，
，
所以或，
故或．
解双曲线上一点到焦点的距离问题要联想定义，并注意与椭圆的定义加以区别，不能混淆．
例2 如图，已知双曲线的方程为，点均在双曲线的右支上，线段经过双曲线的右焦点，，为双曲线的左焦点，则的周长为( )

A． B． C． D．
解析：由双曲线的定义，知，．
又因为，所以的周长为．
答案：B
应用双曲线定义解题时要根据具体问题，灵活处理绝对值符号，如本例借助双曲线图象直接省略绝对值符号，简化了后面的计算．
例3 如图2．3-4，已知动圆与圆:外切，与圆内切，求动圆圆心的轨迹方程．

分析：利用两圆内切，外切的充要条件找出点所满足的几何关系式，同时结合双曲线定义求解．
解：设动圆的半径为，由已知，得，．
所以，
又因为，，所以，所以，
根据双曲线的定义，知点的轨迹是以，为焦点的双曲线的右支．
因为，所以
所以动圆圆心的轨迹方程为．
(1)在运用双曲线的定义时，应特别注意定义中的条件“差的绝对值”，弄清所求轨迹是双曲线，还是双曲线的一支，若是一支，是哪一支，以确保所求轨迹的纯粹性和完备性．
(2)求曲线的轨迹方程时，应尽量先利用几何条件探求轨迹的曲线类型，再用待定系数法求出曲线的轨迹方程，这样可以减少运算量．
考点二 双曲线的标准方程的应用
例4 求满足下列条件的参数的值或取值范围．
(1)已知，当为何值时，①方程表示双曲线；②表示焦点在轴上的双曲线；③表示焦点在轴上的双曲线；
(2)已知双曲线方程为，焦距为6，求的值；
(3)椭圆与双曲线有相同的焦点，求的值．
解：(1)①若方程表示双曲线，则须满足或
解得或；
②若方程表示焦点在轴上的双曲线，则须满足
解得；
③若方程表示焦点在轴上的双曲线，则须满足
解得．
(2)若焦点在轴上，则方程可化为，
所以，即；
若焦点在轴上，则方程可化为，所以，即．
综上所述，的值为或．
(3)由双曲线方程，知焦点在轴上，且．
由椭圆方程，知，所以，
即，解得或(舍去)．
因此的值为1．
在解题时，首先要确定焦点位置，根据相应的标准方程确定的值，然后求解．有时要注意对焦点在轴，轴上分类讨论，不要漏解．
考点三 双曲线中的焦点三角形问题
例5 已知双曲线上有一点，是双曲线的焦点，且，则的面积为______．
解析:由题意，得．
因为
所以．
所以．
答案：
在解焦点三角形的有关问题时，一般利用两个关系式:
(1)由双曲线的定义，得，的关系式．
(2)利用正弦定理，余弦定理，得，的关系式，求出，的关系式，但是，一般我们不直接求解出，，而是根据需要，把，，看做一个整体来处理．
例6 已知双曲线的两个焦点为，点在双曲线上，若，求点的坐标．
解：由双曲线的方程，知．
不妨设点在第一象限，坐标为，为左焦点，为右焦点，
则
由①，得．所以，所以，
在中，，
所以，代入双曲线的方程，得．即点的坐标是．
再根据双曲线的对称性，得点坐标还可以是，，．
解答本题除了应用双曲线的定义，还应用了数学思想方法中的整体思想:不是求具体的未知数，，而是求整体的值．
考点四 双曲线的实际应用题
例7 某地发生地震，为了援救灾民，救援队在如图2．3-5所示的处收到了一批救灾药品，现要把这批药品沿道路运送到矩形灾民区中去，已知，，，，试在灾民区中确定一条界线，使位于界线一侧的点沿道路送药较近，而另一侧的点沿道路送药较近，请说明这一界线是一条什么曲线，并求出其方程．

分析：审题可得界线是使沿道路和送药一样远近的曲线，设为界线上任一点，则根据已知条件，得，据此设出双曲线的标准方程，用待定系数法求解即可．
解析：灾民区中的点可分为三类，第一类沿道路送药较近，第二类沿道路送药较近，第三类沿道路和送药一样长．依题意，知界线是第三类点的轨迹．设为界线上任一点，则，即(定值)．
因为．
所以界线是以为焦点的双曲线的右支的一部分．如图2．3-6所示，
所在直线为轴，线段的垂直平分线为轴，建立平面直角坐标系．
设所求双曲线的标准方程为．
因为，所以．
故双曲线的标准方程为．
注意到点的坐标为，故的最大值为60，此时．
故界线的曲线方程为．
解决应用问题时，应由题干抽象出数学问题即数学模型，先解决数学问题，再回归到实际应用中．本题由题意能得到所求界线是以为焦点的双曲线，但由于，故所求界线为双曲线的右支．由于没有坐标系，因此需先建立坐标系，并确定方程的形式，再用待定系数法求方程．此题极易忽略和的取值范围．因此在实际问题中，要注意由实际意义确定变量的取值范围．
椭圆
双曲线
定义
与的关系
的关系
标准方程
或
或
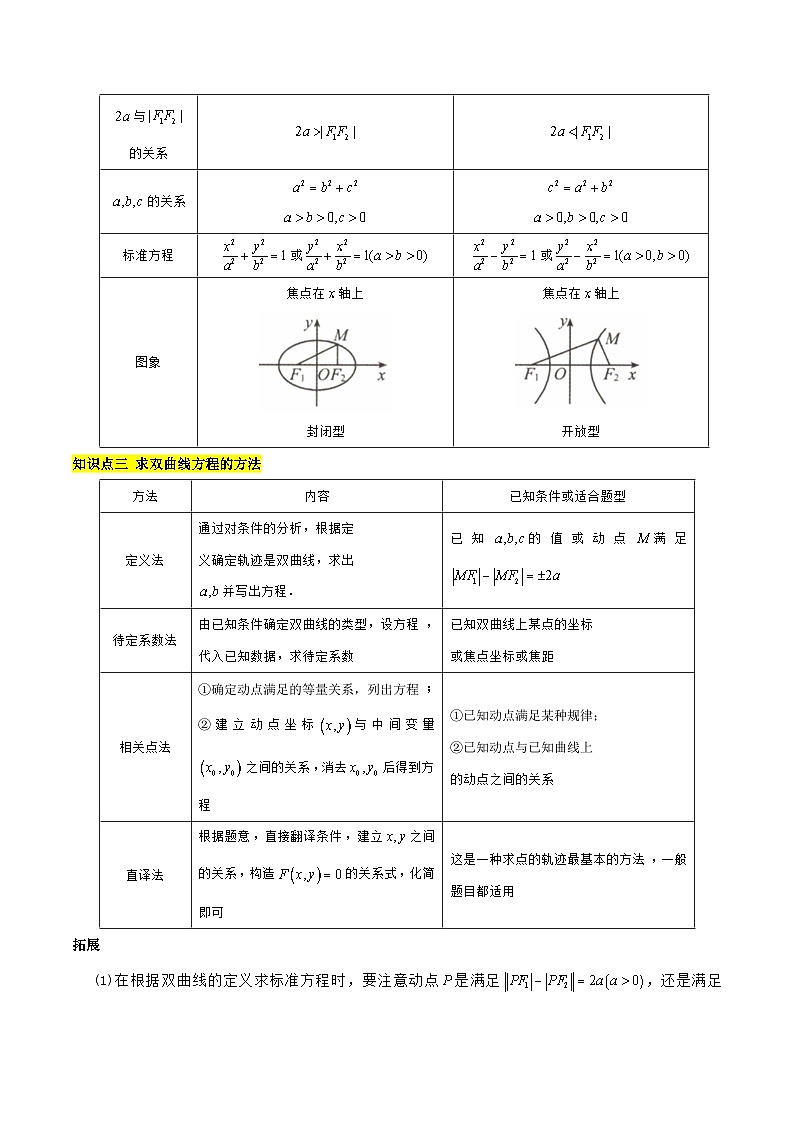
图象
焦点在轴上
封闭型
焦点在轴上
开放型
方法
内容
已知条件或适合题型
定义法
通过对条件的分析，根据定
义确定轨迹是双曲线，求出
并写出方程．
已知的值或动点满足
待定系数法
由已知条件确定双曲线的类型，设方程，代入已知数据，求待定系数
已知双曲线上某点的坐标
或焦点坐标或焦距
相关点法
①确定动点满足的等量关系，列出方程；②建立动点坐标与中间变量之间的关系，消去后得到方程
①已知动点满足某种规律；
②已知动点与已知曲线上
的动点之间的关系
直译法
根据题意，直接翻译条件，建立之间的关系，构造的关系式，化简即可
这是一种求点的轨迹最基本的方法，一般题目都适用