(人教A版必修第二册)高一数学下册同步讲义 专题07 空间直线与平面与平面与平面的平行（课时训练）原卷版+解析

这是一份(人教A版必修第二册)高一数学下册同步讲义 专题07 空间直线与平面与平面与平面的平行（课时训练）原卷版+解析，共39页。

A．BD平面EFGH，且四边形EFGH是矩形
B．EF平面BCD，且四边形EFGH是梯形
C．HG平面ABD，且四边形EFGH是菱形
D．EH平面ADC，且四边形EFGH是平行四边形
2．（2022·浙江·高三专题练习）如图，直三棱柱中，底面三角形是正三角形，E是BC中点，则下列叙述正确的是（ ）
A．与是异面直线B．
C．AE，为异面直线，且D．平面
3．（2021·湖北·高一期末）如图，在下列四个正方体中，为正方体的两个顶点，为所在棱的中点，则在这四个正方体中，直线与平面平行的有（ ）个
①． ②．
③． ④．
A．B．C．D．
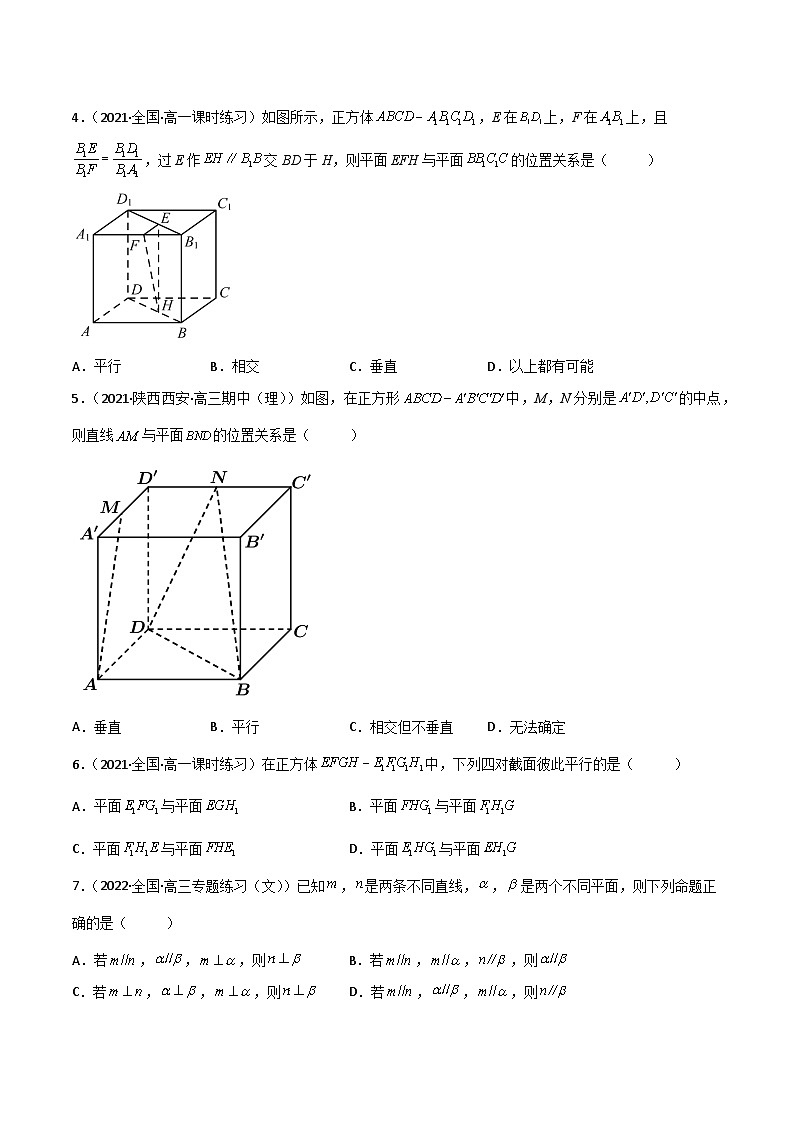
4．（2021·全国·高一课时练习）如图所示，正方体，E在上，F在上，且，过E作交BD于H，则平面EFH与平面的位置关系是（ ）
A．平行B．相交C．垂直D．以上都有可能
5．（2021·陕西西安·高三期中（理））如图，在正方形中，M，N分别是的中点，则直线与平面的位置关系是（ ）
A．垂直B．平行C．相交但不垂直D．无法确定
6．（2021·全国·高一课时练习）在正方体中，下列四对截面彼此平行的是（ ）
A．平面与平面B．平面与平面
C．平面与平面D．平面与平面
7．（2022·全国·高三专题练习（文））已知，是两条不同直线，，是两个不同平面，则下列命题正确的是（ ）
A．若，，，则B．若，，，则
C．若，，，则D．若，，，则
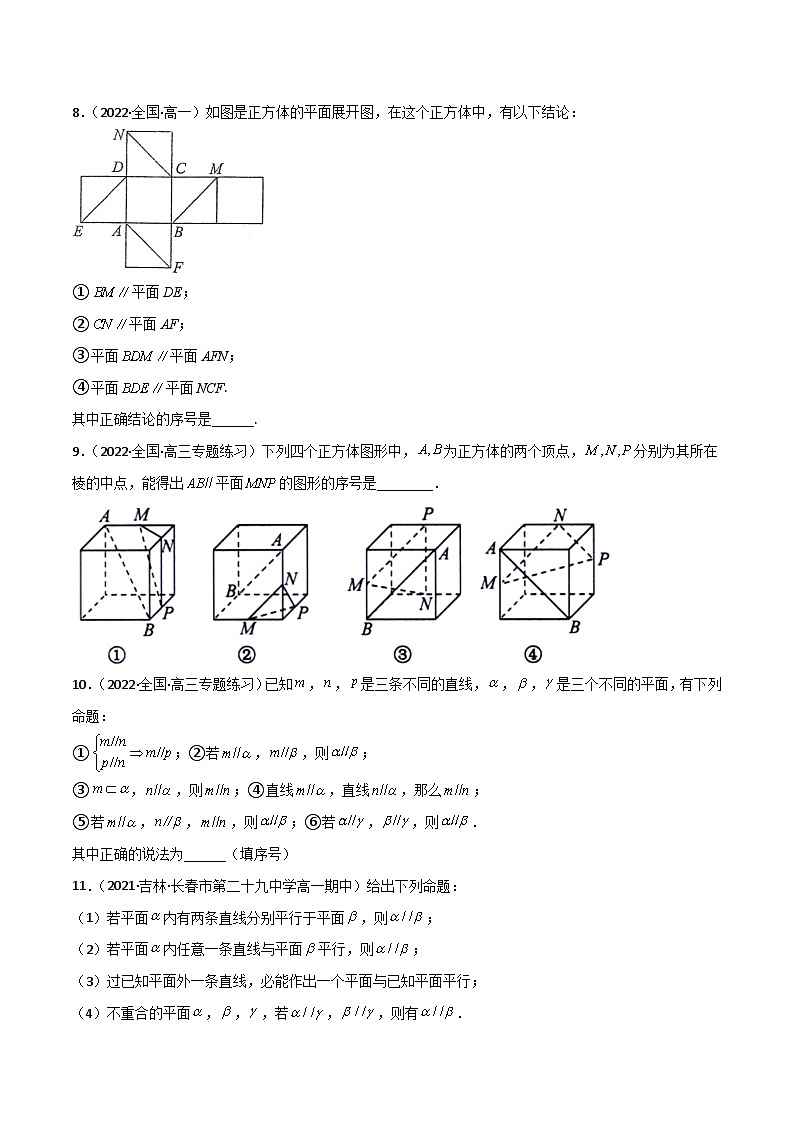
8．（2022·全国·高一）如图是正方体的平面展开图，在这个正方体中，有以下结论：
①平面DE；
②平面AF；
③平面平面AFN；
④平面平面NCF.
其中正确结论的序号是______.
9．（2022·全国·高三专题练习）下列四个正方体图形中，为正方体的两个顶点，分别为其所在棱的中点，能得出平面的图形的序号是________．
10．（2022·全国·高三专题练习）已知，，是三条不同的直线，，，是三个不同的平面，有下列命题：
①；②若，，则；
③，，则；④直线，直线，那么；
⑤若，，，则；⑥若，，则．
其中正确的说法为______（填序号）
11．（2021·吉林·长春市第二十九中学高一期中）给出下列命题：
（1）若平面内有两条直线分别平行于平面，则；
（2）若平面内任意一条直线与平面平行，则；
（3）过已知平面外一条直线，必能作出一个平面与已知平面平行；
（4）不重合的平面，，，若，，则有．
其中正确的命题是_____．（填写序号）
12．（2021·全国·高一课时练习）给出下列说法：
①若直线a∥直线b，a⊂平面α，b⊂平面β，则α∥β；
②若α∥β，直线a与α相交，则a与β相交；
③若l⊂α，m⊂α，且l∥β，m∥β，则α∥β；
④若直线a∥平面β，直线b∥平面α，且α∥β，则a∥b.
其中说法错误的序号是_____.
13．（2021·全国·高一课时练习）下列条件中，能判定平面与平面平行的条件可以是___________.(写出所有正确条件的序号)
①内有无穷多条直线都与平行；
②内的任何一条直线都与平行；
③直线，直线，且，；
④，，.
B组 能力提升
14．（2022·全国·模拟预测）（多选题）如图，在下列四个正方体中，A、B为正方体的两个顶点，M，N，Q分别为所在棱的中点，则在这四个正方体中，直线与平面平行的是（ ）
A．B．
C．D．
15．（2022·浙江杭州·高二期末）（多选题）设α，β为两个平面，则的必要不充分条件是（ ）
A．α内有无数条直线与β平行B．α内有两条相交直线与β平行．
C．α，β垂直于同一条直线D．α，β垂直于同一平面
16．（2021·河北·衡水市冀州区第一中学高三期末）（多选题）如图，在下列四个正方体中，为正方体的两个顶点，为所在棱的中点，则在这四个正方体中，直线与平面不平行的是（ ）
A．B．
C．D．
17．（2021·全国·高一课时练习）（多选题）设a，b是空间中不同的直线，是不同的平面，则下列说法正确的是（ ）
A．若，则
B．若，则
C．若，则
D．若，则
18．（2021·广东·仲元中学高二开学考试）（多选题）如图，在下列四个正方件中，A，B为正方件的两个顶点，M，N，P为所在棱的中点，则在这四个正方体中，直线与平面平行的是( )
A．B．
C．D．
19．（2022·湖南·高一课时练习）如图，四棱锥中，O为底面平行四边形DBCE对角线的交点，F为AE的中点．求证：平面DCF．
20．（2022·全国·高三专题练习）如图，在长方体中，，点是的中点，在上，且.若过的平面交于，交于.
(1)求证：平面；
(2)若，求多面体的体积.
21．（2022·河南·模拟预测（文））如图，直四棱柱的底面为菱形，，，，分别为，的中点．
(1)证明：平面；
(2)平面将该直四棱柱分成两部分，记这两部分中较大的体积为，较小的体积为，求的值．
22．（2022·河南·高三开学考试（文））如图，在三棱柱中，平面平面，四边形是正方形，四边形是矩形，，分别是，的中点.
(1)证明：平面；
(2)若，求点到平面的距离.
23．（2021·全国·高一课时练习）如图在正方体 中，分别是的中点，求证
（1）∥平面；
（2）平面∥平面.
24．（2022·全国·高三专题练习）如图，在多面体ABCDEF中，ABCD是正方形，AB=2，DE=BF=4，BFDE，M为棱AE的中点.求证：平面BMD平面EFC.
25．（2021·全国·高一课时练习）在三棱柱中，
（1）若分别是的中点，求证：平面平面.
（2）若点分别是上的点，且平面平面，试求的值．
专题08 空间直线与平面、平面与平面的平行
A组 基础巩固
1．（2022·湖南·高一课时练习）如图所示，在空间四边形ABCD中，E，F分别为边AB，AD上的点，且AE∶EB＝AF∶FD＝1∶4，又H，G分别为BC，CD的中点，则（ ）
A．BD平面EFGH，且四边形EFGH是矩形
B．EF平面BCD，且四边形EFGH是梯形
C．HG平面ABD，且四边形EFGH是菱形
D．EH平面ADC，且四边形EFGH是平行四边形
【答案】B
【解析】
【分析】
先判断四边形EFGH的形状，再去判断线面是否平行即可解决.
【详解】
△ABD中，AE∶EB＝AF∶FD＝1∶4，则EFBD，且
△BCD中，，则HGBD，且
则，则四边形EFGH是梯形.故选B.
下面看四个平行的判断是否正确.
平面,平面，则BD平面EFGH.判断正确；
平面,平面，则EF平面BCD.判断正确；
平面,平面，则HG平面ABD.判断正确；
梯形EFGH中，，与的延长线会交于一点，则直线EH与平面ADC的位置关系为相交.
故选：B
2．（2022·浙江·高三专题练习）如图，直三棱柱中，底面三角形是正三角形，E是BC中点，则下列叙述正确的是（ ）
A．与是异面直线B．
C．AE，为异面直线，且D．平面
【答案】C
【解析】
【分析】
对于A、B项:利用异面直线的定义直接判断；
对于C项：直接证明出，所以C正确；
对于D项：由与交线有公共点，即可判断.
【详解】
对于A项，与在同一个侧面中，故不是异面直线，所以A错；
对于B项，由题意知与为异面直线，所以B错；
对于C项，因为，为在两个平行平面中且不平行的两条直线，故它们是异面直线，由底面是正三角形，E是BC中点，根据等腰三角形三线合一可知，结合棱柱性质可知，则，所以C正确；
对于D项，因为所在的平面与平面相交，且与交线有公共点，故平面不正确，所以D项不正确.
故选：C
3．（2021·湖北·高一期末）如图，在下列四个正方体中，为正方体的两个顶点，为所在棱的中点，则在这四个正方体中，直线与平面平行的有（ ）个
①． ②．
③． ④．
A．B．C．D．
【答案】C
【解析】
【分析】
利用线面平行的判定方法逐个分析判断即可
【详解】
对于①，如图取底面中心，连接，由于为棱的中点，所以由三角形中位线定理可得∥，因为与平面相交，所以与平面相交，
对于②，如图连接，因为分别为的中点，所以∥，因为∥，所以∥，因为平面，平面，所以∥平面，
对于③，如图，连接，则∥，因为分别为棱的中点，所以由三角形中位线定理可得∥，所以∥，因为平面，平面，所以∥平面，
对于④，如图，连接，则∥，因为分别为棱的中点，所以由三角形中位线定理可得∥，所以∥，因为平面，平面，所以∥平面，
所以直线与平面平行的有3个，
故选：C
4．（2021·全国·高一课时练习）如图所示，正方体，E在上，F在上，且，过E作交BD于H，则平面EFH与平面的位置关系是（ ）
A．平行B．相交C．垂直D．以上都有可能
【答案】A
【解析】
【分析】
根据面面平行的判定定理：由线线平行推出面面平行.
【详解】
在平面中，因为，所以，
由正方体，，所以，
又因为，平面，平面，
平面，平面，，，
所以平面EFH//平面
故选: A.
5．（2021·陕西西安·高三期中（理））如图，在正方形中，M，N分别是的中点，则直线与平面的位置关系是（ ）
A．垂直B．平行C．相交但不垂直D．无法确定
【答案】B
【解析】
【分析】
连接，设，连接，证明四边形为平行四边形可得,从而即可证明平面.
【详解】
解：连接，设，连接，
因为在正方形中，M，N分别是的中点，
所以，且，又
所以，且，
所以四边形为平行四边形，
所以,
因为平面，平面，
所以平面，
故选：B.
6．（2021·全国·高一课时练习）在正方体中，下列四对截面彼此平行的是（ ）
A．平面与平面B．平面与平面
C．平面与平面D．平面与平面
【答案】A
【解析】
【分析】
根据正方体的平行关系，可证平面与平面平行，可得出结论.
【详解】
如图，正方体，
所以四边形是平行四边形，平面，
面，所以平面，同理平面.
因为平面，
所以平面平面.
故选：A
7．（2022·全国·高三专题练习（文））已知，是两条不同直线，，是两个不同平面，则下列命题正确的是（ ）
A．若，，，则B．若，，，则
C．若，，，则D．若，，，则
【答案】A
【解析】
【分析】
根据题目条件结合模型找反例即可求解.
【详解】
A.两条不同的直线同时垂直两个平行的平面，所以这两条直线平行，故A正确；
B.若，相交，且分别平行于，的交线，也满足条件，故错误；
C. 若，，，此时可以 故错误；
D. 若，，，此时可以，故错误.
故选A.
8．（2022·全国·高一）如图是正方体的平面展开图，在这个正方体中，有以下结论：
①平面DE；
②平面AF；
③平面平面AFN；
④平面平面NCF.
其中正确结论的序号是______.
【答案】①②③④.
【解析】
【分析】
将图形还原为正方体，进而根据点线面的位置关系及线面平行和面面平行的判定定理判断答案.
【详解】
如图，
对①，因为，所以四边形是平行四边形，所以，而平面DE，平面DE，则平面DE.正确；
对②，因为，所以四边形是平行四边形，所以，而平面AF，平面AF，则平面AF.正确；
对③，因为，所以四边形是平行四边形，所以，
又因为，所以四边形是平行四边形，所以，而，所以平面BDM∥平面AFN.正确；
对④，因为，所以四边形是平行四边形，所以，同由③：，而，所以平面平面NCF.正确.
故答案为：①②③④.
9．（2022·全国·高三专题练习）下列四个正方体图形中，为正方体的两个顶点，分别为其所在棱的中点，能得出平面的图形的序号是________．
【答案】①④
【解析】
【分析】
证明所在的平面与平面平行可判断①；若下底面中心为，连接，可得可判断②；由面可判断③；证明可判断④，进而可得正确答案.
【详解】
在①中：如图：因为分别为其所在棱的中点，所以，，
因为面，面，所以面，同理可得面，
因为，所以面面，因为面，所以平面，故①成立；
在②中，若下底面中心为，连接，可得，面，所以与平面不平行，故②不成立；
在③中：如图：平面即为平面，因为面，所以与面不平行，故③不成立；
在④中：如图：且，所以四边形是平行四边形，可得，因为，所以，因为面，面，
所以所以平面，故④成立．
故答案为：①④.
10．（2022·全国·高三专题练习）已知，，是三条不同的直线，，，是三个不同的平面，有下列命题：
①；②若，，则；
③，，则；④直线，直线，那么；
⑤若，，，则；⑥若，，则．
其中正确的说法为______（填序号）
【答案】①⑥
【解析】
【分析】
利用线线平行、线面平行、面面平行的判定和性质应用，逐一判断选项可得结论.
【详解】
解：对于①，根据平行的性质有：，即，故①正确；
对于②，由得或相交，故②错误；
对于③，由得，或异面，故③错误；
对于④，由直线，直线，可得，异面，相交，故④错误；
对于⑤，由，得或相交，故⑤错误；
对于⑥，若，由面面平行的传递性得，故⑥正确，
故答案为：①⑥.
11．（2021·吉林·长春市第二十九中学高一期中）给出下列命题：
（1）若平面内有两条直线分别平行于平面，则；
（2）若平面内任意一条直线与平面平行，则；
（3）过已知平面外一条直线，必能作出一个平面与已知平面平行；
（4）不重合的平面，，，若，，则有．
其中正确的命题是_____．（填写序号）
【答案】（）（）
【解析】
【分析】
由平面与平面平行的判定判断（1）；由平面与平面平行的定义判断（2）与（3）；由平面平行的传递性判断（4）．
【详解】
解：（1）由平面与平面平行的判定可知，若平面内有两条相交直线分别平行于平面，则，故（1）错误；
（2）由平面与平面平行的定义可知，若平面内任意一条直线与平面平行，则，故（2）正确；
（3）当平面外的一条直线与平面相交时，过已知平面外一条直线，不能作出一个平面与已知平面平行，故（3）错误；
（4）不重合的平面，，，若，，由平面与平面平行的传递性可得，故（4）正确．
故答案为：（2）（4）．
12．（2021·全国·高一课时练习）给出下列说法：
①若直线a∥直线b，a⊂平面α，b⊂平面β，则α∥β；
②若α∥β，直线a与α相交，则a与β相交；
③若l⊂α，m⊂α，且l∥β，m∥β，则α∥β；
④若直线a∥平面β，直线b∥平面α，且α∥β，则a∥b.
其中说法错误的序号是_____.
【答案】①③④
【解析】
【分析】
利用空间中线线，线面，面面的位置关系逐一判断即可
【详解】
对于①，α，β可能相交，故①错误.
对于②，假设直线a与平面β平行或直线a⊂β，则由平面α∥平面β，知a⊂α或a∥α，这与直线a与α相交矛盾，所以a与β相交，故②正确.
对于③，当l∥m时，α，β可能相交，故③错误.
对于④，a与b平行、相交或异面都有可能，故④错误.
故答案为：①③④
13．（2021·全国·高一课时练习）下列条件中，能判定平面与平面平行的条件可以是___________.(写出所有正确条件的序号)
①内有无穷多条直线都与平行；
②内的任何一条直线都与平行；
③直线，直线，且，；
④，，.
【答案】②④
【解析】
【分析】
利用平面与平面的位置关系判断.
【详解】
当内有无穷多条直线都与平行，平面与平面可能平行，也可能相交，故①不正确.
当内的任何一条直线都与平行时，则平面内必有2条相交直线和平面平行，据面面平行的判定定理，平面与平面平行，故②正确.
当直线，直线，且，时，平面与平面可能平行，也可能相交，故③不正确.
当，，时，可证，这样，平面与平面都和直线垂直，故平面与平面平行，故④正确.
综上，②④正确，①③错误，
故答案为：②④.
B组 能力提升
14．（2022·全国·模拟预测）（多选题）如图，在下列四个正方体中，A、B为正方体的两个顶点，M，N，Q分别为所在棱的中点，则在这四个正方体中，直线与平面平行的是（ ）
A．B．
C．D．
【答案】ABC
【解析】
【分析】
由线面平面平行的判定定理可判断选项A,B,C；由平面平面，可判断选项D.
【详解】
A选项中，，平面，平面，所以直线与平面平行，所以选项A正确；
B，C选项中，，平面，平面，所以直线与平面平行，所以选项B，C正确；
D选项中，如图在正方体中，，平面,平面,则平面
，平面,平面,则平面
又，所以平面平面
又平面，所以直线与平面相交
所以直线与平面不平行，所以选项D错误.
故选：ABC
15．（2022·浙江杭州·高二期末）（多选题）设α，β为两个平面，则的必要不充分条件是（ ）
A．α内有无数条直线与β平行B．α内有两条相交直线与β平行．
C．α，β垂直于同一条直线D．α，β垂直于同一平面
【答案】AD
【解析】
【分析】
要判断是否为的必要不充分条件，就要依据的是能推出该条件，但该条件不能推出，据此一一判断即可.
【详解】
A，时α内一定有无数条直线与β平行，但α内有无数条直线与β平行时，除外，两平面还可能相交，故A是必要不充分条件；
B，α内有两条相交直线与β平行，那么根据线面平行的判定定理可知，故B不是必要不充分条件；
C, α，β垂直于同一条直线，则能得出，故C不是必要不充分条件；
D, α，β垂直于同一平面，两平面可能相交，推不出，但时，一定会有α，β垂直于同一平面，故D是必要不充分条件.
故选：AD.
16．（2021·河北·衡水市冀州区第一中学高三期末）（多选题）如图，在下列四个正方体中，为正方体的两个顶点，为所在棱的中点，则在这四个正方体中，直线与平面不平行的是（ ）
A．
B．
C．
D．
【答案】BC
【解析】
【分析】
根据线面平行的判定定理，结合反证法，逐一分析各个选项，即可得答案.
【详解】
对于A：连接CD，如图所示：
因为M、Q分别为所在棱的中点，
所以，
又，
所以，
又平面，平面，
所以平面，故A错误.
对于B：连接BC、DE，设，连接QO，如图所示：
因为Q、O分别为所在棱的中点，
所以，
又平面，即直线与平面不平行，
所以直线与平面不平行，故B正确；
对于C：假设平面，
因为N、Q为所在棱的中点，
所以，如图所示
所以平面平面MNQ，与该几何体为正方体矛盾，
所以假设不成立，即直线与平面不平行，故C正确.
对于D：因为M、N为所在棱的中点，
所以，如图所示
又，
所以，
又平面，平面，
所以平面，故D错误.
故选：BC
17．（2021·全国·高一课时练习）（多选题）设a，b是空间中不同的直线，是不同的平面，则下列说法正确的是（ ）
A．若，则
B．若，则
C．若，则
D．若，则
【答案】AD
【解析】
【分析】
根据线面平行和面面平行的判定方法和性质验证每一个选项即可﹒
【详解】
在选项A中，，由线面平行判定定理得，，故A项正确；
在选项B中，，则a与b平行或异面，故B项错误；
在选项C中，，则与相交或平行，故C项错误；
在选项D中，由面面平行的性质定理得D项正确．
故选：AD﹒
18．（2021·广东·仲元中学高二开学考试）（多选题）如图，在下列四个正方件中，A，B为正方件的两个顶点，M，N，P为所在棱的中点，则在这四个正方体中，直线与平面平行的是( )
A．B．
C．D．
【答案】AC
【解析】
【分析】
对于选项A：结合已知条件利用线线平行证明面面平行，然后利用面面平行的性质证明线面平行；对于选项BD：利用线线的位置关系即可判断线面的位置关系；对于选项C：利用线面平行的判定定理即可求解.
【详解】
对于A选项：过A作正方体的面对角线，且，如下图所示：
由已知条件可知，，
又因为，，
所以平面平面，
又因为平面，所以平面，故A正确；
对于B选项：连接正方体底面对角线BC和EF，相交于O，且BC与MP交于H，连接ON，
如下图所示：
由上图可知，O为的中点，故，
因为与平面相交，所以也与平面相交，故B错误；
对于选项C：连接NP所在面的正方体的面对角线EF，且，如下图所示：
由已知条件和正方体的结构特征可知，，
因为平面，平面，
所以平面，故C正确；
对于选项D：连接NP所在面的正方体的面对角线EF，且，如下图所示：

因为EF和NP相交，且平面，所以EF和平面相交，
从而与平面相交，故D错误.
故选：AC.
19．（2022·湖南·高一课时练习）如图，四棱锥中，O为底面平行四边形DBCE对角线的交点，F为AE的中点．求证：平面DCF．
【答案】证明见解析
【解析】
【分析】
以线面平行判定定理去证明即可.
【详解】
连接OF
O为底面平行四边形DBCE对角线的交点，则
△中，，，则
又平面，平面，则平面DCF．
20．（2022·全国·高三专题练习）如图，在长方体中，，点是的中点，在上，且.若过的平面交于，交于.
(1)求证：平面；
(2)若，求多面体的体积.
【答案】(1)证明见解析
(2)
【解析】
【分析】
（1）由面面平行的性质可证，进而得证；
（2）连接，将多面体分割成两个四棱锥，分别求解两四棱锥体积，即可求解.
(1)
长方体
平面平面，
交长方体于，
，
又平面，平面，
平面
(2)
由面面平行性质，可得，
四边形为平行四边形，
过点分别向､作垂线，交点分别为､
过点向作垂线，交点为
由长方体中，
可得，故
点是的中点，，
结合立体图形可得：
四边形为棱形
同理可证：，可得，
进而可得
为中点，连接
将多面体分割成两个四棱锥和
由几何关系知，
，
多面体.
21．（2022·河南·模拟预测（文））如图，直四棱柱的底面为菱形，，，，分别为，的中点．
(1)证明：平面；
(2)平面将该直四棱柱分成两部分，记这两部分中较大的体积为，较小的体积为，求的值．
【答案】(1)证明见解析
(2)
【解析】
【分析】
（1）连接，交于点，根据中位线定理，和平行线的传递性，可得，且，即可证四边形为平行四边形，可得，再根据线面平行的判定定理，即可证明结果；
（2）延长，交于点，根据题意可知平面将该直四棱柱分成两部分中体积较小的部分为三棱台．根据三棱台的体积等于三棱锥的体积减去三棱锥的体积，可求出；再根据直棱柱体积公式即可求出的体积，进而求出，由此即可求出．
(1)
证明：连接，交于点，连接，，
因为，分别为，的中点，所以，且，
因为为的中点，所以，且，
所以，且，所以四边形为平行四边形，所以，
因为平面，平面，故平面．
(2)
解：延长，交于点，
则，分别为，的中点，，，
再连接，交于点，则为的中点，，连接，
所以平面将该直四棱柱分成两部分中体积较小的部分为三棱台．
因为三棱台的体积等于三棱锥的体积减去三棱锥的体积，
所以
．
又直四棱柱的体积为，
所以，故．
22．（2022·河南·高三开学考试（文））如图，在三棱柱中，平面平面，四边形是正方形，四边形是矩形，，分别是，的中点.
(1)证明：平面；
(2)若，求点到平面的距离.
【答案】(1)证明见解析
(2)
【解析】
【分析】
（1）作辅助线证明从而根据线面平行的判定定理证明平面；
（2）先求三棱锥的体积，再求出的面积，根据三棱锥的体积与三棱锥的体积相等即可求得答案.
(1)
证明：如图，连接.
因为四边形是正方形，且是的中点，
所以，，共线，且为的中点.
因为是的中点，所以.
因为平面，平面，所以平面.
(2)
解：因为四边形是正方形，所以.
因为平面平面，且平面平面，
所以平面，
连接，因为，
所以三棱锥的体积为.
因为是的中点，所以三棱锥的体积为.
因为，，，
则的底边上的高为 ,
所以的面积为.
设点到平面的距离为，
因为三棱锥的体积与三棱锥的体积相等，
所以，解得，
即点到平面的距离为.
23．（2021·全国·高一课时练习）如图在正方体 中，分别是的中点，求证
（1）∥平面；
（2）平面∥平面.
【答案】（1）证明详见解析；（2）证明详见解析.
【解析】
【分析】
（1）证得，进而由线面平行的判定定理可证得结果；
（2）由（1）可知，只需证明平面，进而由面面平行的判定定理可证得结果.
【详解】
（1）连接，依题意知，，所以，又平面，平面，所以平面.
（2）连接，依题意可知，且，所以四边形是平行四边形，则，
又平面，平面，所以平面.
由（1）知平面，且，故平面平面.
24．（2022·全国·高三专题练习）如图，在多面体ABCDEF中，ABCD是正方形，AB=2，DE=BF=4，BFDE，M为棱AE的中点.求证：平面BMD平面EFC.
【答案】证明见解析
【解析】
【分析】
连接AC，交BD于点N，则MNEC，根据线面平行的判定有MN平面EFC，由题设知BDEF为平行四边形，即BDEF，根据线面平行的判定有BD平面EFC，结合面面平行的判定证平面BMD平面EFC.
【详解】
证明：如图，连接AC，交BD于点N，
∴N为AC的中点，连接MN，则MNEC.
∵面EFC，面EFC，
∴MN平面EFC.
∵BFDE，BF=DE，
∴四边形BDEF为平行四边形，
∴BDEF.
∵平面EFC，平面EFC，
∴BD平面EFC，又MN∩BD=N，
∴平面BMD平面EFC.
【点睛】
关键点点睛：由中位线、平行四边形的性质确定线线平行，根据线面平行的判定证明线面平行，再由面面平行的判定证明面面平行.
25．（2021·全国·高一课时练习）在三棱柱中，
（1）若分别是的中点，求证：平面平面.
（2）若点分别是上的点，且平面平面，试求的值．
【答案】（1）证明见解析；（2）1.
【解析】
【分析】
（1）先证明平面，在证明平面，即可证明平面平面；
（2）连接交于O，连接，由题意先面面平行的性质证明，再由平行的性质结合题设即可求解
【详解】
（1）∵分别是的中点，
∴，
∵平面，平面，
∴平面，
∵，，
∴四边形是平行四边形，
∴，
又∵平面，平面，
∴平面，
又∵，平面，
∴平面平面；
（2）连接交于O，连接，
由平面平面，且平面平面，
平面平面，
∴，
则，
又由题设，∴，即.