山东省济宁市金乡县2023-2024学年九年级上学期期末数学试题(含答案)

这是一份山东省济宁市金乡县2023-2024学年九年级上学期期末数学试题(含答案)，共20页。试卷主要包含了单选题，四象限，解答题等内容，欢迎下载使用。


一、单选题
1．已知，则下列比例式成立的是（ ）
A．B．C．D．
2．如图是由6个相同的小正方体组成的几何体，其俯视图是（ ）
A．B．C．D．
3．将二次函数化成的形式为（ ）
A．B．C．D．
4．一个不透明的箱子里装有m个球，其中红球有5个，这些球除颜色外都相同．每次将球搅拌均匀后，任意摸出一个球记下颜色后再放回．大量重复试验后发现，摸到红球的频率稳定在0.25，那么可以估算出m的值为（ ）
A．25B．20C．15D．10
5．反比例函数的图象经过点，则下列说法错误的是（ ）
A．B．函数图象分布在第二、四象限
C．当时，y随x的增大而增大D．当时，y随x的增大而减小
6．如图所示，若，则需满足（ ）
A．B．
C．D．
7．在中， ， ，则的值是（ ）
A．B．C．2D．
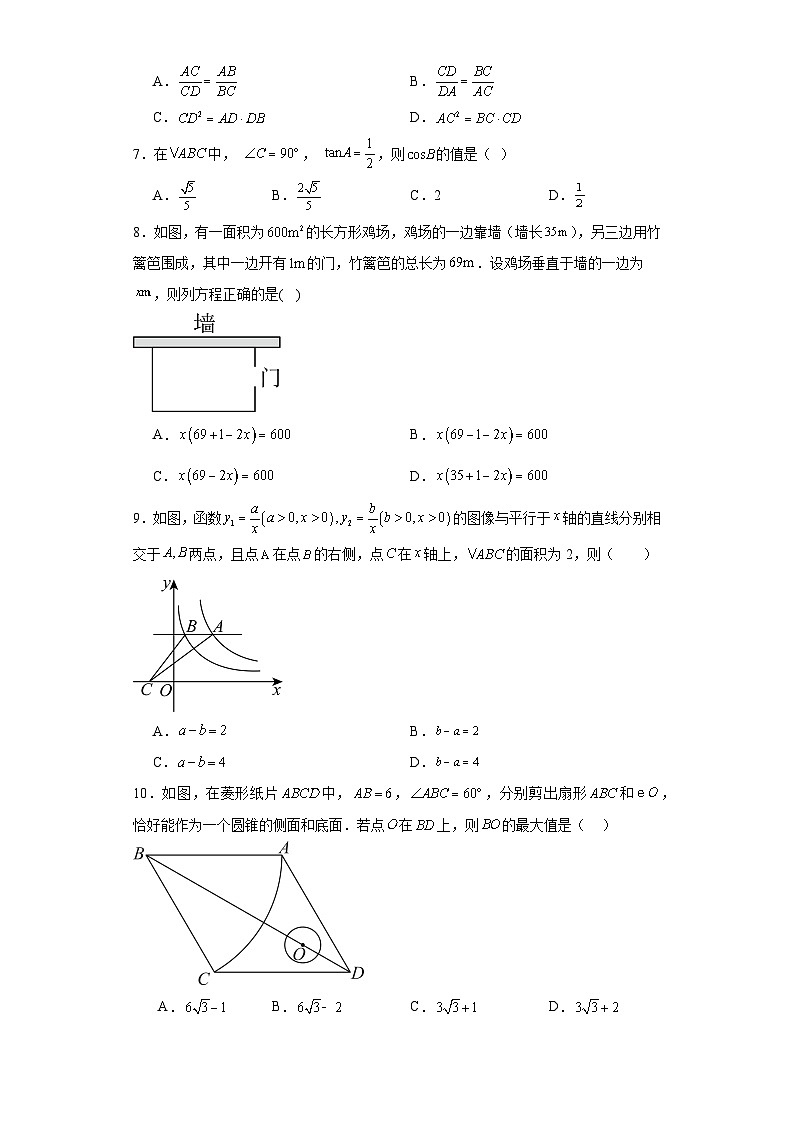
8．如图，有一面积为的长方形鸡场，鸡场的一边靠墙（墙长），另三边用竹篱笆围成，其中一边开有的门，竹篱笆的总长为．设鸡场垂直于墙的一边为，则列方程正确的是( )

A．B．
C．D．
9．如图，函数的图像与平行于轴的直线分别相交于两点，且点在点的右侧，点在轴上，的面积为2，则（ ）

A．B．
C．D．
10．如图，在菱形纸片中，，，分别剪出扇形和，恰好能作为一个圆锥的侧面和底面．若点在上，则的最大值是（ ）
A．B．C．D．
二、填空题
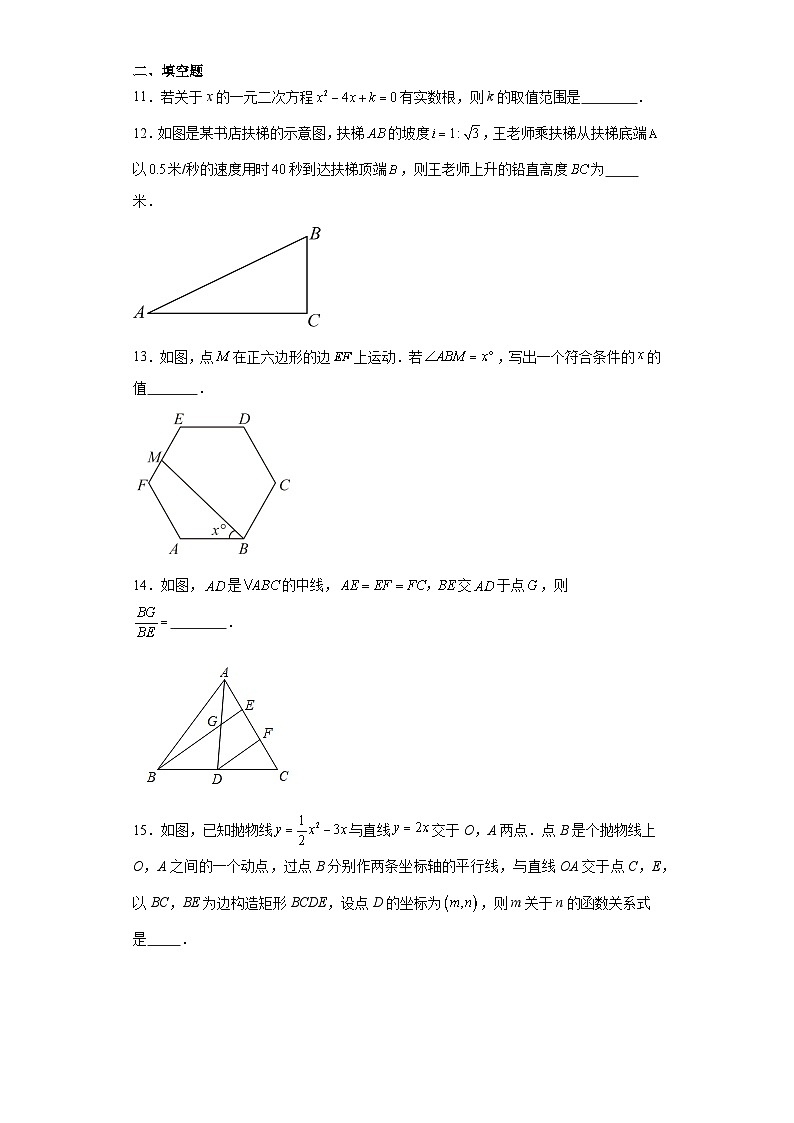
11．若关于x的一元二次方程有实数根，则k的取值范围是 ．
12．如图是某书店扶梯的示意图，扶梯的坡度，王老师乘扶梯从扶梯底端以米/秒的速度用时秒到达扶梯顶端，则王老师上升的铅直高度为 米．

13．如图，点在正六边形的边上运动．若，写出一个符合条件的的值 ．
14．如图，是的中线，交于点，则 ．
15．如图，已知抛物线与直线交于O，A两点．点B是个抛物线上O，A之间的一个动点，过点B分别作两条坐标轴的平行线，与直线OA交于点C，E，以BC，BE为边构造矩形BCDE，设点D的坐标为，则m关于n的函数关系式是 ．
三、解答题
16．计算：．
17．为了解学生参加学校社团活动的情况，对报名参加A：篮球，B：舞蹈，C：书法，D：田径，E：绘画这五项活动的学生（每人必选且只能参加一项）中随机抽取了部分学生进行调查，并将调查结果绘制成如下两幅不完整的统计图．
根据所给的信息，解答下列问题：
(1)这次被调查的学生共有___________人，并把条形统计图补充完整；
(2)若该校共有名学生参加社团活动，请你估计这名学生中约有多少人参加书法社团；
(3)在田径社团活动中，由于甲，乙，丙，丁四人平均的成绩突出，现决定从他们中任选两名参加区级运动会．用树状图或列表的方法求恰好选中甲，乙两位同学参加的概率．
18．如图，三角形中，为中点，，，以为直径作圆，恰好与相切于点．求：

(1)圆的半径；
(2)连接，交于，求的长度；
19．莲花湖湿地公园是当地人民喜爱的休闲景区之一，里面的秋千深受孩子们喜爱．如图所示，秋千链子的长度为，当摆角恰为时，座板离地面的高度为，当摆动至最高位置时，摆角为，求座板距地面的最大高度为多少？（结果精确到；参考数据：，，，，，）

20．如图，已知矩形的两个顶点A，B都在反比例函数的图象上，经过原点O，对角线垂直于x轴．垂足为E，已知点A的坐标为．

(1)求反比例函数的解析式；
(2)求矩形的面积．
21．红布李（李子的一种）含有丰富的营养成分，并且具有养生和美颜的功效，所以自古就被冠以“五果之首”，深受人们的喜爱，光明村种植有大片的红布李，某“乡村振兴”电商平台为光明村农户销售红布李，运营成本为每千克3元，除去运营成本余下的收入都归农户所有，在销售过程中要求农户的保底收入为3元/千克，且售价不超过15元/千克.市场调查发现，每周的红布李销售量y（千克）与售价x（元/千克）（x为正整数）之间满足某种函数关系如图所示.
(1)请直接写出y与x之间的函数关系式，并注明x的取值范围；
(2)求当红布李的售价为多少元时，光明村农户一周的收入最大?最大收入是多少元?
(3)今年七月下旬天晴少雨，气温持续在上下，红布李成熟非常快，根据光明村这一时期红布李的产量，一周的销售量不少于6000千克，求本周光明村农户获得的最大收入和红布李售价分别为多少元?
22．（1）如图①，在中，，将绕点C逆时针旋转，得到，连接，求的大小；
（2）如图②，在中，，将绕点C逆时针旋转得到，连接，以为圆心，长为半径作圆，猜想直线与的位置关系，并证明你的结论：
（3）如图③，，，将绕点C逆时针旋转得到，连接和，求的面积.
图① 图② 图③
参考答案：
1．B
【分析】根据比例的基本性质进行判断即可．
【详解】解：∵，
∴，，，
则A、C、D选项均不正确，B正确，
故选：B
【点睛】此题考查了比例的基本性质，熟练掌握比例的基本性质并灵活变形是解题的关键．
2．D
【分析】对照几何体得到视图A、B、C、D分别是从左边，前边，右边，上边看到的图形，即得．
本题主要考查了俯视图，解决问题的关键是熟练掌握主视图，左视图，俯视图分别是从物体的前边，左边，上边看到的图形．
【详解】A、 是从左边看到的图形；
B、 是从前边看到的图形；
C、 是从右边看到的图形；
D、 是从上面边看到的图形．
故选：D．
3．B
【分析】利用配方法将二次函数的一般式化成顶点式即可．
【详解】解：
，
故选B．
【点睛】本题考查了二次函数的顶点式，熟练掌握配方法是解题的关键．
4．B
【分析】用红球的数量除以红球的频率即可．
【详解】解：（个，
所以可以估算出的值为20，
故选：B．
【点睛】本题考查利用频率估计概率，解题的关键是掌握在大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．
5．D
【分析】根据题意求得反比例函数的解析式，根据的值，判断函数的图象所在象限以及增减性即可求解．
【详解】解：∵反比例函数的图象经过点，
∴，故A选项正确，不符题意；
∵，
∴反比例数的图象分布在第二、四象限，故B选项正确，不符题意；
在每一个象限内，函数值随的增大而增大，故C选项正确，D选项不正确，
故选：D．
【点睛】本题考查了反比例函数图象的性质，求得的值是解题的关键．
6．D
【分析】本题主要考查了相似三角形的判定，熟知相似三角形的判定定理是解题的关键．
【详解】解：由，即，结合条件，可证明，
根据现有条件由A、B、C三个选项中的结论都不能证明，
故选：D．
7．B
【分析】本题考查了同角三角函数的关系，先根据题意画出直角三角形，设，求出及，然后可得出的值．
【详解】解：如图：
∵，
∴可以假设，，
∴
∴，
故选：B．
8．A
【分析】求出平行于墙的一边的长度，即可建立一元二次方程．
【详解】解：∵鸡场垂直于墙的一边为 xm ，
∴平行于墙的一边的长度为：m
∴
故选：A
【点睛】本题考查图形与一元二次方程．正确理解题意是解题关键．
9．C
【分析】本题考查了反比例函数的性质、反比例函数图像上点的坐标特征，根据函数的特征设，，再根据进行求解是解决问题的关键．
【详解】解：由题意可设，，
则，
∴，
故选：A．
10．B
【分析】根据已知条件求得的半径为，进而求得，当与相切时，取得最大值，根据含度角的直角三角形的性质求得，即可求解．
【详解】解：∵，，
∴的长为，
∴的半径为，
连接，则是等边三角形，，
∴
当与相切时，取得最大值，
设与相切于点，则
∵在菱形纸片中，，
∴，
∴
∴的最大值是，
故选：B．
【点睛】本题考查了菱形的性质，圆锥侧面积公式，切线的性质，勾股定理，综合运用以上知识是解题的关键．
11．
【分析】本题主要考查了根的判别式，掌握一元二次方程的根与有如下关系：当时，方程有两个不相等的实数根；当时，方程有两个相等的实数根；当时，方程无实数根．利用根的判别式列不等式求解即可．
【详解】解：根据题意得：，解得：．
故答案为：．
12．
【分析】本题考查的是解直角三角形的应用—坡度坡角问题，掌握坡度是坡面的铅直高度h和水平宽度l的比是解题的关键．
【详解】解：由题可知米，
设，则，
根据勾股定理得到：，
即，
解得：，（舍去）
∴王老师上升的铅直高度为米，
故答案为：10．
13．（答案不唯一）
【分析】先求得，在根据点的不同位置，求得的取值范围，从而得解．
【详解】解：∵六边形是正六边形，
∴，，
当点在点处时，
∵，，
∴，
当点在点处时，延长交的延长线于点，
∵，，
∴，
∴，
∴是正三角形，
∴，
∵，，
∴即，
∴是正三角形，
∴，
∴，
故答案为（答案不唯一）．
【点睛】本题主要考查了正多边形的性质，等边三角形的判定及性质，三角形的内角和定理，熟练掌握正多边形的性质，等边三角形的判定及性质是解题的关键．
14．
【分析】先证得为的中位线，可得，从而得到，进而得到，可得到，即可求解．
【详解】解：∵，
∴点F为的中点，
∵是的中线，
∴为的中位线，
∴，
∴，
∴，
即，
∴，
∴．
故答案为：
【点睛】本题考查相似三角形的判定和性质，三角形中位线性质，掌握相似三角形的判定和性质，三角形中位线性质的应用是解题关键．
15．
【分析】据点D的坐标，可得出点E的坐标，点C的坐标，继而确定点B的坐标，将点B的坐标代入抛物线解析式可求出m，n之间的关系式．
【详解】解：∵直线OA的解析式为：y=2x，
点D的坐标为（m，n），
∴点E的坐标为（n，n），点C的坐标为（m，2m），
∴点B的坐标为（n，2m），
把点B（n，2m）代入，
可得：，
故答案为：．
【点睛】本题考查了二次函数的综合，矩形的性质，函数图象上点的坐标特征，解答本题需要同学们能理解矩形四个顶点的坐标之间的关系．
16．
【分析】先计算零指数幂，负整数指数幂，化简二次根式，特殊角三角函数值，再根据实数的混合计算法则求解即可．
【详解】解：原式
．
【点睛】本题主要考查了实数的混合计算，化简二次根式，特殊角三角函数值，零指数幂和负整数指数幂，熟知相关计算法则是解题的关键．
17．(1)，图见解析
(2)
(3)，图见解析
【分析】（1）用篮球人数除以所占百分比即可求出调查的学生总人数，用总人数减去除田径外其他项目的人数即可得到参加田径的人数，然后补充条形统计图即可；
（2）先计算出参加书法社团的百分比，然后用相乘即可；
（3）画出树状图，然后根据树状图计算概率即可．
【详解】（1）解：被调查的学生共有（人），
参加田径的人数为（人），
条形统计图补充完整如下图所示，
（2）解：（人），
答：这名学生中约有人参加书法社团．
（3）解：如图所示，
由图可知，甲乙两位同学参加有种情况，总共有种情况，
则恰好选中甲，乙两位同学参加的概率为．
【点睛】本题考查了条形统计图与扇形统计图综合，树状图与概率计算，掌握相关知识并正确计算是解题关键．
18．(1)
(2)
【分析】（1）连接，则，设半径为，则中，勾股定理得，从而可得答案；
（2）证明，可得，可得，由垂直平分，证明，可得，证明，可得为中点，因为，可得，从而可得答案．
【详解】（1）解：连接，以为直径作圆，恰好与相切于点，
∴，

∵为中点，，
∴，
设半径为，则，
∴．
（2）如图，连接，，交于点P，由（1）可得：，，，
∴，
∴，

∴，
∵，，
∴，，
∴，而，，
∴，
∴，，
∴，
∴，
∴．
【点睛】本题考查的是全等三角形的判定与性质，勾股定理的应用，切线的性质，三角形的外角的性质，锐角三角函数的应用，掌握以上基础知识是解本题的关键．
19．座板距地面的最大高度为．
【分析】过点A作于点D，过点A作于点E，过点B作于点F，利用和的余弦值求出，，然后利用线段的和差和矩形的性质求解即可．
【详解】如图所示，过点A作于点D，过点A作于点E，过点B作于点F，

由题意可得，四边形和四边形是矩形，
∴，，
∵秋千链子的长度为，
∴，
∵，，
∴，
∴，
∵，，
∴，
∴，
∴．
∴座板距地面的最大高度为．
【点睛】本题考查解直角三角形的应用，解题的关键是明确题意，利用数形结合的思想解答问题．
20．(1)
(2)10
【分析】（1）把代入，即可求解；
（2）根据中心对称的性质得，根据勾股定理得到，根据相似三角形的性质和矩形的面积公式即可得到结论．
【详解】（1）解：把代入得，
，
反比例函数的解析式为；
（2）解：点的坐标为，
根据中心对称可得，
，
对角线垂直于轴，
∴，
∵，
，
，
，
，
矩形的面积为．
【点睛】本题考查了待定系数法求函数的解析式，矩形的面积的计算，中心对称图形的性质，相似三角形的判定与性质，正确地求出函数的解析式是解题的关键．
21．(1)，
(2)当红布李的售价为元时，光明村农户一周的收入最大，最大收入是55125元
(3)本周光明村农户获得的最大收入和红布李售价分别为54000元和12元
【分析】本题考查了一次函数和二次函数的应用，一元一次不等式的实际应用，熟练掌握待定系数法以及二次函数的性质是解题的关键．
（1）利用待定系数法求出函数解析式，再根据题意求出x的取值范围即可；
（2）设本周光明村农户一周获得的收入为w元，根据题意列出w关于x的二次函数解析式，然后利用二次函数的性质解答；
（3）设本周光明村农户获得的收入为w元，根据题意列出w关于x的二次函数解析式，然后利用二次函数的性质解答．
【详解】（1）解：设，
把代入得：，
解得：，
∴，
∵平台的运营成本为每千克3元，农户的保底收入为每千克3元，且售价不超过15元/千克，
∴；
（2）解：设光明村农户一周获得的收入为w元，
由题意得：，
∴当时，w有最大值，最大值为元，
∴当红布李的售价为元时，光明村农户一周的收入最大，最大收入是55125元；
（3）设本周光明村农户获得的收入为w元，
由题意得：，
，即，
，
，
，对称轴为直线，
∴当时，w有最大值，最大值为元，
∴本周光明村农户获得的最大收入和红布李售价分别为54000元和12元．
22．（1）；（2）直线与相切，证明见解析；（3）
【分析】（1）根据旋转变换的性质得到，，，根据等腰三角形的性质求出的大小即可；
（2）同（1）求出，根据切线的判定定理即可得到结论；
（3）如图所示，过点C作于E，过点B作交延长线与F，由旋转的性质可得，，，则，求出，，再求出，得到，则，即可得到。
【详解】解：（1）由旋转变换的性质可知，，，，
∴，
∴；
（2）直线与相切，证明如下
由旋转的性质可知，，，，
∴，
∴，
∴，
∵为的半径，
∴直线与相切；
（3）如图所示，过点C作于E，过点C作交延长线与F，
由旋转的性质可得，，，
∴，
∴，
∴，
∵，
∴，
∴，
∴，
∴。
【点睛】本题考查的是直线与圆的位置关系、旋转变换的性质、等边对等角，含30度角的直角三角形的性质，勾股定理的应用，掌握切线的判定定理、旋转变换的性质是解题的关键．