
还剩24页未读,
继续阅读
成套系列资料,整套一键下载
- (人教A版2019必修第一册)高一数学《考点•题型 •技巧》精讲与精练高分突破 第五章 三角函数同步单元必刷卷(基础卷)(考试版) 试卷 0 次下载
- (人教A版2019必修第一册)高一数学《考点•题型 •技巧》精讲与精练高分突破 专题强化二 不等式中的含参问题与恒成立问题【附答案解析】 试卷 0 次下载
- (人教A版2019必修第一册)高一数学《考点•题型 •技巧》精讲与精练高分突破 高一数学期末考试复习高分突破必刷检测卷(培优版)(全解全析) 试卷 0 次下载
- (人教A版2019必修第一册)高一数学《考点•题型 •技巧》精讲与精练高分突破 高一数学期末考试复习高分突破必刷检测卷(培优版)(考试版) 试卷 0 次下载
- (人教A版2019必修第一册)高一数学《考点•题型 •技巧》精讲与精练高分突破 高一数学期末考试复习高分突破必刷检测卷(基础版)(全解全析) 试卷 0 次下载
(人教A版2019必修第一册)高一数学《考点•题型 •技巧》精讲与精练高分突破 专题强化训练三 三角函数图像和最值的各类问题基础过关必刷30道【附答案解析】
展开
这是一份(人教A版2019必修第一册)高一数学《考点•题型 •技巧》精讲与精练高分突破 专题强化训练三 三角函数图像和最值的各类问题基础过关必刷30道【附答案解析】,共27页。
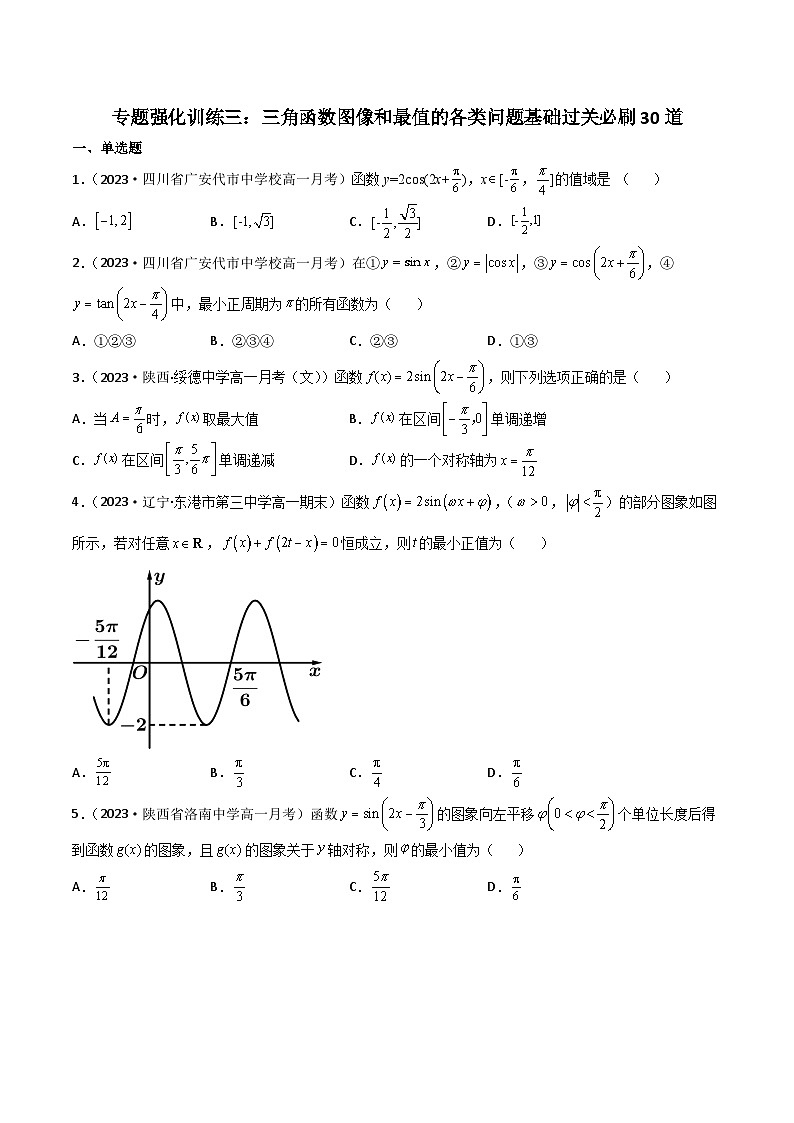
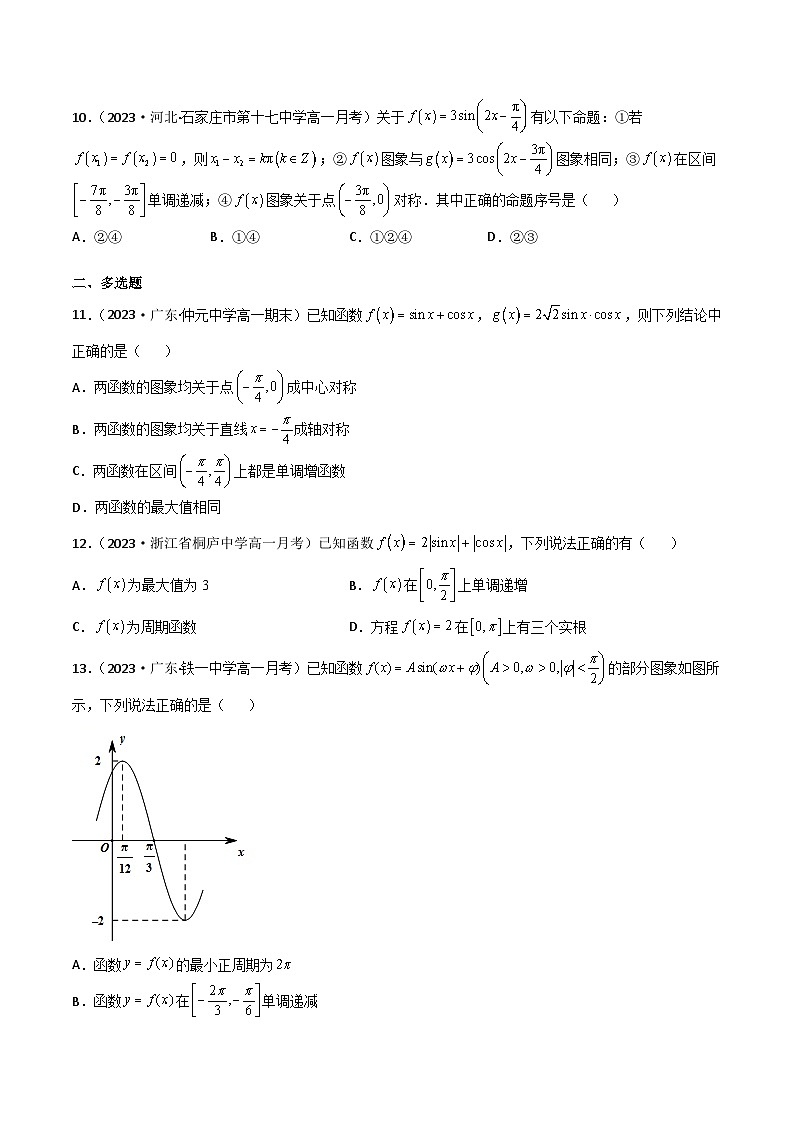
专题强化训练三:三角函数图像和最值的各类问题基础过关必刷30道一、单选题1.(2023·四川省广安代市中学校高一月考)函数y=2cos(2x+),x[-,]的值域是 ( )A. B. C. D.2.(2023·四川省广安代市中学校高一月考)在①,②,③,④中,最小正周期为的所有函数为( )A.①②③ B.②③④ C.②③ D.①③3.(2023·陕西·绥德中学高一月考(文))函数,则下列选项正确的是( )A.当时,取最大值 B.在区间单调递增C.在区间单调递减 D.的一个对称轴为4.(2023·辽宁·东港市第三中学高一期末)函数,(,)的部分图象如图所示,若对任意,恒成立,则的最小正值为( )A. B. C. D.5.(2023·陕西省洛南中学高一月考)函数的图象向左平移个单位长度后得到函数的图象,且的图象关于轴对称,则的最小值为( )A. B. C. D.6.(2023·安徽宿州·高一期中)已知函数,函数的图象可以由函数的图象先向右平移个单位长度,再将所得函数图象保持纵坐标不变,横坐标变为原来的得到.若方程在上恰有6个根,则的取值范围是( )A. B. C. D.7.(2023·全国·高一课时练习)已知函数的图象的一条对称轴与其相邻的一个对称中心的距离为,将的图象向右平移个单位长度得到函数的图象.若函数的图象在区间上是增函数,则的取值范围为( )A. B. C. D.8.(2023·湖南省岳阳县第一中学高一期末)已知函数,则下列结论正确的是( )A.的图象关于点对称B.在上的值域为C.若,则,D.将的图象向右平移个单位得的图象9.(2023·云南·昆明二十三中高一期中)若函数(,,)在一个周期内的图象如图所示,则( )A.B.的图象的一个对称中心为C.的单调递增区间是,D.把的图象上所有点的横坐标变为原来的,纵坐标不变,可得的图象10.(2023·河北·石家庄市第十七中学高一月考)关于有以下命题:①若,则;②图象与图象相同;③在区间单调递减;④图象关于点对称.其中正确的命题序号是( )A.②④ B.①④ C.①②④ D.②③二、多选题11.(2023·广东·仲元中学高一期末)已知函数,,则下列结论中正确的是( )A.两函数的图象均关于点成中心对称B.两函数的图象均关于直线成轴对称C.两函数在区间上都是单调增函数D.两函数的最大值相同12.(2023·浙江省桐庐中学高一月考)已知函数,下列说法正确的有( )A.为最大值为3 B.在上单调递增C.为周期函数 D.方程在上有三个实根13.(2023·广东·铁一中学高一月考)已知函数的部分图象如图所示,下列说法正确的是( )A.函数的最小正周期为B.函数在单调递减C.函数的图象关于直线对称D.该图象向右平移个单位可得的图象14.(2023·全国·高一课时练习)已知函数,则下列选项正确的是( )A.函数的最小正周期是B.函数在区间上单调递增C.函数的图象关于点对称D.函数的图象关于对称15.(2023·全国·高一单元测试)已知函数(其中)的图象关于点成中心对称,且与点相邻的一个最低点为,则下列判断正确的是( )A.函数中B.直线是函数图象的一条对称轴C.点是函数的一个对称中心D.函数与的图象的所有交点的横坐标之和为16.(2023·河北·正定中学高一月考)有以下四个命题,正确命题是( )A.函数的一个增区间是B.若函数为奇函数,则为的整数倍C.对于函数,若,则必是的整数倍D.函数的图像关于点对称17.(2023·云南省玉溪第一中学高一月考)设、是函数(,)的图象与直线的交点,若、两点距离的最小值为,是该函数图象上的一个点,则下列说法正确的是( )A.B.该函数图象的对称轴方程是,C.该函数图象的一个对称中心是D.在上单调递增三、填空题18.(2023·全国·高一课时练习)已知,,且在区间上有最小值,无最大值,则______.19.(2023·全国·高一课时练习)已知函数和的图象完全相同,若,则的取值范围是______.20.(2023·河北·张家口市第一中学高一月考)已知,函数,若恒成立,则m的取值范围是________.21.(2023·河北·张家口市第一中学高一期中)已知关于的方程在上有两个不同的实数根,则的取值范围是___________.四、解答题22.(2023·广东揭西·高一期末)已知函数.(Ⅰ)求的最小正周期; (Ⅱ)若在区间上的最大值为,求的最小值.23.(2023·福建·莆田第十五中学高一期末)已知函数,.(Ⅰ)求的最小正周期;(Ⅱ)求在上的最小值和最大值.24.(2019·广西·南宁三十六中高一月考)已知函数的部分图象如图所示:(I)求的解析式及对称中心坐标;(Ⅱ)将的图象向右平移个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数的图象,求函数在上的单调区间及最值.25.(2020·新疆·乌市八中高一月考)如图是函数的部分图象.(1)求函数的表达式;(2)若函数满足方程,求在内的所有实数根之和;(3)把函数的图象的周期扩大为原来的两倍,然后向右平移个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数的图象.若对任意的,方程在区间上至多有一个解,求正数的取值范围.26.(2023·湖南·益阳市箴言中学高一月考)设函数,其中.已知.(Ⅰ)求;(Ⅱ)将函数的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数的图象,求在上的最小值.27.(2023·全国·高一课时练习)函数(其中 ,,)的部分图象如图所示,先把函数 的图象上的各点的横坐标缩短为原来的(纵坐标不变),把得到的曲线向左平移个单位长度,再向上平移1个单位,得到函数的图象.(1)求函数图象的对称中心.(2)当时,求 的值域.(3)当时,方程 有解,求实数m的取值范围.28.(2023·河南洛阳·高一月考)已知函数.(1)若将函数图象上所有点的横坐标缩短到原来的倍(纵坐标不变),再将向左平移个单位,得到函数图象,求函数的解析式;(2)设,则是否存在实数,满足对于任意,都存在,使得成立?29.(2020·重庆·西南大学附中高一期末)已知函数,.(1)若图像纵坐标不变,横坐标变为原来的2倍,再向右平移个单位,得到的图像在 上单调递增,求的最大值;(2)若函数在内恰有两个零点,求的取值范围.30.(2023·江西省会昌中学高一月考(理))已知函数为奇函数,且图象的相邻两对称轴间的距离为.(1)当时,求的单调递减区间;(2)将函数的图象向右平移个单位长度,再把横坐标缩小为原来的 (纵坐标变),得到函数的图象,当时,求函数的值域.(3)(*)对于第(2)问中的函数,记方程在上的根从小到依次为,,,试确定的值,并求的值. 参考答案1.A【详解】令,因为x[-,],所以,而函数在上单调递增,在上单调递减,所以,,即函数的值域是.故选:A.2.C【详解】最小正周期为的所有函数为②③,函数的最小正周期为,函数的最小正周期为.故选:C.3.C【详解】因为函数,A.当时,,故A错误;B.因为,则,所以在区间不单调,故B错误;C. 因为,则,所以在区间单调递减,故C正确;D.因为 ,故D错误;故选:C4.B【详解】由图可知,,,由于,所以令,.所以.令,由于对任意,恒成立,所以,所以当时,取得最小正值为.故选:B5.C【详解】由题可得,的图象关于轴对称,,解得,,, 则的最小值为.故选:C.6.A【详解】由题意,由,得,,,中正数依次为,,,,,,,…,在上恰有6个根,则,解得.故选:A.7.B【详解】由题意,知,∴,∴,∴,∴,由,得,即的增区间为,∴,∴,,∴.∵,∴,故选:B.8.D【详解】,对于A:令,可得,所以点不是的图象的对称中心,故选项A不正确;对于B:当时,,,所以,故选项B不正确;对于C:的最小正周期为,所以若,则,,故选项C不正确;对于D:将的图象向右平移个单位得的图象,故选项D正确;故选:D.9.B【详解】由题图可知,函数的最小正周期,故,解得,所以,又函数的图象经过点,所以,即,因为,所以,所以,解得,所以,故A不正确;因为,所以的图象的一个对称中心为,故B正确;令,,解得,,所以的单调递增区间是,,故C错误;把的图象上所有点的横坐标变为原来的,纵坐标不变,可得到的图象,故D错误.故选:B.10.A【详解】,,所以①错误;,所以②正确;,,正弦函数在不单调,所以③错误;,图象关于点对称,所以④正确.故选:A11.CD【详解】根据题意得,,.对于选项AB,因,,所以函数的图象关于点成中心对称,而函数的图象关于直线成轴对称,故AB都错;对于选项C,当时,,,因在上单调递增,所以两函数在区间上都是单调增函数,故C正确;对于选项D,因,,所以,故D正确.故选:CD.12.CD【详解】对于A选项,由平方关系知时,,时,,所以,所以,A选项错误;对于B选项,,,则,故函数在上不是增函数,B选项错误;对于C选项,,故函数为周期函数,C选项正确;对于D选项,由,解得或或,所以,方程在上有三个实根,D选项正确.故选:CD.13.CD【详解】由图象可知:A=2,周期;由,解得:,故函数.对于A:,故A错误;对于B:当 时,因为上正弦函数先减后增,不单调,所以在上不单调,故B错误;对于C:当 时,即直线是的一条对称轴,故C正确;对于D:向右平移个单位得到,故D正确.故选:CD.14.AD【详解】 ,因为,函数的最小正周期是,选项A正确;由,得,所以区间不是函数的单调递增区间,选项B错误;由,得,所以点不是函数的对称中心,选项C错误;由,得,当时,,所以是函数的对称轴,选项D正确.故选:AD.15.ACD解:函数(其中,,的图象关于点成中心对称,且与点相邻的一个最低点为,则,,进一步解得,,故A正确.由于函数(其中,,的图象关于点成中心对称,,解得,由于,当时,..对于B:当时,,故B不正确;对于C:由,,解得,,当时,对称中心为:,故C正确;对于D:由于:,则:,函数的图象与有6个交点.根据函数的交点设横坐标从左到右分别为、、、、、,由,,解得,,所以,,,所以所以函数的图象的所有交点的横坐标之和为,故D正确.正确的判断是ACD.故选:ACD.16.ABD【详解】对选项A,,因为,,所以在为减函数,即在为增函数,故A正确.对选项B,为奇函数,则,,即为的整数倍,故B正确.对选项C,因为在定义域范围内为增函数,且周期为,所以若,则必是的整数倍,故C错误.对选项D,,则,所以的图像关于点对称,故D正确.故选:ABD17.ABC、是函数(,)的图象与直线的交点,且、两点距离的最小值为6,则函数的最小正周期为,,所以,将点P的坐标代入函数的解析式,可得,则,,,则,,,对于A选项,显然正确;对于B选项,由(),解得(),所以函数图象的对称轴方程是,,显然正确;对于C选项,,显然正确;对于D选项,当时,,所以函数在区间上不单调,显然错误.故选:ABC.18.依题意,当时,y有最小值,即,则,所以.因为在区间上有最小值,无最大值,所以,即,令,得.故答案为:19.解:因为,所以,则.因为,所以,所以,所以.故答案为:.20..【详解】由题意,函数,因为,所以,所以,因为恒成立,所以,解得,所以实数的取值范围是.故答案为:.21.【详解】 , ,即, ,即,,,设,则在上有两个不同的实数根, ,,的图像有两个不同的交点,如图由图象可知, ,即 故答案为:22.(Ⅰ) ;(Ⅱ).【详解】(Ⅰ),所以的最小正周期为.(Ⅱ)由(Ⅰ)知.因为,所以.要使得在上的最大值为,即在上的最大值为1.所以,即.所以的最小值为.23.(Ⅰ);(Ⅱ)最小值和最大值.【详解】由已知,有的最小正周期.(2)∵在区间上是减函数,在区间上是增函数,,,∴函数在闭区间上的最大值为,最小值为.考点:1.两角和与差的正弦公式、二倍角的正弦与余弦公式;2.三角函数的周期性和单调性.24.解:(I)由图像可知:,可得:又由于,可得:,所以由图像知,,又因为所以,.所以 令(),得:()所以的对称中心的坐标为() (II)由已知的图像变换过程可得: 由的图像知函数在上的单调增区间为,单调减区间 当时,取得最大值2;当时,取得最小值.25.解:(Ⅰ)由图可知:,即,又由图可知:是五点作图法中的第二点,,即. (Ⅱ)因为的周期为,在内恰有个周期.⑴当时,方程在内有个实根,设为,结合图像知 ,故所有实数根之和为 ; ⑵当时,方程在内有个实根为,故所有实数根之和为 ; ⑶当时,方程在内有个实根,设为,结合图像知 ,故所有实数根之和为 ; 综上:当时,方程所有实数根之和为 ;当时,方程所有实数根之和为 ; (Ⅲ),函数的图象如图所示:则当图象伸长为原来的倍以上时符合题意,所以.26.解:(Ⅰ)因为,所以由题设知,所以,.故,,又,所以.(Ⅱ)由(Ⅰ)得所以.因为,所以,当,即时,取得最小值.27.(1)根据图象可知,,∴,∴, ,将代入得, ,即,解得 ,,∵,∴, ,∴.函数的图象上的各点的横坐标缩短为原来的(纵坐标不变),可得 ,曲线再向左平移个单位长度,再向上平移1个单位得令,解得 ∴此函数图象的对称中心为.(2)当时, ,,即 的值域为.(3),令,由(2)知, ,因此m的取值范围为.28.【详解】(1)将函数图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到,再向左平移个单位,得到函数所以函数的解析式为:(2),即;又,,即假设存在实数,满足对任意,都存在,使得成立,则的值域是值域的子集,即则,此方程组无解,故满足题意得实数不存在.29【详解】(1)由题变换后图像的解析式是:,,,,,,由题:,且,,即的最大值为;(2),设,当时,.它的图形如图所示:则.令,,①当时,,此时,仅有一个零点,对应一个x,不符题意;②当时,,此时,仅有一个零点,对应两个x,符合题意;③当时,,此时,有两个零点,,由图,各对应一个x,符合题意;④当时,若有两根,则必有,与矛盾;⑤当时,若取有两相等实根,则,白①②可知,;⑥当在上有一根,在或上有一根;或,则或,解得:,综上,.30.【详解】(1)由题意,函数因为函数图象的相邻两对称轴间的距离为,所以,可得,又由函数为奇函数,可得,所以,因为,所以,所以函数,令,解得,可函数的递减区间为,再结合,可得函数的减区间为.(2)将函数的图象向右平移个单位长度,可得的图象,再把横坐标缩小为原来的,得到函数的图象,当时,,当时,函数取得最小值,最小值为,当时,函数取得最大值,最小值为,故函数的值域.(3)由方程,即,即,因为,可得,设,其中,即,结合正弦函数的图象,可得方程在区间有5个解,即,其中,即解得所以.
专题强化训练三:三角函数图像和最值的各类问题基础过关必刷30道一、单选题1.(2023·四川省广安代市中学校高一月考)函数y=2cos(2x+),x[-,]的值域是 ( )A. B. C. D.2.(2023·四川省广安代市中学校高一月考)在①,②,③,④中,最小正周期为的所有函数为( )A.①②③ B.②③④ C.②③ D.①③3.(2023·陕西·绥德中学高一月考(文))函数,则下列选项正确的是( )A.当时,取最大值 B.在区间单调递增C.在区间单调递减 D.的一个对称轴为4.(2023·辽宁·东港市第三中学高一期末)函数,(,)的部分图象如图所示,若对任意,恒成立,则的最小正值为( )A. B. C. D.5.(2023·陕西省洛南中学高一月考)函数的图象向左平移个单位长度后得到函数的图象,且的图象关于轴对称,则的最小值为( )A. B. C. D.6.(2023·安徽宿州·高一期中)已知函数,函数的图象可以由函数的图象先向右平移个单位长度,再将所得函数图象保持纵坐标不变,横坐标变为原来的得到.若方程在上恰有6个根,则的取值范围是( )A. B. C. D.7.(2023·全国·高一课时练习)已知函数的图象的一条对称轴与其相邻的一个对称中心的距离为,将的图象向右平移个单位长度得到函数的图象.若函数的图象在区间上是增函数,则的取值范围为( )A. B. C. D.8.(2023·湖南省岳阳县第一中学高一期末)已知函数,则下列结论正确的是( )A.的图象关于点对称B.在上的值域为C.若,则,D.将的图象向右平移个单位得的图象9.(2023·云南·昆明二十三中高一期中)若函数(,,)在一个周期内的图象如图所示,则( )A.B.的图象的一个对称中心为C.的单调递增区间是,D.把的图象上所有点的横坐标变为原来的,纵坐标不变,可得的图象10.(2023·河北·石家庄市第十七中学高一月考)关于有以下命题:①若,则;②图象与图象相同;③在区间单调递减;④图象关于点对称.其中正确的命题序号是( )A.②④ B.①④ C.①②④ D.②③二、多选题11.(2023·广东·仲元中学高一期末)已知函数,,则下列结论中正确的是( )A.两函数的图象均关于点成中心对称B.两函数的图象均关于直线成轴对称C.两函数在区间上都是单调增函数D.两函数的最大值相同12.(2023·浙江省桐庐中学高一月考)已知函数,下列说法正确的有( )A.为最大值为3 B.在上单调递增C.为周期函数 D.方程在上有三个实根13.(2023·广东·铁一中学高一月考)已知函数的部分图象如图所示,下列说法正确的是( )A.函数的最小正周期为B.函数在单调递减C.函数的图象关于直线对称D.该图象向右平移个单位可得的图象14.(2023·全国·高一课时练习)已知函数,则下列选项正确的是( )A.函数的最小正周期是B.函数在区间上单调递增C.函数的图象关于点对称D.函数的图象关于对称15.(2023·全国·高一单元测试)已知函数(其中)的图象关于点成中心对称,且与点相邻的一个最低点为,则下列判断正确的是( )A.函数中B.直线是函数图象的一条对称轴C.点是函数的一个对称中心D.函数与的图象的所有交点的横坐标之和为16.(2023·河北·正定中学高一月考)有以下四个命题,正确命题是( )A.函数的一个增区间是B.若函数为奇函数,则为的整数倍C.对于函数,若,则必是的整数倍D.函数的图像关于点对称17.(2023·云南省玉溪第一中学高一月考)设、是函数(,)的图象与直线的交点,若、两点距离的最小值为,是该函数图象上的一个点,则下列说法正确的是( )A.B.该函数图象的对称轴方程是,C.该函数图象的一个对称中心是D.在上单调递增三、填空题18.(2023·全国·高一课时练习)已知,,且在区间上有最小值,无最大值,则______.19.(2023·全国·高一课时练习)已知函数和的图象完全相同,若,则的取值范围是______.20.(2023·河北·张家口市第一中学高一月考)已知,函数,若恒成立,则m的取值范围是________.21.(2023·河北·张家口市第一中学高一期中)已知关于的方程在上有两个不同的实数根,则的取值范围是___________.四、解答题22.(2023·广东揭西·高一期末)已知函数.(Ⅰ)求的最小正周期; (Ⅱ)若在区间上的最大值为,求的最小值.23.(2023·福建·莆田第十五中学高一期末)已知函数,.(Ⅰ)求的最小正周期;(Ⅱ)求在上的最小值和最大值.24.(2019·广西·南宁三十六中高一月考)已知函数的部分图象如图所示:(I)求的解析式及对称中心坐标;(Ⅱ)将的图象向右平移个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数的图象,求函数在上的单调区间及最值.25.(2020·新疆·乌市八中高一月考)如图是函数的部分图象.(1)求函数的表达式;(2)若函数满足方程,求在内的所有实数根之和;(3)把函数的图象的周期扩大为原来的两倍,然后向右平移个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数的图象.若对任意的,方程在区间上至多有一个解,求正数的取值范围.26.(2023·湖南·益阳市箴言中学高一月考)设函数,其中.已知.(Ⅰ)求;(Ⅱ)将函数的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移个单位,得到函数的图象,求在上的最小值.27.(2023·全国·高一课时练习)函数(其中 ,,)的部分图象如图所示,先把函数 的图象上的各点的横坐标缩短为原来的(纵坐标不变),把得到的曲线向左平移个单位长度,再向上平移1个单位,得到函数的图象.(1)求函数图象的对称中心.(2)当时,求 的值域.(3)当时,方程 有解,求实数m的取值范围.28.(2023·河南洛阳·高一月考)已知函数.(1)若将函数图象上所有点的横坐标缩短到原来的倍(纵坐标不变),再将向左平移个单位,得到函数图象,求函数的解析式;(2)设,则是否存在实数,满足对于任意,都存在,使得成立?29.(2020·重庆·西南大学附中高一期末)已知函数,.(1)若图像纵坐标不变,横坐标变为原来的2倍,再向右平移个单位,得到的图像在 上单调递增,求的最大值;(2)若函数在内恰有两个零点,求的取值范围.30.(2023·江西省会昌中学高一月考(理))已知函数为奇函数,且图象的相邻两对称轴间的距离为.(1)当时,求的单调递减区间;(2)将函数的图象向右平移个单位长度,再把横坐标缩小为原来的 (纵坐标变),得到函数的图象,当时,求函数的值域.(3)(*)对于第(2)问中的函数,记方程在上的根从小到依次为,,,试确定的值,并求的值. 参考答案1.A【详解】令,因为x[-,],所以,而函数在上单调递增,在上单调递减,所以,,即函数的值域是.故选:A.2.C【详解】最小正周期为的所有函数为②③,函数的最小正周期为,函数的最小正周期为.故选:C.3.C【详解】因为函数,A.当时,,故A错误;B.因为,则,所以在区间不单调,故B错误;C. 因为,则,所以在区间单调递减,故C正确;D.因为 ,故D错误;故选:C4.B【详解】由图可知,,,由于,所以令,.所以.令,由于对任意,恒成立,所以,所以当时,取得最小正值为.故选:B5.C【详解】由题可得,的图象关于轴对称,,解得,,, 则的最小值为.故选:C.6.A【详解】由题意,由,得,,,中正数依次为,,,,,,,…,在上恰有6个根,则,解得.故选:A.7.B【详解】由题意,知,∴,∴,∴,∴,由,得,即的增区间为,∴,∴,,∴.∵,∴,故选:B.8.D【详解】,对于A:令,可得,所以点不是的图象的对称中心,故选项A不正确;对于B:当时,,,所以,故选项B不正确;对于C:的最小正周期为,所以若,则,,故选项C不正确;对于D:将的图象向右平移个单位得的图象,故选项D正确;故选:D.9.B【详解】由题图可知,函数的最小正周期,故,解得,所以,又函数的图象经过点,所以,即,因为,所以,所以,解得,所以,故A不正确;因为,所以的图象的一个对称中心为,故B正确;令,,解得,,所以的单调递增区间是,,故C错误;把的图象上所有点的横坐标变为原来的,纵坐标不变,可得到的图象,故D错误.故选:B.10.A【详解】,,所以①错误;,所以②正确;,,正弦函数在不单调,所以③错误;,图象关于点对称,所以④正确.故选:A11.CD【详解】根据题意得,,.对于选项AB,因,,所以函数的图象关于点成中心对称,而函数的图象关于直线成轴对称,故AB都错;对于选项C,当时,,,因在上单调递增,所以两函数在区间上都是单调增函数,故C正确;对于选项D,因,,所以,故D正确.故选:CD.12.CD【详解】对于A选项,由平方关系知时,,时,,所以,所以,A选项错误;对于B选项,,,则,故函数在上不是增函数,B选项错误;对于C选项,,故函数为周期函数,C选项正确;对于D选项,由,解得或或,所以,方程在上有三个实根,D选项正确.故选:CD.13.CD【详解】由图象可知:A=2,周期;由,解得:,故函数.对于A:,故A错误;对于B:当 时,因为上正弦函数先减后增,不单调,所以在上不单调,故B错误;对于C:当 时,即直线是的一条对称轴,故C正确;对于D:向右平移个单位得到,故D正确.故选:CD.14.AD【详解】 ,因为,函数的最小正周期是,选项A正确;由,得,所以区间不是函数的单调递增区间,选项B错误;由,得,所以点不是函数的对称中心,选项C错误;由,得,当时,,所以是函数的对称轴,选项D正确.故选:AD.15.ACD解:函数(其中,,的图象关于点成中心对称,且与点相邻的一个最低点为,则,,进一步解得,,故A正确.由于函数(其中,,的图象关于点成中心对称,,解得,由于,当时,..对于B:当时,,故B不正确;对于C:由,,解得,,当时,对称中心为:,故C正确;对于D:由于:,则:,函数的图象与有6个交点.根据函数的交点设横坐标从左到右分别为、、、、、,由,,解得,,所以,,,所以所以函数的图象的所有交点的横坐标之和为,故D正确.正确的判断是ACD.故选:ACD.16.ABD【详解】对选项A,,因为,,所以在为减函数,即在为增函数,故A正确.对选项B,为奇函数,则,,即为的整数倍,故B正确.对选项C,因为在定义域范围内为增函数,且周期为,所以若,则必是的整数倍,故C错误.对选项D,,则,所以的图像关于点对称,故D正确.故选:ABD17.ABC、是函数(,)的图象与直线的交点,且、两点距离的最小值为6,则函数的最小正周期为,,所以,将点P的坐标代入函数的解析式,可得,则,,,则,,,对于A选项,显然正确;对于B选项,由(),解得(),所以函数图象的对称轴方程是,,显然正确;对于C选项,,显然正确;对于D选项,当时,,所以函数在区间上不单调,显然错误.故选:ABC.18.依题意,当时,y有最小值,即,则,所以.因为在区间上有最小值,无最大值,所以,即,令,得.故答案为:19.解:因为,所以,则.因为,所以,所以,所以.故答案为:.20..【详解】由题意,函数,因为,所以,所以,因为恒成立,所以,解得,所以实数的取值范围是.故答案为:.21.【详解】 , ,即, ,即,,,设,则在上有两个不同的实数根, ,,的图像有两个不同的交点,如图由图象可知, ,即 故答案为:22.(Ⅰ) ;(Ⅱ).【详解】(Ⅰ),所以的最小正周期为.(Ⅱ)由(Ⅰ)知.因为,所以.要使得在上的最大值为,即在上的最大值为1.所以,即.所以的最小值为.23.(Ⅰ);(Ⅱ)最小值和最大值.【详解】由已知,有的最小正周期.(2)∵在区间上是减函数,在区间上是增函数,,,∴函数在闭区间上的最大值为,最小值为.考点:1.两角和与差的正弦公式、二倍角的正弦与余弦公式;2.三角函数的周期性和单调性.24.解:(I)由图像可知:,可得:又由于,可得:,所以由图像知,,又因为所以,.所以 令(),得:()所以的对称中心的坐标为() (II)由已知的图像变换过程可得: 由的图像知函数在上的单调增区间为,单调减区间 当时,取得最大值2;当时,取得最小值.25.解:(Ⅰ)由图可知:,即,又由图可知:是五点作图法中的第二点,,即. (Ⅱ)因为的周期为,在内恰有个周期.⑴当时,方程在内有个实根,设为,结合图像知 ,故所有实数根之和为 ; ⑵当时,方程在内有个实根为,故所有实数根之和为 ; ⑶当时,方程在内有个实根,设为,结合图像知 ,故所有实数根之和为 ; 综上:当时,方程所有实数根之和为 ;当时,方程所有实数根之和为 ; (Ⅲ),函数的图象如图所示:则当图象伸长为原来的倍以上时符合题意,所以.26.解:(Ⅰ)因为,所以由题设知,所以,.故,,又,所以.(Ⅱ)由(Ⅰ)得所以.因为,所以,当,即时,取得最小值.27.(1)根据图象可知,,∴,∴, ,将代入得, ,即,解得 ,,∵,∴, ,∴.函数的图象上的各点的横坐标缩短为原来的(纵坐标不变),可得 ,曲线再向左平移个单位长度,再向上平移1个单位得令,解得 ∴此函数图象的对称中心为.(2)当时, ,,即 的值域为.(3),令,由(2)知, ,因此m的取值范围为.28.【详解】(1)将函数图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到,再向左平移个单位,得到函数所以函数的解析式为:(2),即;又,,即假设存在实数,满足对任意,都存在,使得成立,则的值域是值域的子集,即则,此方程组无解,故满足题意得实数不存在.29【详解】(1)由题变换后图像的解析式是:,,,,,,由题:,且,,即的最大值为;(2),设,当时,.它的图形如图所示:则.令,,①当时,,此时,仅有一个零点,对应一个x,不符题意;②当时,,此时,仅有一个零点,对应两个x,符合题意;③当时,,此时,有两个零点,,由图,各对应一个x,符合题意;④当时,若有两根,则必有,与矛盾;⑤当时,若取有两相等实根,则,白①②可知,;⑥当在上有一根,在或上有一根;或,则或,解得:,综上,.30.【详解】(1)由题意,函数因为函数图象的相邻两对称轴间的距离为,所以,可得,又由函数为奇函数,可得,所以,因为,所以,所以函数,令,解得,可函数的递减区间为,再结合,可得函数的减区间为.(2)将函数的图象向右平移个单位长度,可得的图象,再把横坐标缩小为原来的,得到函数的图象,当时,,当时,函数取得最小值,最小值为,当时,函数取得最大值,最小值为,故函数的值域.(3)由方程,即,即,因为,可得,设,其中,即,结合正弦函数的图象,可得方程在区间有5个解,即,其中,即解得所以.
相关资料
更多









