人教版九年级下册第二十七章 相似27.2 相似三角形27.2.3 相似三角形应用举例教学演示课件ppt

这是一份人教版九年级下册第二十七章 相似27.2 相似三角形27.2.3 相似三角形应用举例教学演示课件ppt，共21页。PPT课件主要包含了新课导入，测量金字塔高度，知识点1，推进新课，x54m，测量河的宽度，知识点2，基础巩固，解∵EB∥DC，随堂演练等内容，欢迎下载使用。

胡夫金字塔是埃及现存规模最大的金字塔，被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向，塔基呈正方形，每边长约230多米。据考证，为建成大金字塔，共动用了10万人花了20年时间。原高146.59米，但由于经过几千年的风吹雨打，顶端被风化侵蚀，所以高度有所降低。
利用学过的相似三角形的知识，如何来测量金字塔的高度呢？
例4 据传说，古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度。
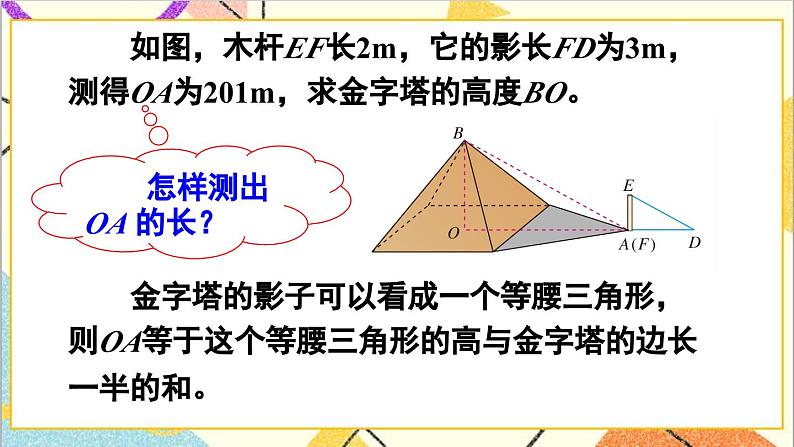
如图，木杆EF长2m，它的影长FD为3m，测得OA为201m，求金字塔的高度BO。
　　怎样测出OA 的长？
金字塔的影子可以看成一个等腰三角形，则OA等于这个等腰三角形的高与金字塔的边长一半的和。
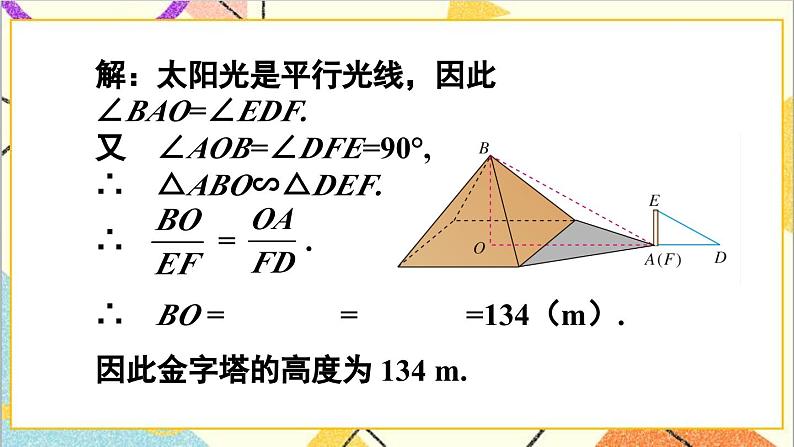
　　解：太阳光是平行光线，因此　　∠BAO=∠EDF.　　又　∠AOB=∠DFE=90°,　　∴　△ABO∽△DEF.　　∴　　　=　　 .　　∴　BO =　　　 =　　　 =134（m）.　　因此金字塔的高度为 134 m.
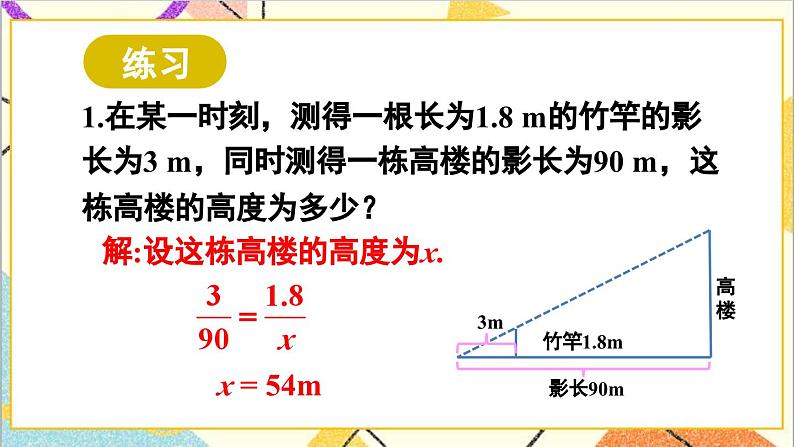
1.在某一时刻，测得一根长为1.8 m的竹竿的影长为3 m，同时测得一栋高楼的影长为90 m，这栋高楼的高度为多少？
解:设这栋高楼的高度为x.
在无法过河的条件下，怎样估算河的宽度？
　　例5　如图，为了估算河的宽度，我们可以在河对岸选定一个目标点 P，在近岸取点 Q 和 S，使点 P，Q，S 共线且直线 PS 与河垂直，接着在过点 S 且与 PS 垂直的直线 a 上选择适当的点 T，确定 PT 与过点 Q 且垂直 PS 的直线 b 的交点 R。已测得 QS = 45 m，ST = 90 m，QR = 60 m，请根据这些数据，计算河宽 PQ。
　　解：∵ ∠PQR=∠PST=90°，∠P=∠P，　　∴　△PQR∽△PST. ∴　　即　　　　　 ， ,　　　　PQ×90=（PQ+45）×60. 　　解得　PQ=90（m）.　　因此，河宽大约为 90 m.
1.如图，测得BD=120 m，DC=60 m，EC=50 m，求河宽AB。
解：∵∠ABD=∠ECD=90°，∠ADB=∠EDC,∴△ABD∽△ECD.
即 . 解得AB=100（m）
2.为了测量被池塘隔开的A，B两点之间的距离，根据实际情况，作出如右图形，其中AB⊥BE，EF⊥BE，AF交BE于D，C在BD上。有四位同学分别测量出以下四组数据：①BC，AC； ②EF，DE，BD；③DE，DC，BC ；④DC,DB,AC 。能根据所测数据求出A，B间距离的有（ ）
A.1组B.2组C.3组D.0组
1.如图，利用标杆BE测量建筑物的高度.如果标杆BE高1.2 m，测得AB=1.6 m，BC=8.4 m，则楼高CD是多少？
∴△AEB∽△ADC.
∴ ，
求得 DC=7.5（m）.
2.为了测量一池塘的宽AB，在岸边找到了一点C，使AC⊥AB，在AC上找到一点D，在BC上找到一点E，使DE⊥AC，测出AD=35 m，DC=35 m，DE=30 m，求池塘的宽AB。
解：∵AC⊥AB，DE⊥AC，
∴AB∥DE, ∴△CDE∽△CAB,
求得 AB=60（m）.
3.如图，为了测量一栋大楼的高度，王青同学在她脚下放了一面镜子，然后向后退，直至她刚好在镜子中看到大楼顶部，这时∠LMK等于∠SMT吗？如果王青身高1.55 m，她估计自己的眼睛离地面1.50 m，同时量得LM＝30 cm，MS＝2 m，这栋大楼有多高？
解：∠LMK=∠SMT。又∵∠KLM=∠TSM=90°,
∴△KLM∽△TSM,
即 ,
解得 TS=10(m).
∴这栋大楼有10 m高.
根据题意建立相似三角形模型
如图，点D、E分别在AC、BC上，如果测得CD=20 m，CE=40 m，AD=100 m，BE=20 m，DE=45 m，求A、B两地间的距离。
解：由题意可知，CD=20 m，CE=40 m，AD=100 m，BE=20 m，DE=45 m.
∴AC=AD+DC=120 m，BC=BE+CE=60 m
∴ ,而∠C=∠C,∴△CDE∽△CBA.
∴ ,∴AB=135(m).
∴A、B两地间的距离为135 m.
1.从课后习题中选取；2.完成练习册本课时的习题.