广东省佛山市南海实验中学2023-2024学年九上数学期末教学质量检测模拟试题含答案

这是一份广东省佛山市南海实验中学2023-2024学年九上数学期末教学质量检测模拟试题含答案，共8页。
学校_______ 年级_______ 姓名_______
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。
一、选择题（每题4分，共48分）
1．在一个不透明的布袋中装有9个白球和若干个黑球，它们除颜色不同外，其余均相同。若从中随机摸出一个球，摸到白球的概率是，则黑球的个数为（ ）
A．3B．12C．18D．27
2．在平面直角坐标系中，将抛物线向上平移1个单位后所得抛物线的解析式为（ ）
A．B．C．D．
3．sin45°的值是（ ）
A．B．C．D．
4．掷一枚质地均匀的硬币10次，下列说法正确的是（ ）
A．必有5次正面朝上B．可能有5次正面朝上
C．掷2次必有1次正面朝上D．不可能10次正面朝上
5．若一元二次方程x2﹣4x﹣4m＝0有两个不等的实数根，则反比例函数y＝的图象所在的象限是（ ）
A．第一、二象限B．第一、三象限
C．第二、四象限D．第三、四象限
6．主视图、左视图、俯视图分别为下列三个图形的物体是（ ）
A．B．C．D．
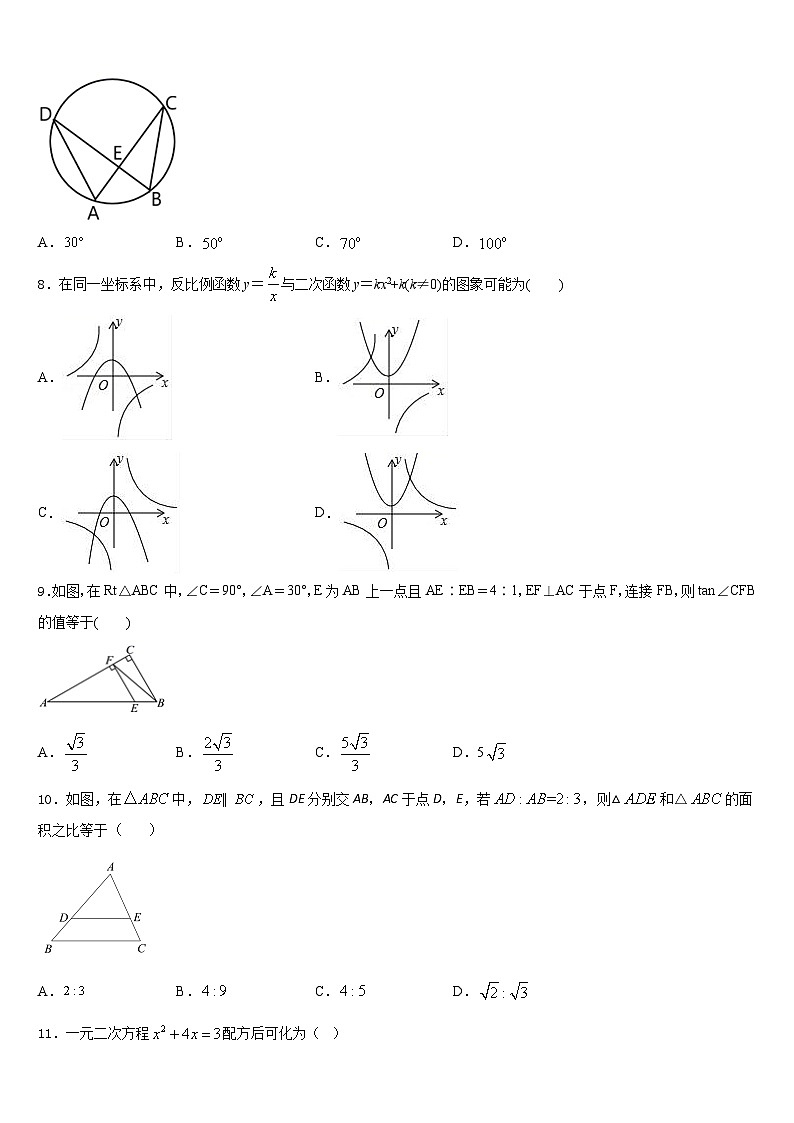
7．如图，中，弦相交于点，连接，若，，则（ ）
A．B．C．D．
8．在同一坐标系中，反比例函数y＝与二次函数y＝kx2+k(k≠0)的图象可能为( )
A．B．
C．D．
9．如图，在Rt△ABC中，∠C＝90°，∠A＝30°，E为AB上一点且AE∶EB＝4∶1，EF⊥AC于点F，连接FB，则tan∠CFB的值等于( )
A．B．C．D．5
10．如图，在中，，且DE分别交AB，AC于点D，E，若，则△和△的面积之比等于（ ）
A．B．C．D．
11．一元二次方程配方后可化为（ ）
A．B．C．D．
12．圆内接正三角形、正方形、正六边形的边长之比为( )
A．1：2：3B．1：：C．：：1D．无法确定
二、填空题（每题4分，共24分）
13．计算：________．
14．如图，在中，交于点，交于点．若、、，则的长为_________．
15．如图，将一个顶角为30°角的等腰△ABC绕点A顺时针旋转一个角度α（0＜α＜180°）得到△AB'C′，使得点B′、A、C在同一条直线上，则α等于_____°．
16．如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”，在△ABC中，AB=AC，若△ABC是“好玩三角形”，则tanB____________。
17．如图，、、、是上四个点，连接、，过作交圆周于点，连接，若，则的度数为___________．
18．如图，圆锥的母线长为5，底面圆直径CD与高AB相等，则圆锥的侧面积为_____．
三、解答题（共78分）
19．（8分）如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C
（1）求证：∠CBP=∠ADB
（2）若OA=2，AB=1，求线段BP的长.
20．（8分）如图，在平面直角坐标系xOy中，点A（3，3），点B（4，0），点C（0，﹣1）．
（1）以点C为中心，把△ABC逆时针旋转90°，请在图中画出旋转后的图形△A′B′C，点B′的坐标为________；
（2）在（1）的条件下，求出点A经过的路径的长（结果保留π）．
21．（8分）如图，在中，，，.将绕点逆时针方向旋转60°得到，连接，求线段的长．
22．（10分）如图，在中，，，点均在边上，且．
（1）将绕A点逆时针旋转，可使AB与AC重合，画出旋转后的图形，在原图中补出旋转后的图形．
（2）求和的度数．
23．（10分）已知：如图,在⊙O中,弦交于点,.
求证：.
24．（10分）《庄子·天下》：“一尺之棰，日取其半，万世不竭．”意思是说：一尺长的木棍，每天截掉一半，永远也截不完．我国智慧的古代人在两千多年前就有了数学极限思想，今天我们运用此数学思想研究下列问题．
（规律探索）
（1）如图1所示的是边长为1的正方形，将它剪掉一半，则S阴影1＝1－＝
如图2，在图1的基础上，将阴影部分再裁剪掉—半，则S阴影2＝1－－()2 ＝____；
同种操作，如图3，S阴影3＝1－－()2－()3 ＝__________；
如图4，S阴影4＝1－－()2－()3－()4 ＝___________；
……若同种地操作n次，则S阴影n＝1－－()2－()3－…－()n ＝_________．
于是归纳得到：+()2+()3+…+()n =_________．
（理论推导）
（2）阅读材料：求1+2+22+23+24+…+22015+22016的值．
解：设S=1+2+22+23+24+…+22015+22016，①
将①×2得：2S=2+22+23+24+…+22016+22017，②
由②-①得：2S—S=22017—1，即=22017-1．
即1+2+22+23+24+…+22015+22016＝22017-1
根据上述材料，试求出+()2+()3+…+()n 的表达式，写出推导过程．
（规律应用）
（3）比较＋＋＋…… __________1（填“”、“”或“=”）
25．（12分）如图，抛物线y＝ax2+bx+3（a≠0）的对称轴为直线x＝﹣1，抛物线交x轴于A、C两点，与直线y＝x﹣1交于A、B两点，直线AB与抛物线的对称轴交于点E．
（1）求抛物线的解析式．
（2）点P在直线AB上方的抛物线上运动，若△ABP的面积最大，求此时点P的坐标．
（3）在平面直角坐标系中，以点B、E、C、D为顶点的四边形是平行四边形，请直接写出符合条件点D的坐标．
26．（12分）如图，在矩形ABCD中，AB＝6，BC＝13，BE＝4，点F从点B出发，在折线段BA﹣AD上运动，连接EF，当EF⊥BC时停止运动，过点E作EG⊥EF，交矩形的边于点G，连接FG．设点F运动的路程为x，△EFG的面积为S．
（1）当点F与点A重合时，点G恰好到达点D，此时x＝ ，当EF⊥BC时，x＝ ；
（2）求S关于x的函数解析式，并直接写出自变量x的取值范围；
（3）当S＝15时，求此时x的值．
参考答案
一、选择题（每题4分，共48分）
1、C
2、B
3、B
4、B
5、B
6、A
7、C
8、D
9、C
10、B
11、B
12、C
二、填空题（每题4分，共24分）
13、
14、6
15、1°
16、1或
17、
18、5π
三、解答题（共78分）
19、（1）证明见解析；（2）BP=1.
20、（1）图见解析；B′的坐标为（﹣1，3）；（2）.
21、
22、（1）见解析；（2），.
23、证明见解析.
24、（1）；；；()n；1 - ()n ；（2）+()2+()3+…+()n = 1-()n，推导过程见解析；（3）=
25、 (1)y＝﹣x2﹣2x+3；(2)点P(，)；(3)符合条件的点D的坐标为D1(0，3)，D2(﹣6，﹣3)，D3(﹣2，﹣7)．
26、（1）6；10；（2）S＝x2+9x+12（0＜x≤6）；S＝x2﹣21x+102（6＜x≤10）；（3）﹣6+2．