福建省龙岩市长汀县2023-2024学年七年级上学期期末数学试题（含解析）

这是一份福建省龙岩市长汀县2023-2024学年七年级上学期期末数学试题（含解析），共16页。试卷主要包含了选择题，填空，解答题等内容，欢迎下载使用。

（考试时间：120分钟；满分150分）
一、选择题（每小题4分，共40分）
1．作家莫言获得诺贝尔文学奖之后，他的代表作品《蛙》的销售量比获奖之前增长了180倍，达到2100000册，将2100000用科学记数法表示为（ ）
A．B．C．D．
2．的绝对值是（ ）
A．B．C．D．3
3．下列各式正确的是（ ）
A．﹣8+5=3B．（﹣2）3=6C．﹣（a﹣b）=﹣a+bD．2（a+b）=2a+b
4．如图是一个正方体的展开图，把展开图折叠成小正方体后，和“建”字所在面相对的面上的字是（ ）
A．跟B．百C．走D．年
5．如图所示，有理数a、b在数轴上的位置如图，则下列说法错误的是（ ）
A．b﹣a＞0B．a+b＜0C．ab＜0D．b＜a
6．与的度数分别是和，且与都是的补角，那么与的关系是( )．
A．不互余且不相等B．不互余但相等
C．互为余角但不相等D．互为余角且相等
7．用分别表示学校、小明家、小红家，已知学校在小明家的南偏东，小红家在小明家正东，小红家在学校北偏东，则等于（ ）
A．B．C．D．
8．亚奥理事会于2015年9月16日在土库曼斯坦阿什哈巴德举行第34届代表大会，并在会上投票选出2022年第19届亚运会举办城市为杭州．5个城市的国际标准时间（单位：时）在数轴上表示如图所示，那么北京时间2015年9月16日20时应是（ ）
A．伦敦时间2015年9月16日11时
B．巴黎时间2015年9月16日13时
C．智利时间2015年9月16日5时
D．曼谷时间2015年9月16日18时
9．某商人在一次买卖中均以210元卖出两件衣服，一件赚，一件赔，在这次交易中，该商人（ ）
A．赔28元B．赚28元C．不赚不赔D．无法确定
10．观察并找出图形变化的规律，则第2024个图形中黑色正方形的数量是（ ）
A．2024B．3036C．3035D．3034
二、填空（本大题共6题，每题4分，共24分）
11．比–39大2的数是 ．
12．单项式的系数是 .
13．已知与互余，与互补，，则 ．
14．若单项式与是同类项，则m的值是 ．
15．方程是一元一次方程，则 ．
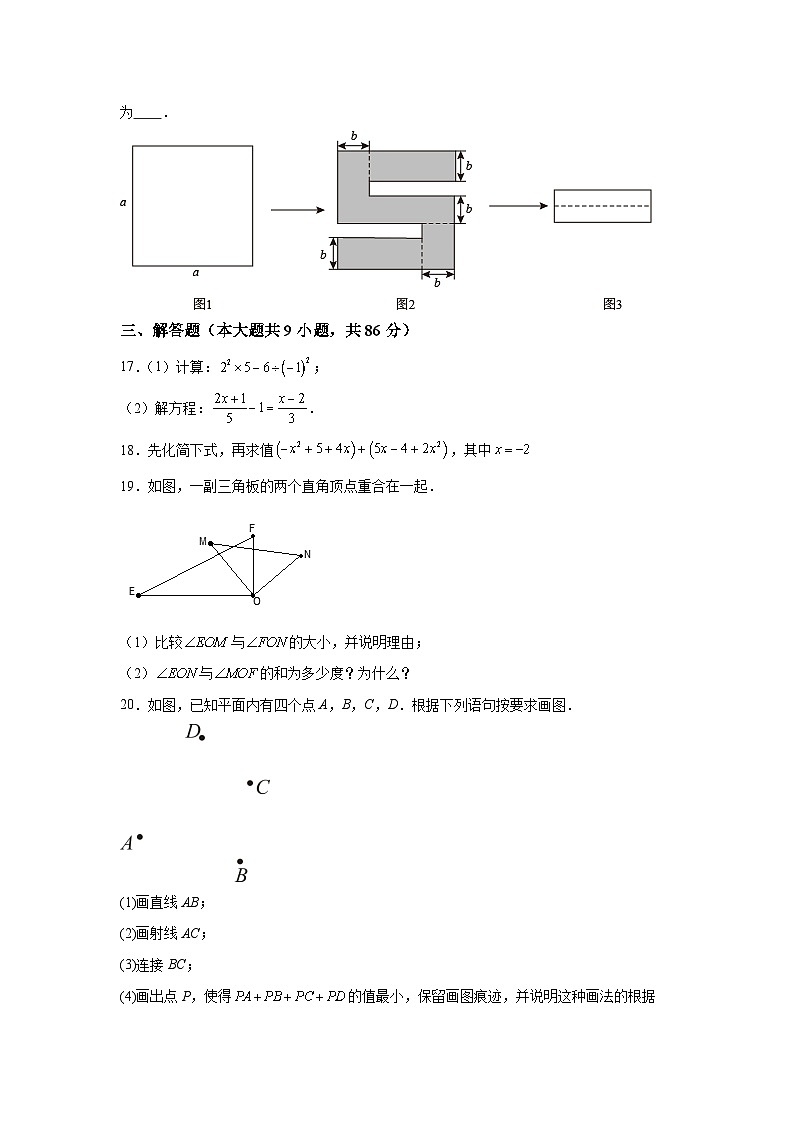
16．如图1，将一个边长为a的正方形纸片剪去两个小矩形，得到一个“”的图案，如图2所示，再将剪下的两个小矩形拼成一个新的矩形，如图3所示，则新矩形的周长可表示为 ．
三、解答题（本大题共9小题，共86分）
17．（1）计算：；
（2）解方程：．
18．先化简下式，再求值，其中
19．如图，一副三角板的两个直角顶点重合在一起．
（1）比较与的大小，并说明理由；
（2）与的和为多少度？为什么？
20．如图，已知平面内有四个点A，B，C，D．根据下列语句按要求画图．
(1)画直线AB；
(2)画射线AC；
(3)连接BC；
(4)画出点P，使得的值最小，保留画图痕迹，并说明这种画法的根据是 ．
21．如图，已知线段上有两点，，且，点，分别为，的中点，．求的长．

22．在罗山县某住房小区建设中，为了提高业主的宜居环境，某小区规划修建一个广场(平面图如图所示)．
(1)用含m、n的代数式表示该广场的面积S；
(2)若m、n满足(m-6)2+|n-8|=0，求出该广场的面积．
23．“龙年大吉，岁岁平安”，为了喜迎2024年新春，长汀某知名豆腐干店推出豆腐干新包装礼盒，新版A型礼盒和B型礼盒．已知A型礼盒的成本为每盒30元，B型礼盒的成本为每盒25元，A型礼盒的售价比B型礼盒的售价多20元，售卖1盒A型礼盒获得的利润和售卖2盒B型礼盒获得的利润一样多．
(1)求每盒A型礼盒和B型礼盒的售价；
(2)该豆腐干店第一批购进了200盒A型礼盒和100盒B型礼盒，为回馈客户该店计划将每盒A型礼盒打折出售，B型礼盒原价出售，售完这批A型礼盒和B型礼盒豆腐干店共盈利1500元，按此计划每盒A型礼盒包装应打几折出售？
24．已知线段，点在线段上，且．
(1)求线段，的长；
(2)点是线段上的动点，线段的中点为，设．
①请用含有的式子表示线段，的长；
②若三个点，，中恰有一点是其它两点所连线段的中点，则称，，三点为“和谐点”，求使得，，三点为“和谐点”的的值．
25．根据以下素材，探索完成任务．
参考答案与解析
1．C
【分析】对于一个绝对值较大的数，用科学记数法写成的形式，其中，n是比原整数位数少1的数．
【详解】解：．
故选C．
【点睛】此题考查了科学记数法的表示方法，科学记数法的表示形式为的形式，其中，n为整数，表示时关键要正确确定a的值以及n的值．
2．D
【分析】先计算，根据绝对值的意义即可求解．正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数．
【详解】解：∵，
∴的绝对值是3，
故选：D．
【点睛】本题考查了求一个数的绝对值，掌握绝对值的意义是解题的关键．
3．C
【详解】A ∵ ﹣8+5=-3 ，故不正确；
B.∵（﹣2）3=-8，故不正确；
C ∵﹣（a﹣b）=﹣a+b，故正确；
D ∵2（a+b）=2a+2b ，故不正确；
故选C
4．B
【分析】正方体的平面展开图中，相对面的特点是之间一定相隔一个正方形，据此作答．
【详解】∵正方体的平面展开图中，相对面的特点是之间一定相隔一个正方形，
∴在此正方体上与“建”字相对的面上的汉字是“百”．
故选B．
【点睛】本题考查了正方体的展开图形，解题关键是从相对面入手进行分析及解答问题．
5．D
【详解】A. ∵bB. ∵b<0，a>0，，∴ a+b＜0，故选项不符合题意；
C. ∵b<0，a>0，ab＜0，故选项不符合题意；
D. ∵a<0，b>0，b>a，故选项符合题意；
故选：D.
6．D
【分析】由与都是的补角可得，进而可得关于m的方程，解方程即可求出m，进一步即可进行判断．
【详解】解：由与都是的补角，得，
即，解得：，
所以．
所以与互为余角且相等．
故选：D．
【点睛】本题考查了余角和补角以及简单的一元一次方程的解法，属于基本题型，熟练掌握上述基础知识是解题的关键．
7．B
【详解】从图中我们会发现∠ACB=180°-∠BAC-∠ABC=180°-60°-65°=55°．故选B．
8．B
【详解】试题分析：选项A，伦敦时间比北京早8时，所以伦敦时间2015年9月16日12时，选项A错误；选项B，巴黎时间比北京早7时，巴黎时间2015年9月16日13时，选项B正确；选项C，智利时间比北京早12时，智利时间2015年9月16日8时，选项C错误；选项D，曼谷时间比北京早1时，曼谷城时间2015年9月16日19时，选项D错误；故答案选B．
考点：数轴．
9．A
【分析】本题考查了一元一次方程的实际应用，掌握一元一次方程解决盈亏问题是解题的关键．首先根据题意计算出赚了的衣服的衣服的进价，然后再计算出赔了的衣服进价，然后再计算出是陪还是赚．
【详解】解：设赚了的衣服进价是x元，
则，
解得元，
则实际赚了元；
设赔了的衣服进价是y元，
则，解得元，
则赔了元；
∵；
∴赔大于赚，在这次交易中，该商人是赔了元,
故选A．
10．B
【分析】本题考查了图形的变化规律，解题的关键是仔细的观察图形并正确的找到规律，解决问题．
【详解】解：∵当n为偶数时第n个图形中黑色正方形的数量为个；
当n为奇数时第n个图形中黑色正方形的数量为个，
∴当时，黑色正方形的个数为(个)，
故选B．
11．-37
【分析】根据题意先列出代数式，计算代数式即可.
【详解】比大的数是：
，
故答案为.
【点睛】本题考查了有理数的加法，解决本题的关键是根据题意列出代数式.
12．－
【分析】单项式的次数:一个单项式中，所有字母的指数的和叫做这个单项式的次数;
单项式的系数:单项式中的数字因数.
【详解】单项式-的系数是: -.
故答案为-
【点睛】本题考核知识点：单项式的系数.解题关键点：理解单项式的系数的意义.
13．
【分析】此题考查了补角和余角的相关计算，熟练掌握互余和互补的定义是解题的关键．先根据与互余，求出，再根据与互补即可得到答案．
【详解】解：∵与互余，，
∴，
∵与互补，
∴，
故答案为：
14．3
【分析】根据同类项的定义：如果两个单项式所含的字母相同，相同字母的指数也相同，那么这两个单项式就叫做同类项，据此求解即可．
【详解】解：∵与是同类项，
∴，
∴，
故答案为：3．
【点睛】本题主要考查了同类项的定义，解题的关键在于能够熟练掌握同类项的定义．
15．
【分析】根据一元一次方程的定义得出，求出即可．
【详解】由题意，得．
所以．
故答案为：．
【点睛】本题考查了一元一次方程的定义，能熟记一元一次方程的定义的内容是解此题的关键．
16．4a﹣8b
【分析】剪下的两个小矩形的长为a-b，宽为 (a-3b)，所以这两个小矩形拼成的新矩形的长为a-b，a-3b, 然后计算这个新矩形的周长．
【详解】解：由已知得新矩形的长是：a-b．新矩形的宽是：a-3b，新矩形的周长是： [(a−b)+(a−3b)]×2 = (2a−4b)×2 =4a-8b．
故答案为：（4a-8b）
【点睛】本题考查了列代数式：把问题中与数量有关的词语，用含有数字、字母和运算符号的式子表示出来，就是列代数式，及整式的运算，解决本题的关键用a和b表示出剪下的两个小矩形的长与宽．
17．（1） （2）
【分析】本题考查有理数的混合运算和解一元一次方程，掌握运算法则是解题的关键．
（1）先算乘方，然后运算乘除法，然后运算减法解题即可；
（2）先去括号，去分母，移项，合并同类项解方程即可．
【详解】解：（1）
；
（2）去分母得：
去括号得：
移项得：
合并同类项得：．
18．，．
【分析】先去括号，再合并同类项，最后代入计算解题．
【详解】解：原式
当时，
原式
．
【点睛】本题考查整式的加减—化简求值，是重要考点，难度较易，掌握相关知识是解题关键．
19．（1）=，理由见解析；（2）+=180º，理由见解析．
【分析】（1）根据等角的余角相等即可发现：两个角相等．
（2）要求∠EON+∠MOF的度数和，结合图形发现角之间的和的关系，显然即是两个直角的和．
【详解】解：（1）∠EOM=∠FON．理由：
∵∠EOM+∠MOF=90°=∠FON+∠MOF，
∴∠EOM=∠FON；
（2）∵∠EON+∠EOF=∠EOM+∠MOF+∠FON+∠MOF，
∴∠EON+∠MOF=∠EOF+∠MON=180°．
20．(1)画图见详解；
(2)画图见详解；
(3)画图见详解；
(4)画图见详解；两点之间线段最短．
【分析】根据直线、射线和线段的特点进行作图：
（1）直线没有端点，向两端无限延伸，如图所示；
（2）射线只有一个端点，向一边无限延伸，如图所示；
（3）线段有两个端点，如图所示；
（4）连接BD交AC于P，根据两点之间线段最短可判断P点满足条件．
【详解】（1）如图，直线AB就是所求的直线；
（2）如图，射线AC就是所求的射线；
（3）如图，BC就是所求的线段；
（4）如图，点P为所作．根据两点之间线段最短可得到此时PA+PB+PC+PD的值最小．
故答案为：两点之间线段最短．
【点睛】此题考查了根据直线、射线、线段的定义进行基本作图，解题的关键是熟悉基本几何作图，知道两点之间线段最短．
21．
【分析】先根据设，则，再利用中点的性质用x表示出的长，然后利用计算出x的值，再利用，就可以得到的长.
【详解】解：因为，
所以设，，．
因为，分别是，的中点，
所以，．
所以，
所以．
所以．
【点睛】本题考查线段的和差，中点定义，巧设未知数表示线段的长是解题的关键．
22．(1)3.5mn；(2)168．
【分析】(1)由广场的面积等于大矩形面积减去小矩形面积表示出即可；
(2)利用非负数的性质求出与的值，代入中计算即可得到结果．
【详解】(1)S=2m×2n–m(2n–n–0.5n)
=4mn–0.5mn
=3.5mn；
(2)由题意得m–6=0，n–8=0，
∴m=6，n=8，
∴原式=3.5×6×8=168．
【点睛】此题考查了整式的加减-化简求值，非负数的性质，不规则图形的面积等知识，解本题的关键是学会利用分割法求不规则图形的面积．
23．(1)每盒A型礼盒和B型礼盒的售价分别为元，元
(2)计划每盒A型礼盒包装应打折出售
【分析】本题考查了一元一次方程的应用，理解题意、找到等量关系并正确列出方程是关键.
（1）设每盒A型礼盒的售价为元， 根据等量关系“售卖1盒A型礼盒获得的利润和售卖2盒B型礼盒获得的利润一样多”即可列出方程，解方程即可；
（2）设计划每盒A型礼盒包装应打折出售，列出方程，即可得出答案；
【详解】（1）解：设每盒A型礼盒的售价为元，
列方程得：，
解得：，
∴B型礼盒的售价为：元，
答：每盒A型礼盒和B型礼盒的售价分别为元，元．
（2）设计划每盒A型礼盒包装应打折出售，依题意得:
，
解得: ，
答：计划每盒A型礼盒包装应打折出售．
24．(1)，
(2)①当点在线段上时，，；当点在线段上时，，；②的值为或
【分析】本题考查两点间的距离，熟练掌握线段中点的定义和线段的和差是解题关键．
（1）由线段，点C在线段上，且，可得答案；
（2）①分当点在线段上时和当点P在线段上两种情况分别计算即可；②分情况列方程可得的值．
【详解】（1）解：解：∵线段，点C在线段上，且，
∴，；
（2）解：①当点在线段上时，
∵点是的中点，
∴，
，；
当点在线段上时，
∵点是的中点，
∴，
，；
②当点在线段上时，则，
∴，
解得：，
当点在线段上时，
则，
∴，
解得：，
综上：的值为或．
25．任务1：，；任务2：；任务3：，，，
【分析】本题主要考查余角和补角定义及三角板有关的角度计算，解题的关键是熟练掌握三角板的各个角度，以及正确画出图形，具有分类讨论的思想．
任务1：利用直角三角形两锐角之和为直角及平角的定义来解题；
任务2：设，通过角的和差关系列出方程求解即可；
任务3：根据题意，画出图形，进行分类讨论即可．
【详解】解：任务1：
∵，
∴，，
∵，
∴，
∴与互余的角有：，；
任务2：∵，
∴可设，
∵，，
∴，
∵是的平分线，
∴，
∴，
∴，
∴，
∴，
任务3：
当与边的夹角为时，
①当在下方时，
，，
；
，
，
②当在上方时，
，，，
；
当与边的夹角为时，
①当在下方时，
，，
，
，
②当在上方时，
，，
，
综上：另一条直角边与边的夹角可能是，，，，
探究三角尺中的学问
素材1
已知点为直线上一点，，.
图1 图2
素材2
如图，三角尺①固定不动，将三角尺②的直角顶点与三角尺①的顶点重合，按三角尺②的一条直角边与边的夹角为摆放.
图3
问题解决
任务1
问题1：如图1，若，图中哪些角与互余？
任务2
问题2：如图2，已知射线是的平分线，且，求的度数；
任务3
问题3：探究当，求三角尺②的另一条直角边与边的夹角的度数，请直接写出探究结论，不必写出探究过程.