2024年高考数学重难点突破讲义：配套热练 特别策划1　空间想象——立体几何问题的几种策略

这是一份2024年高考数学重难点突破讲义：配套热练 特别策划1　空间想象——立体几何问题的几种策略，共7页。
(第1题)
A．0°B．45°
C．60°D．90°
【解析】 如图，连接A1D，BD，A1B，因为在正方体ABCD－A1B1C1D1中，点E，F分别是AA1，AD的中点，EF∥A1D．因为A1B∥D1C，所以∠DA1B是CD1与EF所成角．因为A1D＝A1B＝BD，所以∠DA1B＝60°，所以CD1与EF所成角为60°．
(第1题)
2．将边长为eq \r(,2)的正方形ABCD沿对角线BD折起，则三棱锥C－ABD的外接球体积为( C )
A．eq \f(32π,3)B．eq \f(16π,3)
C．eq \f(4π,3)D．4π
【解析】 将边长为eq \r(,2)的正方形ABCD沿对角线BD折起，得到三棱锥C－ABD，如图所示，则BC⊥CD，BA⊥AD，取BD中点O，连接OA，OC，则OA＝OB＝OC＝OD，三棱锥C－ABD的外接球直径为BD＝2，外接球的体积为eq \f(4,3)πR3＝eq \f(4,3)π．
(第2题)
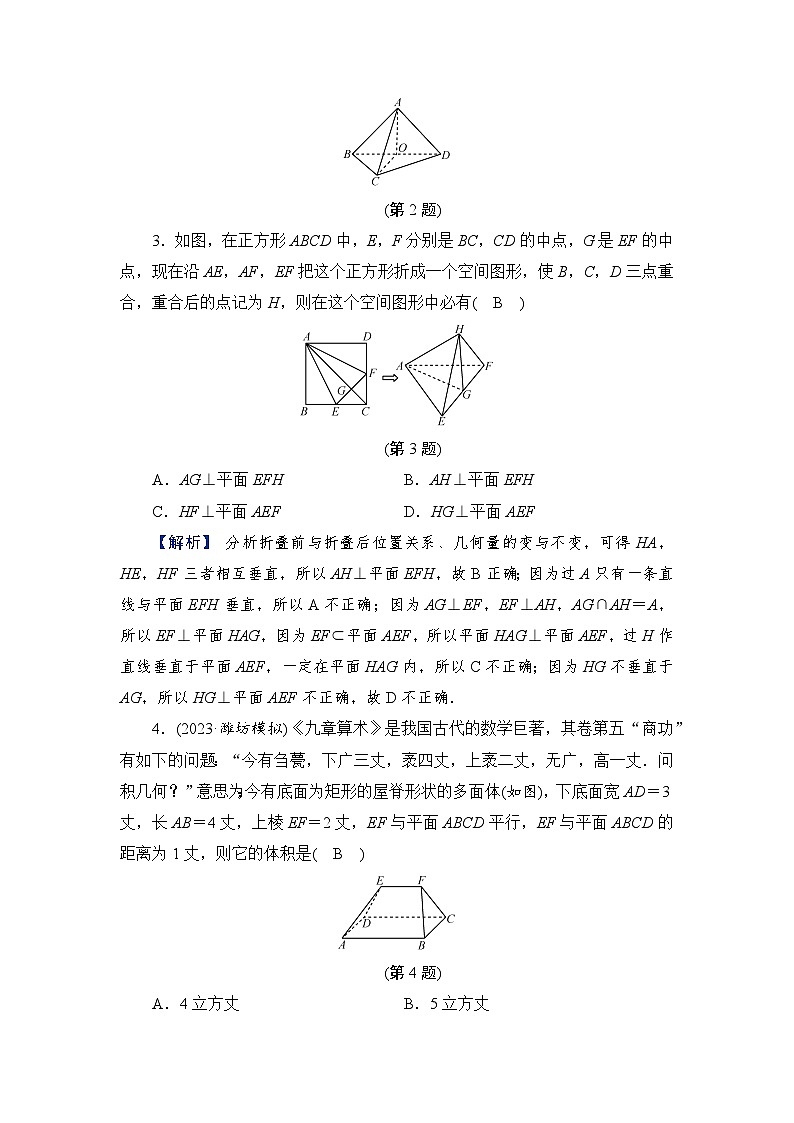
3．如图，在正方形ABCD中，E，F分别是BC，CD的中点，G是EF的中点，现在沿AE，AF，EF把这个正方形折成一个空间图形，使B，C，D三点重合，重合后的点记为H，则在这个空间图形中必有( B )
(第3题)
A．AG⊥平面EFHB．AH⊥平面EFH
C．HF⊥平面AEFD．HG⊥平面AEF
【解析】 分析折叠前与折叠后位置关系、几何量的变与不变，可得HA，HE，HF三者相互垂直，所以AH⊥平面EFH，故B正确；因为过A只有一条直线与平面EFH垂直，所以A不正确；因为AG⊥EF，EF⊥AH，AG∩AH＝A，所以EF⊥平面HAG，因为EF⊂平面AEF，所以平面HAG⊥平面AEF，过H作直线垂直于平面AEF，一定在平面HAG内，所以C不正确；因为HG不垂直于AG，所以HG⊥平面AEF不正确，故D不正确．
4．(2023·潍坊模拟)《九章算术》是我国古代的数学巨著，其卷第五“商功”有如下的问题：“今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高一丈．问积几何？”意思为：今有底面为矩形的屋脊形状的多面体(如图)，下底面宽AD＝3丈，长AB＝4丈，上棱EF＝2丈，EF与平面ABCD平行，EF与平面ABCD的距离为1丈，则它的体积是( B )
(第4题)
A．4立方丈B．5立方丈
C．6立方丈D．8立方丈
【解析】 如图，过E作EG⊥平面ABCD，垂足为G，过F作FH⊥平面ABCD，垂足为H，过G作PQ∥AD，交AB于Q，交CD于P，过H作MN∥BC，交AB于N，交CD于M，由图形的对称性可知，AQ＝BN＝1丈，QN＝2丈，且四边形AQPD与四边形NBCM都是矩形，则它的体积V＝VE－AQPD＋VEPQ－FMN＋VF－NBCM＝eq \f(1,3)·EG·S矩形AQPD＋S△EPQ·NQ＋eq \f(1,3)·FH·S矩形NBCM＝eq \f(1,3)×1×1×3＋eq \f(1,2)×3×1×2＋eq \f(1,3)×1×1×3＝5(立方丈)．
(第4题)
5．如图，已知正方体ABCD－A1B1C1D1，M为AA1上一点，A1M∶MA＝3∶1，则截面B1D1M与底面ABCD所成二面角的余弦值为( D )
(第5题)
A．eq \f(\r(,17),17)B．eq \f(\r(,34),17)
C．eq \f(2\r(,17),17)D．eq \f(2\r(,34),17)
【解析】 设正方体ABCD－A1B1C1D1的棱长为a．由正方体的性质知，点B1，D1，M在底面射影分别为B，D，A．因为△B1D1M在底面的射影为△ABD，且S△ABD＝eq \f(1,2)a2，而△B1D1M为等腰三角形，A1M＝eq \f(3,4)a，B1D1＝eq \r(,2)a，则MB1＝eq \f(5,4)a．设B1D1的中点为O，则MO＝eq \f(\r(,17),4)a，故S△B1D1M＝eq \f(\r(,34),8)a2，截面B1D1M与底面ABCD所成二面角为θ，由二面角的面积射影公式知csθ＝eq \f(S△ABD,S△B1D1M)＝eq \f(\f(1,2)a2,\f(\r(,34),8)a2)＝eq \f(2\r(,34),17)．
6．(2023·福州检测)如图，在正三棱柱ABC－A1B1C1中，AB＝AA1＝2，F是线段A1B1上的动点，则AF＋FC1的最小值为__eq \r(,6)＋eq \r(,2)__．
(第6题)
【解析】 将正三棱柱ABC－A1B1C1中的△A1B1C1沿A1B1翻折至平面ABB1A1上，如图所示，连接AC1，则AF＋FC1≥AC1．因为AA1＝A1C1＝2，且∠AA1C1＝90°＋60°＝150°，所以AC1＝2AA1·sineq \f(∠AA1C1,2)＝2×2sin 75°＝4sin(30°＋45°)＝4×(sin 30°cs 45°＋cs 30°sin 45°)＝eq \r(,6)＋eq \r(,2)，所以当A，F，C1三点共线时，AF＋FC1取得最小值，为eq \r(,6)＋eq \r(,2)．
(第6题)
7．已知在直三棱柱ABC－A1B1C1中，∠ABC＝120°，AB＝2，BC＝CC1＝1，则异面直线AB1与BC1所成角的余弦值为__eq \f(\r(,10),5)__．
【解析】 如图，将直三棱柱ABC－A1B1C1补形为直四棱柱ABCD－A1B1C1D1，连接AD1，B1D1，BD．由题意知∠ABC＝120°，AB＝2，BC＝CC1＝1，所以AD1＝BC1＝eq \r(,2)，AB1＝eq \r(,5)，∠DAB＝60°．在△ABD中，由余弦定理知BD2＝22＋12－2×2×1×cs 60°＝3，所以BD＝eq \r(,3)，所以B1D1＝eq \r(,3)．因为ADeq \\al(2,1)＋B1Deq \\al(2,1)＝ABeq \\al(2,1)，所以∠AD1B1＝90°，所以AB1与BC1所成的角即为AB1与AD1所成的角，其余弦值为cs∠B1AD1＝eq \f(AD1,AB1)＝eq \f(\r(,10),5)．
(第7题)
8．在棱长为1的正方体ABCD－A1B1C1D1中，E是CC1的中点，F在BB1上且BF＝eq \f(1,3)BB1，则平面A1EF与底面ABCD所成二面角的余弦值为__eq \f(6\r(,53),53)__．
【解析】 如图，△A1EF在平面ABCD上的射影是△ABC．设所求二面角为θ，则cs θ＝eq \f(S△ABC,S△A1EF)，其中A1E＝eq \f(3,2)，A1F＝eq \f(\r(,13),3)，EF＝eq \f(\r(,37),6)，cs∠EA1F＝eq \f(8,3\r(,13))，sin∠EA1F＝eq \f(\r(,53),3\r(,13))，S△A1EF＝eq \f(1,2)A1F·A1E·sin∠EA1F＝eq \f(\r(,53),12)，所以cs θ＝eq \f(S△ABC,S△A1EF)＝eq \f(6\r(,53),53)，即所求二面角的余弦值为eq \f(6\r(,53),53)．
(第8题)
9．把如图所示的平面图形分别沿AB，BC，AC翻折，已知D1，D2，D3三点始终可以重合于点D得到三棱锥D－ABC，那么当该三棱锥体积最大时，其外接球的表面积为__50π__．
(第9题)
【解析】 如图，在三棱锥D－ABC中，当且仅当DA⊥平面ABC时，三棱锥的体积达到最大，此时，设外接球的半径为R，球心为O，球心O到平面ABC的投影点为F，则有R2＝OA2＝OF2＋AF2，又OF＝eq \f(1,2)AD＝eq \f(5,2)，AF＝eq \f(1,2)AC＝eq \f(5,2)，所以R2＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,2)))2＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,2)))2＝eq \f(25,2)，所以外接球的表面积为S＝4πR2＝4π×eq \f(25,2)＝50π．
(第9题)
10．如图，在直三棱柱ABC－A1B1C1中，棱柱的侧面均为矩形，AA1＝1，AB＝BC＝eq \r(,3)，cs∠ABC＝eq \f(1,3)，P是A1B上的一动点，则AP＋PC1的最小值为__eq \r(,7)__．
(第10题)
【解析】 连接BC1，得△A1BC1，以A1B所在直线为轴，将△A1BC1所在平面旋转到平面ABB1A1，设点C1的新位置为C′，连接AC′，则有AP＋PC1＝AP＋PC′≥AC′，如图，当A，P，C′三点共线时，则AC′即为AP＋PC1的最小值．在△ABC中，AB＝BC＝eq \r(,3)，cs∠ABC＝eq \f(1,3)，由余弦定理得AC＝eq \r(,AB2＋BC2－2AB·BCcs∠ABC)＝eq \r(,3＋3－2×3×\f(1,3))＝2，所以A1C1＝2，即A1C′＝2，在△A1AB中，AA1＝1，AB＝eq \r(,3)，由勾股定理可得A1B＝eq \r(,AA\\al(2,1)＋AB2)＝eq \r(,1＋3)＝2，且∠AA1B＝60°．同理可求C1B＝2，因为A1B＝BC1＝A1C1＝2，所以△A1BC1为等边三角形，所以∠BA1C1＝60°，所以在△AA1C′中，∠AA1C′＝∠AA1B＋∠BA1C′＝120°，AA1＝1，A1C′＝2，由余弦定理得AC′＝eq \r(,1＋4－2×1×2×\b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2))))＝eq \r(,7)．

(第10题)