2023-2024学年河南省信阳市羊山新区九年级（上）期末数学试卷

这是一份2023-2024学年河南省信阳市羊山新区九年级（上）期末数学试卷，共19页。
A．B．
C．D．
2．（3分）抛物线y＝2（x﹣3）2+1的顶点坐标是（ ）
A．（3，1）B．（3，﹣1）C．（﹣3，1）D．（﹣3，﹣1）
3．（3分）一元二次方程x2+x﹣1＝0的根的情况是（ ）
A．有两个不相等的实数根
B．没有实数根
C．有两个相等的实数根
D．只有一个实数根
4．（3分）为验证“掷一个质地均匀的骰子，向上的点数为偶数的概率是0.5”，下列模拟试验中，不科学的是（ ）
A．袋中装有1个红球一个绿球，它们除颜色外都相同，计算随机摸出红球的概率
B．用计算器随机地取不大于10的正整数，计算取得奇数的概率
C．随机掷一枚质地均匀的硬币，计算正面朝上的概率
D．如图，将一个可以自由旋转的转盘分成甲、乙、丙3个相同的扇形，转动转盘任其自由停止，计算指针指向甲的概率
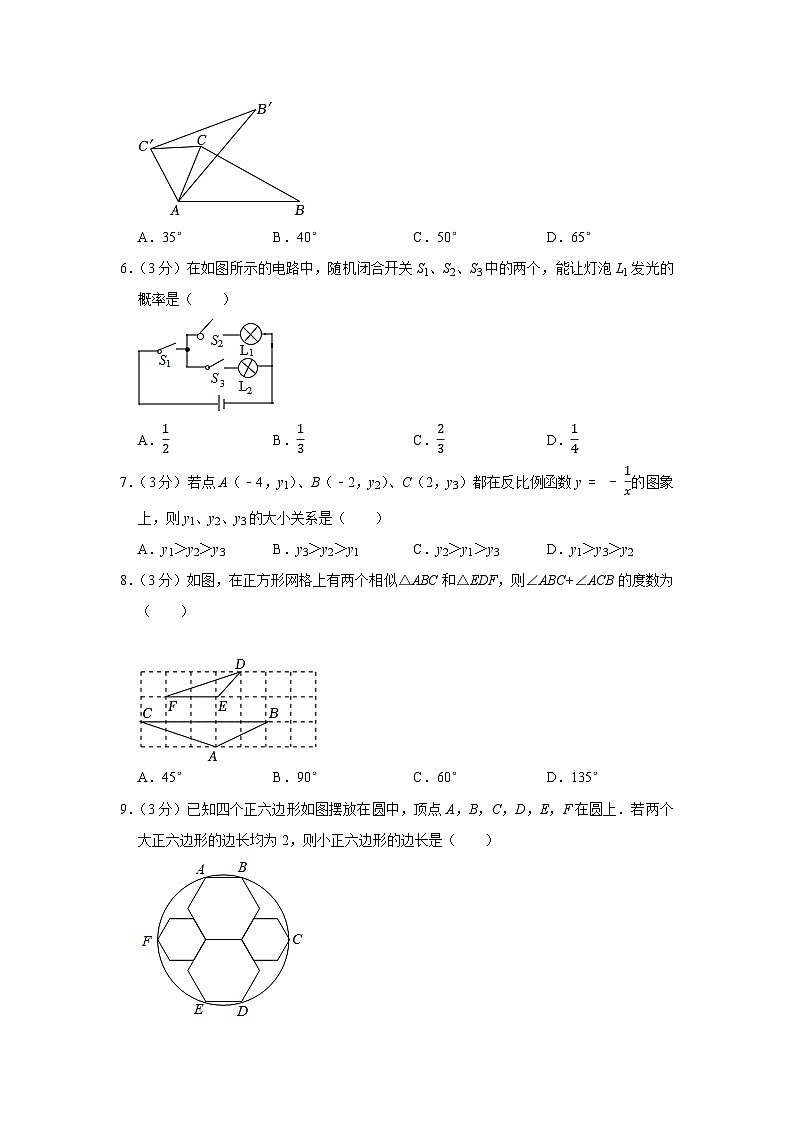
5．（3分）如图，在△ABC中，∠CAB＝65°，将△ABC在平面内绕点A旋转到△AB'C'的位置，使CC'∥AB，则旋转角的度数为（ ）
A．35°B．40°C．50°D．65°
6．（3分）在如图所示的电路中，随机闭合开关S1、S2、S3中的两个，能让灯泡L1发光的概率是（ ）
A．12B．13C．23D．14
7．（3分）若点A（﹣4，y1）、B（﹣2，y2）、C（2，y3）都在反比例函数y=-1x的图象上，则y1、y2、y3的大小关系是（ ）
A．y1＞y2＞y3B．y3＞y2＞y1C．y2＞y1＞y3D．y1＞y3＞y2
8．（3分）如图，在正方形网格上有两个相似△ABC和△EDF，则∠ABC+∠ACB的度数为（ ）
A．45°B．90°C．60°D．135°
9．（3分）已知四个正六边形如图摆放在圆中，顶点A，B，C，D，E，F在圆上．若两个大正六边形的边长均为2，则小正六边形的边长是（ ）
A．3-3B．23-12C．3+12D．13-12
10．（3分）如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，翻折∠B，使点B落在直角边AC上某一点D处，折痕为EF，点E、F分别在边BC、AB上，若△CDE与△ABC相似，则CE的长为（ ）
A．169B．34C．34或169D．32或169
二、填空题（每题3分，本大题共5小题，共30分。）
11．（3分）反比例函数y=m-5x的图象在第二、四象限内，那么m的取值范围是 ．
12．（3分）方程(a-2)xa2-2+3x=0是关于x的一元二次方程，则a的值为 ．
13．（3分）根据物理学规律，如果不考虑空气阻力，以40m/s的速度将小球沿与地面成30°角的方向击出，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间的函数关系是：h＝﹣5t2+20t，则小球运动中的最大高度是 m．
14．（3分）喜迎党的二十大召开，学校推荐了四部影片：《1921》、《香山叶正红》、《建党伟业》、《建军大业》．甲、乙同学用抽卡片的方式决定本班观看哪部，四张卡片正面分别是上述影片剧照，除此之外完全相同．将这四张卡片背面朝上，甲随机抽出一张并放回，洗匀后，乙再随机抽出一张，则两人恰好抽到同一部的概率是 ．
15．（3分）如图，在边长为4的正方形ABCD中，以AB为直径的半圆交对角线AC于点E，以C为圆心、BC长为半径画弧交AC于点F，则图中阴影部分的面积是 ．
三、解答题（本大题共6小题，共30分。）
16．（10分）用适当的方法解下列方程：
（1）（x﹣1）2＝4；
（2）x2﹣3x﹣4＝0．
17．（9分）为了保护学生视力，防止学生沉迷网络和游戏，促进学生身心健康发展，教育办公厅于2021年1月15日颁发了《教育部办公厅关于加强中小学生手机管理工作的通知》为贯彻《通知》精神，学校组织该主题漫画比赛．现在小雪和小英想通过设计一个游戏来决定谁去参赛．游戏规则如下：有一个可自由转动的转盘，被分成了三个大小相同的扇形，分别标有数字2，3，4；另有一个不透明的瓶子，装有分别标有数字1，3，5的三个完全相同的小球．先转动一次转盘，停止后记下指针指向的数字（若指针指在分界线上则重转），再从瓶子中随机取出一个小球，记下小球上的数字．若得到的两数字之和大于6，则小雪参赛；若得到的两数字之和小于6，则小英参赛．
（1）请用列表或画树状图的方法表示出所有可能出现的结果；
（2）此游戏公平吗？请说明理由．
18．（9分）如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，3），B（2，5），C（4，2）（每个方格的边长均为1个单位长度）
（1）将△ABC平移，使点A移动到点A1，请画出△A1B1C1；
（2）作出△ABC关于O点成中心对称的△A2B2C2，并直接写出A2，B2，C2的坐标；
（3）△A1B1C1与△A2B2C2是否成中心对称？若是，请写出对称中心的坐标；若不是，请说明理由．
19．（9分）实验数据显示，一般成人喝半斤低度白酒后，1.5小时内其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y＝﹣200x2+400x刻画；1.5小时后（包括1.5小时）y与x可近似地用反比例函数y=kx（k＞0）刻画（如图所示）．
（1）根据上述数学模型计算：
①喝酒后几时血液中的酒精含量达到最大值？最大值为多少？
②当x＝5时，y＝45，求k的值．
（2）按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”，不能驾车上路．参照上述数学模型，假设某驾驶员晚上20：00在家喝完半斤低度白酒，第二天早上7：00能否驾车去上班？请说明理由．
20．（9分）阅读下面材料，完成学习任务：
数学活动 测量树的高度
在物理学中我们学过光的反射定律．数学综合实践小组想利用光的反射定律测量池塘对岸一棵树的高度AB测量和计算的部分步骤如下：
①如图，在地面上的点C处放置了一块平面镜，小华站在BC的延长线上，当小华从平面镜中刚好看到树的顶点A时．测得小华到平面镜的距离CD＝2米，小华的眼睛E到地面的距离ED＝1.5米；
②将平面镜从点C沿BC的延长线向后移动10米到点F处，小华向后移动到点H处时，小华的眼睛G又刚好在平面镜中看到树的顶点A，这时测得小华到平面镜的距离FH＝3米；
③计算树的高度AB：设AB＝x米，BC＝y米．
∵∠ABC＝∠EDC＝90°，∠ACB＝∠ECD
∴△ABC∽△EDC
∴ABED=BCDC⋯⋯
任务：请你根据材料中得到的测量数据和计算步骤，将剩余的计算部分补充完整．
21．（9分）如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC＝BD，连接AC，过点D作DE⊥AC，垂足为E．
（1）求证：AB＝AC；
（2）求证：DE为⊙O的切线；
（3）若⊙O的半径为5，∠BAC＝60°，求DE的长．
2023-2024学年河南省信阳市羊山新区九年级（上）期末数学试卷
参考答案与试题解析
一.选择题（每小题3分，共30分）
1．（3分）数学世界奇妙无穷，其中曲线是微分几何的研究对象之一，下列数学曲线是中心对称图形的是（ ）
A．B．
C．D．
【解答】解：选项A、B、D都不能找到这样的一个点，使图形绕某一点旋转180°后与原来的图形重合，所以不是中心对称图形，
选项C能找到这样的一个点，使图形绕某一点旋转180°后与原来的图形重合，所以是中心对称图形，
故选：C．
2．（3分）抛物线y＝2（x﹣3）2+1的顶点坐标是（ ）
A．（3，1）B．（3，﹣1）C．（﹣3，1）D．（﹣3，﹣1）
【解答】解：由y＝2（x﹣3）2+1，根据顶点式的坐标特点可知，顶点坐标为（3，1）．
故选：A．
3．（3分）一元二次方程x2+x﹣1＝0的根的情况是（ ）
A．有两个不相等的实数根
B．没有实数根
C．有两个相等的实数根
D．只有一个实数根
【解答】解：在一元二次方程x2+x﹣1＝0中，
a＝1，b＝1，c＝﹣1，
∴Δ＝b2﹣4ac＝12﹣4×1×（﹣1）＝1+4＝5＞0，
∴原方程有两个不相等的实数根．
故选：A．
4．（3分）为验证“掷一个质地均匀的骰子，向上的点数为偶数的概率是0.5”，下列模拟试验中，不科学的是（ ）
A．袋中装有1个红球一个绿球，它们除颜色外都相同，计算随机摸出红球的概率
B．用计算器随机地取不大于10的正整数，计算取得奇数的概率
C．随机掷一枚质地均匀的硬币，计算正面朝上的概率
D．如图，将一个可以自由旋转的转盘分成甲、乙、丙3个相同的扇形，转动转盘任其自由停止，计算指针指向甲的概率
【解答】解：A、袋中装有1个红球一个绿球，它们出颜色外都相同，随机摸出红球的概率是12，故本选项科学；
B、用计算器随机地取不大于10的正整数，取得奇数的概率是12，故本选项科学；
C、随机掷一枚质地均匀的硬币，正面朝上的概率是12，故本选项科学；
D、将一个可以自由旋转的转盘分成甲、乙、丙3个相同的扇形，转动转盘任其自由停止，指针指向甲的概率是13，故本选项不科学；
故选：D．
5．（3分）如图，在△ABC中，∠CAB＝65°，将△ABC在平面内绕点A旋转到△AB'C'的位置，使CC'∥AB，则旋转角的度数为（ ）
A．35°B．40°C．50°D．65°
【解答】解：由旋转的性质得AC＝AC′．
∵CC′∥AB，∠CAB＝65°，
∴∠C′CA＝∠CAB＝65°．
∵AC＝AC′，
∴∠CC′A＝65°，
∴∠C′AC＝180°﹣2∠CC′A＝180°﹣2×65°＝50°．
故选：C．
6．（3分）在如图所示的电路中，随机闭合开关S1、S2、S3中的两个，能让灯泡L1发光的概率是（ ）
A．12B．13C．23D．14
【解答】解：画树状图得：
∵共有6种等可能的结果，能让灯泡L1发光的有2种情况，
∴能让灯泡L1发光的概率为26=13．
故选：B．
7．（3分）若点A（﹣4，y1）、B（﹣2，y2）、C（2，y3）都在反比例函数y=-1x的图象上，则y1、y2、y3的大小关系是（ ）
A．y1＞y2＞y3B．y3＞y2＞y1C．y2＞y1＞y3D．y1＞y3＞y2
【解答】解：∵点A（﹣4，y1）、B（﹣2，y2）、C（2，y3）都在反比例函数y=-1x的图象上，
∴y1=-1-4=14，y2=-1-2=12，y3=-12，
又∵-12＜14＜12，
∴y3＜y1＜y2．
故选：C．
8．（3分）如图，在正方形网格上有两个相似△ABC和△EDF，则∠ABC+∠ACB的度数为（ ）
A．45°B．90°C．60°D．135°
【解答】解：∵AB=12+22=5、AC=12+32=10，BC＝5，DE=2、EF＝2，DF=10，
∴ABDE=ACEF=BCDF=102，
∴△ABC∽△DEF，
∴∠BAC＝∠DEF＝180°﹣45°＝135°，
∴∠ABC+∠ACB＝180°﹣∠BAC＝45°．
故选：D．
9．（3分）已知四个正六边形如图摆放在圆中，顶点A，B，C，D，E，F在圆上．若两个大正六边形的边长均为2，则小正六边形的边长是（ ）
A．3-3B．23-12C．3+12D．13-12
【解答】解：连接AD交PM于O，则点O是圆心，过点O作ON⊥DE于N，连接MF，取MF的中点G，连接GH，GQ，
由对称性可知，OM＝OP＝EN＝DN＝1，
由正六边形的性质可得ON＝23，
∴OD=DN2+ON2=13=OF，
∴MF=13-1，
由正六边形的性质可知，△GFH、△GHQ、△GQM都是正三角形，
∴FH=12MF=13-12，
故选：D．
10．（3分）如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，翻折∠B，使点B落在直角边AC上某一点D处，折痕为EF，点E、F分别在边BC、AB上，若△CDE与△ABC相似，则CE的长为（ ）
A．169B．34C．34或169D．32或169
【解答】解：由题意可得，
当△CDE∽△CBA时，
则CECA=DEBA，
∵∠C＝90°，AC＝3，BC＝4，翻折∠B，使点B落在直角边AC上某一点D处，
∴AB＝5，BE＝DE，BE＝4﹣CE，
∴CE3=4-CE5，
解得CE=32；
当△CDE∽△CAB时，
则CECB=DEAB，
∵∠C＝90°，AC＝3，BC＝4，翻折∠B，使点B落在直角边AC上某一点D处，
∴AB＝5，BE＝DE，BE＝4﹣CE，
∴CE4=4-CE5，
解得CE=169；
由上可得，CE的长为32或169，
故选：D．
二、填空题（每题3分，本大题共5小题，共30分。）
11．（3分）反比例函数y=m-5x的图象在第二、四象限内，那么m的取值范围是 m＜5 ．
【解答】解：∵反比例函数y=m-5x的图象在第二、四象限内
∴m﹣5＜0，
解得，m＜5；
故答案为：m＜5．
12．（3分）方程(a-2)xa2-2+3x=0是关于x的一元二次方程，则a的值为 ﹣2 ．
【解答】解：由题意得，a﹣2≠0且a2﹣2＝2．
∴a＝﹣2．
故答案为：﹣2．
13．（3分）根据物理学规律，如果不考虑空气阻力，以40m/s的速度将小球沿与地面成30°角的方向击出，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间的函数关系是：h＝﹣5t2+20t，则小球运动中的最大高度是 20 m．
【解答】解：h＝﹣5t2+20t＝﹣5（t﹣2）2+20，
∵﹣5＜0，
∴当t＝2时，h有最大值，最大值为20，
故答案为：20．
14．（3分）喜迎党的二十大召开，学校推荐了四部影片：《1921》、《香山叶正红》、《建党伟业》、《建军大业》．甲、乙同学用抽卡片的方式决定本班观看哪部，四张卡片正面分别是上述影片剧照，除此之外完全相同．将这四张卡片背面朝上，甲随机抽出一张并放回，洗匀后，乙再随机抽出一张，则两人恰好抽到同一部的概率是 14 ．
【解答】解：把影片剧照《1921》、《香山叶正红》、《建党伟业》、《建军大业》的四张卡片分别记为A、B、C、D，
画树状图如下：
共有16种等可能的结果，其中甲、乙两人恰好抽到同一部的结果有4种，
∴甲、乙两人恰好抽到同一部的概率为416=14，
故答案为：14．
15．（3分）如图，在边长为4的正方形ABCD中，以AB为直径的半圆交对角线AC于点E，以C为圆心、BC长为半径画弧交AC于点F，则图中阴影部分的面积是 3π﹣6 ．
【解答】解：连接BE，
∵AB为直径，
∴BE⊥AC，
∵AB＝BC＝4，∠ABC＝90°，
∴BE＝AE＝CE，
∴S弓形AE＝S弓形BE，
∴图中阴影部分的面积＝S半圆-12（S半圆﹣S△ABE）﹣（S△ABC﹣S扇形CBF）
=12π×22-12（12π×22-12×12×4×4）﹣（12×4×4-45π×42360）
＝3π﹣6，
故答案为3π﹣6．
三、解答题（本大题共6小题，共30分。）
16．（10分）用适当的方法解下列方程：
（1）（x﹣1）2＝4；
（2）x2﹣3x﹣4＝0．
【解答】解：（1）（x﹣1）2＝4，
x﹣1＝±2，
∴x﹣1＝2或x﹣1＝﹣2，
∴x1＝3，x2＝﹣1；
（2）x2﹣3x﹣4＝0，
（x﹣4）（x+1）＝0，
∴x﹣4＝0或x+1＝0，
∴x1＝4，x2＝﹣1．
17．（9分）为了保护学生视力，防止学生沉迷网络和游戏，促进学生身心健康发展，教育办公厅于2021年1月15日颁发了《教育部办公厅关于加强中小学生手机管理工作的通知》为贯彻《通知》精神，学校组织该主题漫画比赛．现在小雪和小英想通过设计一个游戏来决定谁去参赛．游戏规则如下：有一个可自由转动的转盘，被分成了三个大小相同的扇形，分别标有数字2，3，4；另有一个不透明的瓶子，装有分别标有数字1，3，5的三个完全相同的小球．先转动一次转盘，停止后记下指针指向的数字（若指针指在分界线上则重转），再从瓶子中随机取出一个小球，记下小球上的数字．若得到的两数字之和大于6，则小雪参赛；若得到的两数字之和小于6，则小英参赛．
（1）请用列表或画树状图的方法表示出所有可能出现的结果；
（2）此游戏公平吗？请说明理由．
【解答】解：（1）画树状图如下：
共有9种等可能的结果；
（2）此游戏公平，理由如下：
共有9种等可能的结果，两数字之和大于6的结果有4种，两数字之和小于6的结果有4种，
∴小雪参赛的概率为49，小英参赛的概率为49，
∴此游戏公平．
18．（9分）如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，3），B（2，5），C（4，2）（每个方格的边长均为1个单位长度）
（1）将△ABC平移，使点A移动到点A1，请画出△A1B1C1；
（2）作出△ABC关于O点成中心对称的△A2B2C2，并直接写出A2，B2，C2的坐标；
（3）△A1B1C1与△A2B2C2是否成中心对称？若是，请写出对称中心的坐标；若不是，请说明理由．
【解答】解：（1）如图，△A1B1C1为所作；
（2）如图，△A2B2C2为所作；点A2，B2，C2的坐标分别为（﹣1，﹣3），（﹣2，﹣5），（﹣4，﹣2）；
（3）△A1B1C1与△A2B2C2关于点P中心对称，如图，
对称中心的坐标的坐标为（﹣2，﹣1）．
19．（9分）实验数据显示，一般成人喝半斤低度白酒后，1.5小时内其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y＝﹣200x2+400x刻画；1.5小时后（包括1.5小时）y与x可近似地用反比例函数y=kx（k＞0）刻画（如图所示）．
（1）根据上述数学模型计算：
①喝酒后几时血液中的酒精含量达到最大值？最大值为多少？
②当x＝5时，y＝45，求k的值．
（2）按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”，不能驾车上路．参照上述数学模型，假设某驾驶员晚上20：00在家喝完半斤低度白酒，第二天早上7：00能否驾车去上班？请说明理由．
【解答】解：（1）①y＝﹣200x2+400x＝﹣200（x﹣1）2+200，
∴x＝1时血液中的酒精含量达到最大值，最大值为200（毫克/百毫升）；
②∵当x＝5时，y＝45，y=kx（k＞0），
∴k＝xy＝45×5＝225；
（2）不能驾车上班；
理由：∵晚上20：00到第二天早上7：00，一共有11小时，
∴将x＝11代入y=225x，则y=22511＞20，
∴第二天早上7：00不能驾车去上班．
20．（9分）阅读下面材料，完成学习任务：
数学活动 测量树的高度
在物理学中我们学过光的反射定律．数学综合实践小组想利用光的反射定律测量池塘对岸一棵树的高度AB测量和计算的部分步骤如下：
①如图，在地面上的点C处放置了一块平面镜，小华站在BC的延长线上，当小华从平面镜中刚好看到树的顶点A时．测得小华到平面镜的距离CD＝2米，小华的眼睛E到地面的距离ED＝1.5米；
②将平面镜从点C沿BC的延长线向后移动10米到点F处，小华向后移动到点H处时，小华的眼睛G又刚好在平面镜中看到树的顶点A，这时测得小华到平面镜的距离FH＝3米；
③计算树的高度AB：设AB＝x米，BC＝y米．
∵∠ABC＝∠EDC＝90°，∠ACB＝∠ECD
∴△ABC∽△EDC
∴ABED=BCDC⋯⋯
任务：请你根据材料中得到的测量数据和计算步骤，将剩余的计算部分补充完整．
【解答】解：设AB＝x米，BC＝y米．
∵∠ABC＝∠EDC＝90°，∠ACB＝∠ECD
∴△ABC∽△EDC
∴ABED=BCDC，
∴x1.5=y2，
∵∠ABF＝∠GHF＝90°，∠AFB＝∠GFH
∴△ABF∽△GHF，
∴ABGH=BFHF，
∴x1.5=y+103，
∴y2=y+103，
解得y＝20，
把y＝20代入x1.5=y2中，
得x1.5=202解得x＝15
∴树的高度AB为15米．
21．（9分）如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC＝BD，连接AC，过点D作DE⊥AC，垂足为E．
（1）求证：AB＝AC；
（2）求证：DE为⊙O的切线；
（3）若⊙O的半径为5，∠BAC＝60°，求DE的长．
【解答】（1）证明：∵AB是⊙O的直径，
∴∠ADB＝90°；
∵BD＝CD，
∴AD是BC的垂直平分线．
∴AB＝AC．（3分）
（2）证明：连接OD，
∵点O、D分别是AB、BC的中点，
∴OD∥AC．
∵DE⊥AC，
∴OD⊥DE．
∴DE为⊙O的切线．（6分）
（3）解：由AB＝AC，∠BAC＝60°知△ABC是等边三角形，
∵⊙O的半径为5，
∴AB＝BC＝10，CD=12BC＝5．
∵∠C＝60°，
∴DE＝CD•sin60°=532．（9分）