北师大版八年级下册5 一元一次不等式与一次函数课前预习ppt课件

这是一份北师大版八年级下册5 一元一次不等式与一次函数课前预习ppt课件，共16页。PPT课件主要包含了x-5，x+60，23x+6≤0，X-2，4–x+30，x≤3，X≤-2，即y0，即y≤0，即y≥0等内容，欢迎下载使用。

1.解不等式2x－5＞0，并把他的解集在数轴上表示出来
2. 一次函数 y = 2x – 5的图像与x轴的交点坐标是 ，与y轴的交点 坐标是 。要作这个函数的图像只要描出_____个点。
下面我们来探讨一下一元一次不等式与一次函数之间的关系
理解一次函数图象与一元一次不等式的关系
能够用图像法解一元一次不等式
理解两种方法的关系，会选择适当的方法解一元一次不等式　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　
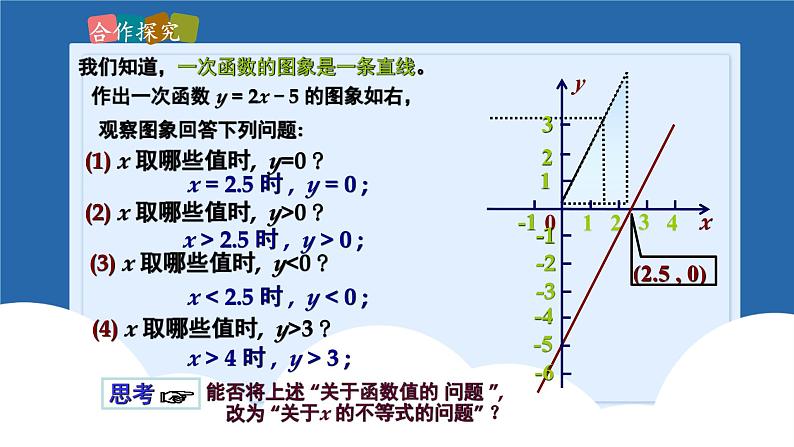
我们知道，一次函数的图象是一条直线。
作出一次函数 y = 2x - 5 的图象如右，
观察图象回答下列问题:
(1) x 取哪些值时, y=0 ?
(2) x 取哪些值时, y>0 ?
x > 2.5 时 , y > 0 ;
x = 2.5 时 , y = 0 ;
(3) x 取哪些值时, y<0 ?
x < 2.5 时 , y < 0 ;
(4) x 取哪些值时, y>3 ?
x > 4 时 , y > 3 ;
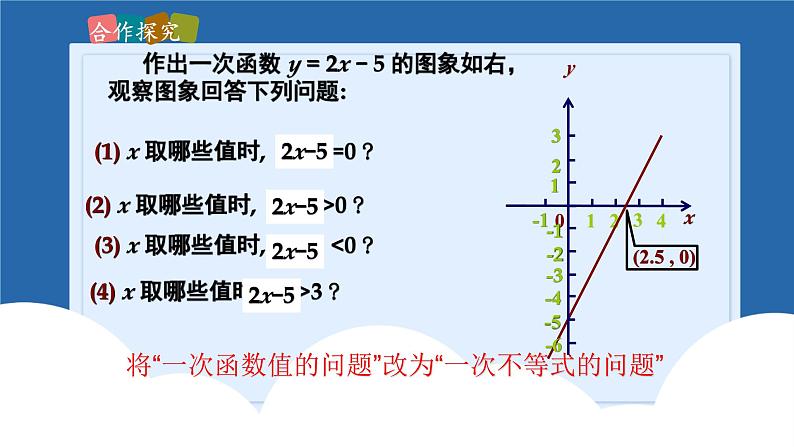
将“一次函数值的问题”改为“一次不等式的问题”
作出一次函数 y = 2x - 5 的图象如右，
(1) x 取哪些值时, y =0 ?
(2) x 取哪些值时, y >0 ?
(3) x 取哪些值时, y <0 ?
(4) x 取哪些值时, y >3 ?
因为 y = 2x – 5，
所以，将(1)～(4) 中的 y 换成 2x-5,中则原题“关于一次函数值的问题”转换成关于一次不等式的问题”。
我们既可以运用函数图象解不等式 ，也可以运用解不等式帮助研究函数问题 ，二者相互渗透 ，互相作用。
例 根据下列一次函数的图像，直接写出下列不等式的解集
(3) –x+3 ≥0
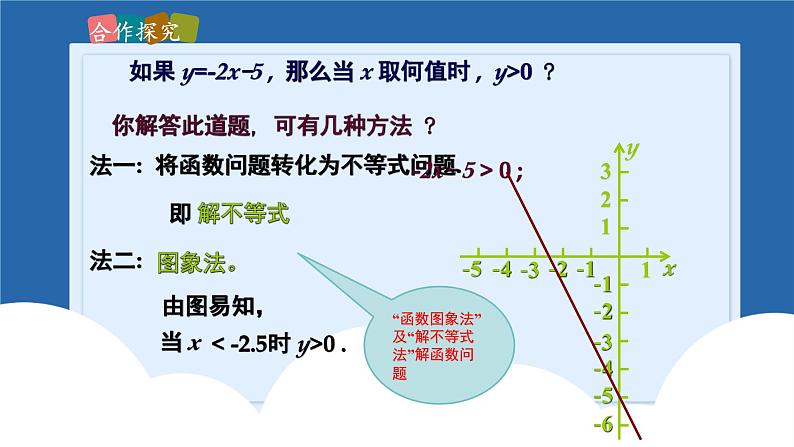
如果 y=-2x-5 , 那么当 x 取何值时 , y>0 ?
你解答此道题, 可有几种方法 ?
将函数问题转化为不等式问题.
-2x- 5 > 0 ;
< -2.5时 y>0 .
“函数图象法”及“解不等式法”解函数问题
如图，函数y＝kx＋b(k≠0)的图象经过点B(2,0)，与函数y＝2x的图象交于点A，则不等式0＜kx＋b＜2x的解集为
把A(x,2)代入y＝2x，得2x＝2，解得x＝1.∴点A的坐标为(1,2)，∴当x＞1时，2x＞kx＋b.又∵函数y＝kx＋b(k≠0)的图象经过点B(2,0)，∴不等式0＜kx＋b＜2x的解集为1＜x＜2.答案：1＜x＜2
如图所示，一次函数y1＝kx＋4与y2＝x＋b的图象交于点A．则下列结论中错误的是(　　)A．k＜0，b＞0B．2k＋4＝2＋bC．y1＝kx＋4的图象与y轴交于点(0,4)D．当x＜2时，y1>y2
若一次函数y＝kx＋b(k、b为常数，且k≠0)的图象经过点A(0，－1)、B(1,1)，则不等式kx＋b＞1的解为(　　)A．x＜0　B．x＞0　C．x＜1　D．x＞1
4．在一次函数y＝kx＋b中，当x＜－3时，y＞0；当x＞－3时，y＜0，则y＝kx＋b的图象与x轴的交点坐标为(　　)A．(3,0)　B．(0,0)　C．(－3,0)　D．无法确定
已知一次函数y＝kx＋b的图象如图所示，则关于x的不等式3kx－b＞0的解集为__________.
如图，已知一次函数y1＝2x＋b和y2＝ax－3的图象交于点P(－2，－5)，这两个函数的图象与x轴分别交于点A、B．(1)分别求出这两个函数的解析式；(2)求△ABP的面积；(3)根据图象直接写出不等式2x＋b＜ax－3的解集
解：(1)将点P(－2，－5)代入y1＝2x＋b，解得b＝－1.将点P(－2，－5)代入y2＝ax－3，解得a＝1.∴这两个函数的解析式分别为y1＝2x－1，y2＝x－3.　
(3)由函数图象，可知不等式2x＋b＜ax－3的解集为x<－2.