课件北师大版八年级下数学第二章一元一次不等式与一元一次不等式组2.7一元一次不等式与一元一次不等式组回顾与思考

这是一份课件北师大版八年级下数学第二章一元一次不等式与一元一次不等式组2.7一元一次不等式与一元一次不等式组回顾与思考，共23页。

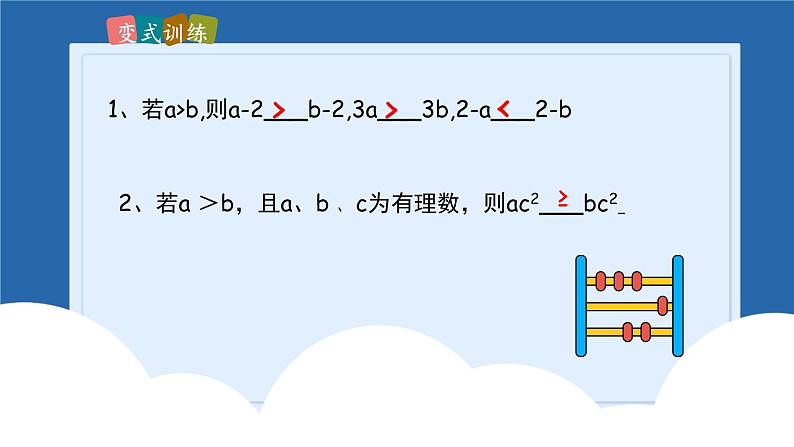
2021/6/301北师大版 八年级 数学 下册一元一次不等式与一元一次不等式组回顾与思考1、掌握不等式（组）的基本性质。2、会解一元一次不等式（组），并会用数轴表示不等式（组）的解集。3、会用一元一次不等式（组） 解决实际问题。考点一：不等式有关概念及基本性质不等式:表示不相等关系的式子叫做不等式.不等式的解:在含有未知数的不等式中,能使不等式成立的未知数的值叫做这个不等式的解. 不等式的解集:一个含有未知数的不等式的解的全体叫做这个不等式的解集.解不等式:求不等式解集的过程. 一元一次不等式:在不等式里,只含有一个未知数且未知数的次数是一次的不等式叫做一元一次不等式. 一元一次不等式组:关于同一个未知数的几个一元一次不等式合在一起，就组成一个一元一次不等式组。不等式性质(一)：不等式的两边都加上（或都减去）同一个整式，不等号的方向不变。不等式性质(二)不等式的两边都乘以（或都除以）同一个正数，不等号的方向不变。不等式的两边都乘以（或都除以）同一个负数，不等号的方向要改变。不等式性质(三)：考点一：不等式有关概念及基本性质5 不等式:用不等号连接起来的式子.用适当的符号表示下列关系:(1)a的2倍比8小(2)y的3倍与1的和大于3(3)x除以2的商加2至多为5(4)a与b两数和的平方不大于2 (5)x与y的差为非正数(6)a与4的和不小于22a＜83y+1＞3(a+b)2≤2X-y≤0a+4≥22、若a ＞b，且a、b 、 c为有理数，则ac2___bc2 ≥1、若a>b,则a-2___b-2,3a___3b,2-a___2-b>><7 解一元一次不等式步骤： 去分母 去括号 移项 合并同类项 系数化为1. 在系数化为1的这一步中,要特别注意不等式的两边都乘以(或除以)一个负数时,不等号的方向必须改变方向.一元一次不等式的解法8 8x-4≥15x-608x-15x≥-60+4 -7x≥-56 x≤8去分母得:去括号得:移项得:合并同类项得:化系数为1得:解:同除以-7,方向改变2021/6/309解：由 ，得102求不等式 3x+1≥4x-5的正整数解．移项得:合并同类项得:化系数为1得:解:3x﹣4x≥-5-1﹣x ≥-6x≤6所以不等式 的正整数解为：1、2、3、4、5、6(1)同大取最大，如；(2)同小取最小，如；(3)大小小大中间找，如:(4)大大小小找不了，如：X>-3X>-1X>-1X<1x<3X<1。0000-1-2-31231212考点二：一元一次不等式组><><1＜x＜2 无解121：解不等式组: 由不等式①得: x≤8由不等式②得: x≥5∴ 原不等式组的解集为:5≤x≤8解:①②132.求不等式组 的整数解.解:04不等式组的整数解为：3、4①②14不等式(组)在实际生活中的应用 当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.15列一元一次不等式组解应用题的一般步骤：1、审：审清题意，弄懂已知什么，求什么，以及各个数量之间的关系。2、设：只能设一个未知数，一般是与所求问题有直接关系的量。3、找：找出题中所有的不等关系，特别是隐含的数量关系。4、列：列出不等式组。5、解：分别解出每个不等式的解集，再求其公共部分，得出结果。6、答：根据所得结果作出回答。16例、某饮料厂为了开发新产品，用A、B两种果汁原料各19千克、17.2千克试制甲、乙两种新型饮料共50千克，下表是相关数据：(1)假设甲种饮料需配制x千克,请你写出满足题意的不等式组,并求出其解集.(2)若甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,设这两种饮料的成本总额为y元,请写出y与x的函数关系式(不要求写自变量的取值范围),并根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种饮料的成本总额最少？17解不等式组，得解：（1）由题意得：28≤x≤30（2）y=4x+3(50-x)，即y=x+150。因为x越小，y越小，所以当x=28时，y最小。即当甲种饮料配制28千克时，甲、乙两种饮料的成本总额最少。 某服装店欲购甲、乙两种新款运动服，甲款每套进价350元，乙款每套进价200元，该店计划用不低于7600元且不高于8000元的资金订购30套甲、乙两款运动服。 (1) 该店订购这两款运动服，共有哪几种方案？ (2) 若该店以甲款每套400元，乙款每套300元的价格全部出售，哪种方案获利最大？解： 设该店订购甲款运动服x套，则订购 乙款运动服(30-x)套，由题意，得 解这个不等式组，得∵x为整数，∴x取11，12、13∴30-x取19，18，17。 故该店订购这两款运动服，共有3种方案。 方案一：甲款11套，乙款19套 方案二：甲款12套，乙款18套； 方案三：甲款13套，乙款17套。  (2) 解法一： 设该店全部出售甲、乙两款运动服后获利y元，则 y=(400-350)x+(300-200)(30-x) =50x+3000-100x= -50x+3000，∵-50<0，∴y随x的增大而减小，∴当x=11时，y最大。 ∴ 方案一即甲款11套，乙款19套时，获利最大。 解法二： 三种方案分别获利为： 方案一：(400-350)´11+(300-200)´19=2450(元)。 方案二：(400-350)´12+(300-200)´18=2400(元)。 方案三：(400-350)´13+(300-200)´17=2350(元)。 ∵2450>2400>2350， ∴方案一即甲款11套，乙款19套，获利最大。 21A市有某种型号的农用车50辆，B市有40辆，现要将这些农用车全部调往C、D两县，C县需要该种农用车42辆，D县需要48辆，从A市运往C、D两县农用车的费用分别为每辆300元和150元，从B市运往C、D两县农用车的费用分别为每辆200元和250元．（1）设从A市运往C县的农用车为x辆，此次调运总费为y元，求y与x的函数关系式，并写出自变量x的取值范围；（2）若此次调运的总费用不超过16000元，有哪几种调运方案？哪种方案的费用最小？并求出最小费用？22解：（1）从A市运往C县的农用车为x辆，此次调运总费为y元，根据题意得：y=300x+200（42﹣x）+150（50﹣x）+250（x﹣2），即y=200x+15400，所以y与x的函数关系式为：y=200x+15400．又∵解得：2≤x≤42，且x为整数，所以自变量x的取值范围为：2≤x≤42，且x为整数．23（2）∵此次调运的总费用不超过16000元，∴200x+15400≤16000解得：x≤3，∴x可以取：2或3，方案一：从A市运往C县的农用车为2辆，从B市运往C县的农用车为40辆，从A市运往D县的农用车为48辆，从B市运往D县的农用车为0辆，方案二：从A市运往C县的农用车为3辆，从B市运往C县的农用车为39辆，从A市运往D县的农用车为47辆，从B市运往D县的农用车为1辆，当x=2时，y=200×2+15400=15800，当x=3时，y=200×3+15400=16000，所以∴当x=2时，y最小，即方案一费用最小，最小费用为15800元．