课件北师大版八年级第六章平行四边形北师大版八年级下册数学：平行四边形回顾与思考

这是一份课件北师大版八年级第六章平行四边形北师大版八年级下册数学：平行四边形回顾与思考，共39页。

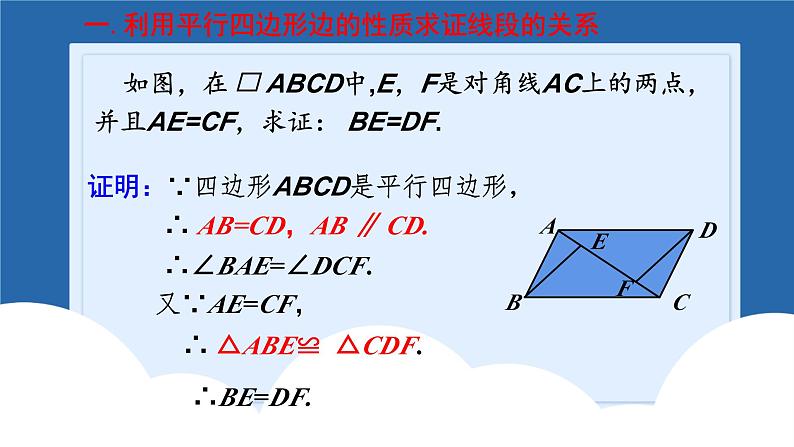
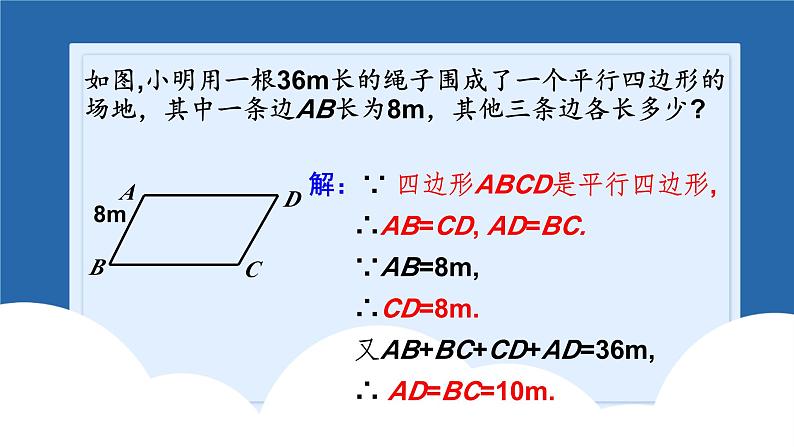
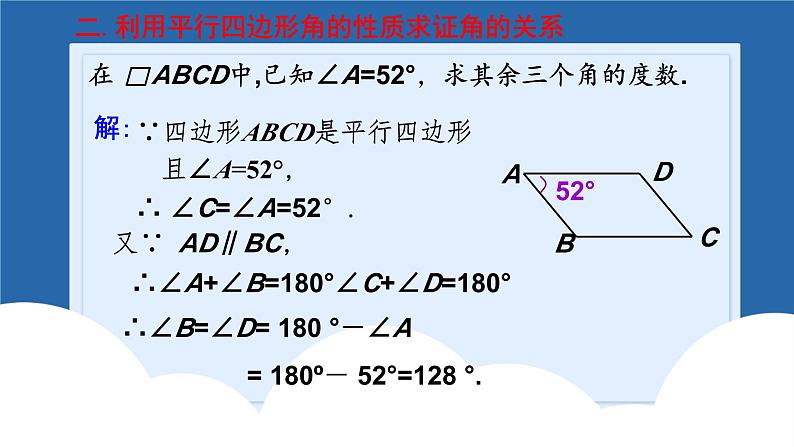
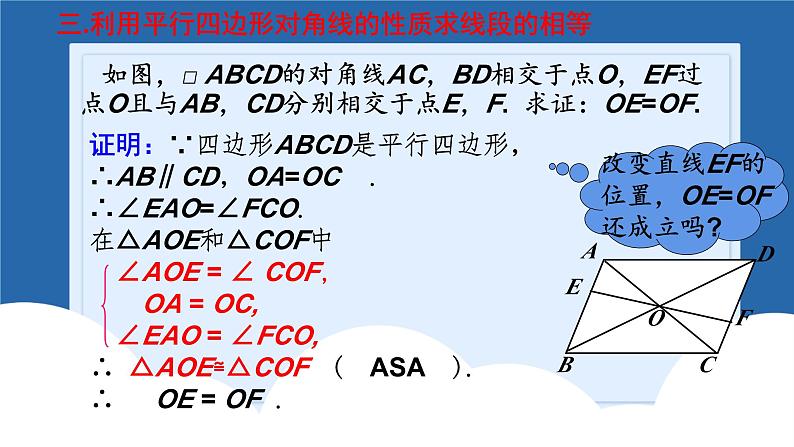
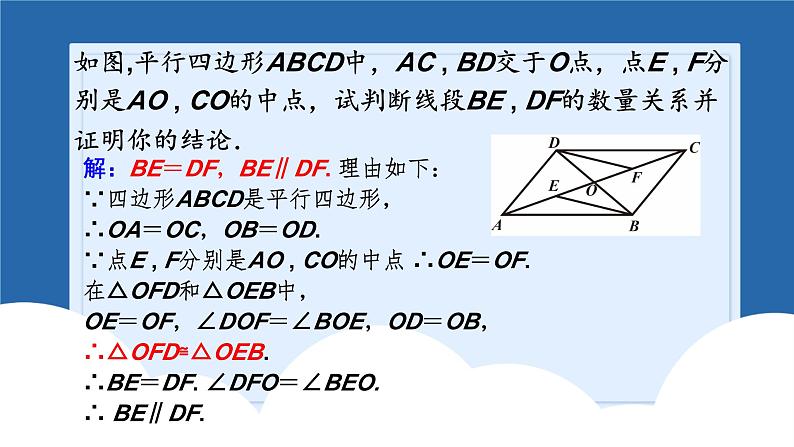
平行四边形回顾与思考2.平行四边形的对边平行且相等.3.平行四边形的对角相等.4.平行四边形的对角线互相平分.知识点一：性质1.平行四边形是中心对称图形，两条对角线的交点是它的对称中心证明：∵四边形ABCD是平行四边形，∴∠BAE=∠DCF.∴ △ABE≌ △CDF.∴ AB=CD，AB ∥ CD.又∵AE=CF，∴BE=DF. 一.利用平行四边形边的性质求证线段的关系如图,小明用一根36m长的绳子围成了一个平行四边形的场地，其中一条边AB长为8m，其他三条边各长多少? 解：∵ 四边形ABCD是平行四边形, ∴AB=CD, AD=BC. ∵AB=8m, ∴CD=8m. 又AB+BC+CD+AD=36m, ∴ AD=BC=10m.8m解:∴ ∠C=∠A=52°.又∵ AD∥BC,∴∠A+∠B=180°∠C+∠D=180°∴∠B=∠D= 180 °－∠A = 180º－ 52°=128 °.二.利用平行四边形角的性质求证角的关系 如图，□ ABCD的对角线AC，BD相交于点O，EF过点O且与AB，CD分别相交于点E，F. 求证：OE=OF.三.利用平行四边形对角线的性质求线段的相等证明：∵四边形ABCD是平行四边形，∴AB∥CD，OA=OC .∴∠EAO=∠FCO.在△AOE和△COF中 ∠AOE = ∠ COF, OA = OC, ∠EAO = ∠FCO,∴ △AOE≌△COF ( ASA ).∴ OE = OF .如图,平行四边形ABCD中，AC , BD交于O点，点E , F分别是AO , CO的中点，试判断线段BE , DF的数量关系并证明你的结论．解：BE＝DF，BE∥DF. 理由如下：∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD.∵点E , F分别是AO , CO的中点 ∴OE＝OF.在△OFD和△OEB中，OE＝OF，∠DOF＝∠BOE，OD＝OB， ∴△OFD≌△OEB.∴BE＝DF. ∠DFO＝∠BEO.∴ BE∥DF.1.两组对边分别平行的四边形是平行四边形.2.一组对边平行且相等的四边形是平行四边形.3.两组对边分别相等的四边形是平行四边形.4.对角线互相平分的四边形是平行四边形.知识点二：判定 如图，在Rt△MON中，∠MON＝90°.求证：四边形PONM是平行四边形．证明：在Rt△MON中，由勾股定理得(x－5)2＋42＝(x－3)2， 解得x＝8.∴PM＝11－x＝3，ON＝x－5＝3，MN＝x－3＝5.∴PM＝ON，OP＝MN，∴四边形PONM是平行四边形．一.利用两组对边分别相等识别平行四边形如图, AD⊥AC,BC⊥AC,且AB=CD,求证：四边形ABCD是平行四边形.证明：在Rt△ABC和Rt△CDA中，∵AC=CA,AB=CD,∴Rt△ABC≌Rt△CDA(HL).∴BC=DA.又∵AB=CD,∴四边形ABCD是平行四边形．如图，已知E，F，G，H分别是▱ABCD的边AB，BC，CD，DA上的点，且AE=CG，BF=DH．求证：四边形EFGH是平行四边形． 在平行四边形ABCD中，∠A=∠C，AD=BC,又∵BF=DH，∴AH=CF.又∵AE=CG，∴△AEH≌△CGF（SAS）.∴EH=GF.同理得△BEF≌△DGH（SAS）.∴GH=EF.∴四边形EFGH是平行四边形．证明： ∵四边形ABCD是平行四边形，∴AB =CD，EB //FD．又 ∵EB = AB ，FD = CD，∴EB =FD ．∴四边形EBFD是平行四边形． 如图 ，在平行四边形ABCD中，E，F分别是AB，CD的中点.求证：四边形EBFD是平行四边形. 二.直接利用一组对边平行且相等判定平行四边形证明：证明：∵四边形AEFD和EBCF都是平行四边形，∴AD∥ EF，AD=EF， EF∥ BC， EF=BC.∴AD∥ BC，AD=BC.∴四边形ABCD是平行四边形.四边形AEFD和EBCF都是平行四边形，求证：四边形ABCD 是平行四边形. 如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，AE=DF，∠A=∠D，AB=DC．求证：四边形BFCE是平行四边形． ∵AB=CD，∴AB+BC=CD+BC，即AC=BD，在△ACE和△DBF中， AC＝DB ,∠A＝∠D, AE＝DF ,∴△ACE≌△DBF(SAS).∴CE=BF，∠ACE=∠DBF.∴CE∥BF.∴四边形BFCE是平行四边形．证明：如图，点C是AB的中点，AD=CE，CD=BE．（1）求证：△ACD≌△CBE.（2）求证：四边形CBED是平行四边形．  如图， □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形. 证明：∵四边形ABCD是平行四边形，∴ AO=CO,BO=DO.∵AE=CF ，∴ AO-AE=CO-CF,即EO=OF.又∵BO=DO，∴四边形BFDE是平行四边形.三利用平行四边形的判定定理3判定平行四边形如图，AC∥DE且AC＝DE，AD，CE交于点B，AF，DG分别是△ABC，△BDE的中线，求证：四边形AGDF是平行四边形. ∵AC∥DE，AC＝DE，∴∠C＝∠E，∠CAB＝∠EDB.∴△ABC≌△DBE.∴AB＝DB，CB＝EB.∵AF，DG分别是△ABC，△BDE的中线，∴BG＝BF.∴四边形AGDF是平行四边形.证明：如图, AD⊥AC,BC⊥AC,且AB=CD,求证：四边形ABCD是平行四边形.证明：在Rt△ABC和Rt△CDA中，∵AC=CA,AB=CD,∴Rt△ABC≌Rt△CDA(HL).∴BC=DA.又∵AB=CD,∴四边形ABCD是平行四边形．已知：四边形ABCD, ∠A=∠C，∠B=∠D.求证：四边形ABCD是平行四边形.证明：∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).同理可证AB∥CD.又∵∠A+ ∠B+ ∠C+ ∠D =360 °,∴ 2∠A+ 2∠B=360 °,∵∠A=∠C，∠B=∠D（已知）,即∠A+ ∠B=180 °.∴ AD∥BC （同旁内角互补，两直线平行）. 如图，△ABC中，BD平分∠ABC，DF∥BC，EF∥AC，试问BF与CE相等吗？为什么？平行四边形的性质和判定的综合题目解：BF＝CE．理由如下：∵DF∥BC，EF∥AC，∴四边形FECD是平行四边形，∠FDB=∠DBE.∴FD=CE.∵BD平分∠ABC，∴∠FBD=∠EBD.∴∠FBD=∠FDB.∴BF=FD.∴BF＝CE.知识点三：平行线之间的距离如果两条直线互相平行，则其中一条直线上任意一点到另一条直线的距离相等，这个距离成为平行线之间的距离.平行线之间的距离处处相等如图，AB∥CD，BC⊥AB，若AB=4cm，S△ABC=12cm2，求△ABD中AB边上的高．解：∵S△ABC = AB•BC, = ×4 ×BC=12cm2， ∴BC=6cm. ∵AB∥CD， ∴点D到AB边的距离等于BC的长度， ∴△ABD中AB边上的高为6cm.总结：平行四边形的对角线分平行四边形为四个面积相等的三角形，且都等于平行四边形面积的四分之一.相对的两个三角形全等.知识点四：平行四边形面积问题 如图，AC,BD交于点O，EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗？MN解：设直线EF交AD,BC于点N,M.∵AD∥BC,∴∠NAO=∠MCO,∠ANO=∠CMO.又∵AO=CO,∴△NAO≌△MCO，∴S四边形ANMB=S△NAO+S△AOB+S△MOB=S△MCO+S△AOB+S△MOB =S△AOB+S△COB= .∴S四边形ANMB=S四边形CMND,即平行四边形ABCD被EF所分的两个四边形面积相等.如图，平行四边形ABCD中，DE⊥AB于E，DF⊥BC于F，若平行四边形ABCD的周长为48，DE=5，DF=10，求平行四边形ABCD的面积.解：设AB=x，则BC=24-x.根据平行四边形的面积公式可得,5x=10(24-x)，解得x=16．则平行四边形ABCD的面积为5×16=80．如图，在四边形ABCD中，AD∥BC，AD=12cm，BC=15cm，点P自点A向D以1cm/s的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，点P，Q同时出发，设运动时间为t(s)．（1）用含t的代数式表示： AP=_____； DP=________； BQ=________；CQ=________；tcm(12-t)cm(15-2t)cm2tcm（2）当t为何值时，四边形APQB是平行四边形？解：根据题意有AP=tcm，CQ=2tcm，PD=(12-t)cm，BQ=(15-2t)cm．∵AD∥BC，∴当AP=BQ时，四边形APQB是平行四边形．∴t=15-2t，解得t=5．∴t=5时四边形APQB是平行四边形.解：由PD=(12-t)cm，CQ=2tcm，∵AD∥BC，∴当PD=QC时，四边形PDCQ是平行四边形．即12-t=2t，解得t=4s，∴当t=4s时，四边形PDCQ是平行四边形．（3）当t为何值时，四边形PDCQ是平行四边形？知识点六：中位线定义：连结三角形两边中点的线段叫做三角形的中位线性质：三角形的中位线平行于第三边并且等于第三边的一半. 如图，在△ABC中，D,E分别为AC,BC的中点，AF平分∠CAB，交DE于点F.若DF＝3，求AC的长.解：∵D,E分别为AC,BC的中点，∴DE∥AB，∴∠2＝∠3.又∵AF平分∠CAB，∴∠1＝∠3.∴∠1＝∠2.∴AD＝DF＝3.∴AC＝2AD＝2DF＝6. 如图，D,E分别是△ABC的边AB,AC的中点，点O是△ABC内部任意一点，连接OB,OC，点G,F分别是OB,OC的中点，顺次连接点D,G,F,E.求证：四边形DGFE是平行四边形.∴四边形DGFE是平行四边形.证明：在△ABC中，∵AD=BD,AE=CE,在△OBC中，∵OG=BG,OF=CF,已知: 如图,点E,F,G,H分别是四边形ABCD各边中点，求证：四边形EFGH为平行四边形.证明：连接AC.∵ E , F是AB , BC边中点,∴EF∥AC且EF＝ AC.同理：HG ∥ AC且HG ＝ AC.∴EF ∥ HG且EF ＝ HG.∴四边形EFGH为平行四边形.EFGHABCD 如图，在四边形ABCD中，AB=CD，M ，N ， P分别是AD ， BC，BD的中点，∠ABD=20°，∠BDC=70°，求∠PMN的度数．解：∵M,N,P分别是AD,BC,BD的中点，∴PN，PM分别是△CDB与△DAB的中位线.∴PM= AB，PN= DC，PM∥AB，PN∥DC.∵AB=CD，∴PM=PN.∴△PMN是等腰三角形.∵PM∥AB，PN∥DC，∴∠MPD=∠ABD=20°，∠BPN=∠BDC=70°.∴∠MPN=∠MPD+(180°−∠NPB)=130°.∴∠PMN=(180°−130°)÷ 2 =25°．知识点七：多边形内角和和外角和 多边形外角和都等于360° 1 若正多边形的一个内角是150°，则该正多边形的边数是（ ）.A.6 B.12 C.16 D.18【分析】 设多边形的边数为n.根据题意，得 （n-2) ·180°= 150°· n 解得n=12B2、求正十二边形的每个内角和每个外角的度数？解：正十二边形的每个内角的度数为 (12-2)×180°=150°每个外角的度数为=30°12 3、一个多边形，每一个外角都等于45°，这个多边形是几边形，它的内角和是多少？解：∵ 多边形的外角和是360°，360°÷45°∴ 多边形的边数为=8∴ 这个多边形的内角和为(8-2)×180°=1080°且每一个外角都等于45°注意：正多边形的边数=360°÷一个外角的度数 在各个内角都相等的多边形中，一个外角等于一个内角的 ，求这个多边形的每一个内角的度数和它的边数. 则其每个外角的度数为 x° .解：设这个多边形的每一个内角的度数为x°，根据题意，得x°+ x°=180°解的x=144180°÷144°∴ 多边形的一个外角的度数为=36°360°÷36°∴ 多边形的边数为=10如图，五边形ABCDE是正五边形，连接BD , CE，交于点P． 求证：四边形ABPE是平行四边形．证明：∵五边形ABCDE是正五边形，∴正五边形的每个内角的度数是 AB=BC=CD=DE=AE.∴∠DEC=∠DCE= ×(180°-108°)=36°，同理∠CBD=∠CDB=36°，∴∠ABP=∠AEP=108°-36°=72°.∴∠BPE=360°-108°-72°-72°=108°=∠A.∴四边形ABPE是平行四边形．