初中1 用相同的正多边形优秀课件ppt

这是一份初中1 用相同的正多边形优秀课件ppt，文件包含931用相同的正多边形铺设地面pptx、931用相同的正多边形铺设地面教学设计doc、931用相同的正多边形铺设地面学案doc等3份课件配套教学资源，其中PPT共24页， 欢迎下载使用。
n边形的内角和公式是什么？n边形的外角和是多少度？
n边形的内角和为(n -2) ·180°外角和是360°
某些形状的地砖或瓷砖为什么能铺满地面而不留一点空隙?实际生活中,它们的形状大多是正多边形,就让我们从此开始,探究一下其中的奥秘吧!
使用给定的某种正多边形,它能否铺满地面,既不留下一丝空白,又不相互重叠呢?
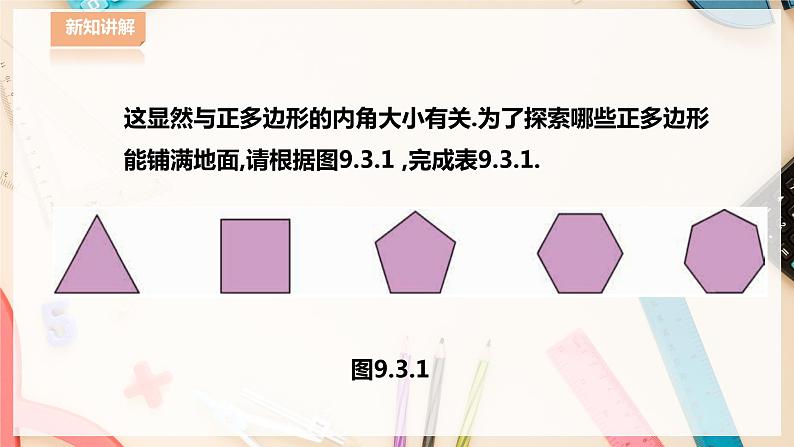
这显然与正多边形的内角大小有关.为了探索哪些正多边形能铺满地面,请根据图9.3.1 ,完成表
(n-2) · 180°
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
如正六边形的每个内角为120°,三个120°拼在一起恰好组成周角,所以全用正六边形瓷砖就可以铺满地面(如图9.1.1(3)所示).
参见图9.1.1(1)、(2),你能说明为什么正三角形和正方形能铺满地面吗?
正三角形的每个内角为60°,6个60°拼在一起恰好组成周角,所以全用正三角形瓷砖就可以铺满地面。
正方形的每个内角为90°,四个90°拼在一起恰好组成周角,所以全用正方形瓷砖就可以铺满地面。
如图9.3.2,正五边形不能铺满地面,正八边形也不能铺满地面.
规律总结：围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
1、 下列正多边形地砖中，用同一种正多边形地砖不能铺满地面的是（ ）    A. 正三角形B. 正四边形C. 正六边形D. 正八边形
解：A.正三角形的每个内角是60°，能整除360°，能密铺，故不符合题意B.正四边形的每个内角是90°，能整除360°，能密铺，故不符合题意C.正六边形的每个内角是120°，能整除360°，能密铺，故不符合题意D.正八边形的每个内角是135°，不能整除360°，不能密铺，故符合题意故选D．
2、我们知道正五边形不能进行平面镶嵌，若将三个完全相同的正五边形按如图所示的方式拼接在一起，那么图中∠1的度数是（ ）A. 18° B. 30°C. 36°D. 54°
解：正五边形的每个内角为（5-2）×180°÷5=108°，∠1=360°-108°×3=36°，故选C．
3、如图所示的地面全是用正三角形的材料铺设而成的．（1）用这种形状的材料为什么能铺成平整、无隙的地面？（2）像这样铺设地面，能否全用正十边形的材料？为什么？
解：（1）每个顶点周围有6个正三角形的内角，恰好可以组成一个周角．  （2）不能． 理由：因为正十边形的任意几个内角都不能组成一个周角，所以不能全用正十边形的材料．
4、已知一个正多边形的内角的度数比与其相邻的外角的度数大140°．（1）求这个正多边形的内角与外角的度数（2）直接写出这个正多边形的边数（3）只用这个正多边形若干个，能否镶嵌并说明理由．
解：(1)正多边形的内角的度数为160°，外角的度数为20°(2)18(3)不能. 理由: ∵正多边形的内角为160°，不能整除360°， ∴不能镶嵌.
用相同的正多边形铺设地面
围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面.
9.3.1 用相同的正多边形铺设地面
1、规律总结 2、练习题