初中数学华师大版七年级下册7.4 实践与探索优秀ppt课件

这是一份初中数学华师大版七年级下册7.4 实践与探索优秀ppt课件，文件包含74实践与探索pptx、74实践与探索教学设计doc、74实践与探索学案doc等3份课件配套教学资源，其中PPT共29页， 欢迎下载使用。

解一元一次方程的应用题步骤是？
审，认真审题，找数量关系设，设未知数，列，列一元一次方程解，解方程验，检验答案是否符合题意答，解答
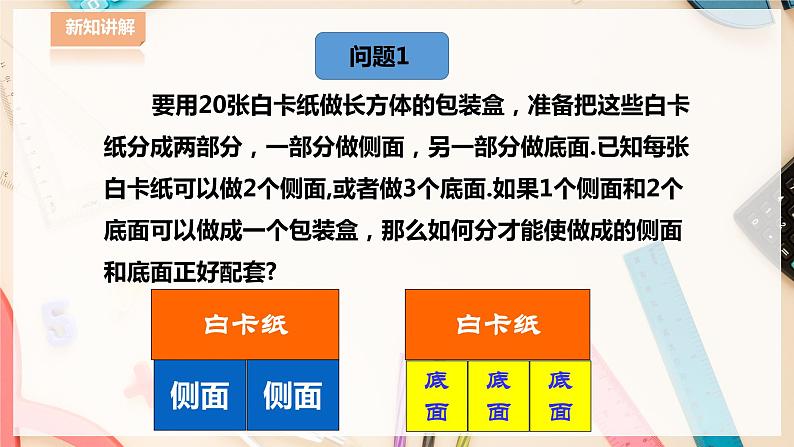
要用20张白卡纸做长方体的包装盒，准备把这些白卡纸分成两部分，一部分做侧面，另一部分做底面.已知每张白卡纸可以做2个侧面,或者做3个底面.如果1个侧面和2个底面可以做成一个包装盒，那么如何分才能使做成的侧面和底面正好配套?
请你设计一种分法.想一想,如果可以将一张白卡纸裁出一个侧面和一个底面,那么,该如何分这些白卡纸，才能既使做出的侧面和底面配套，又能充分利用白卡纸?
1.本题中的已知量(1)共有白卡纸20张。(2)一张白卡纸可以做2个侧面或3个底面。(3)1个侧面与2个底面配成一套。2.从已知中找出两个等量关系.(1)用做侧面的白卡纸张数+用做底面的白卡纸张数=20(2)底面的个数是侧面的个数的2倍3.本题求的量 用几张白卡纸做侧面，几张白卡纸做底面，侧面与底面刚好配套。
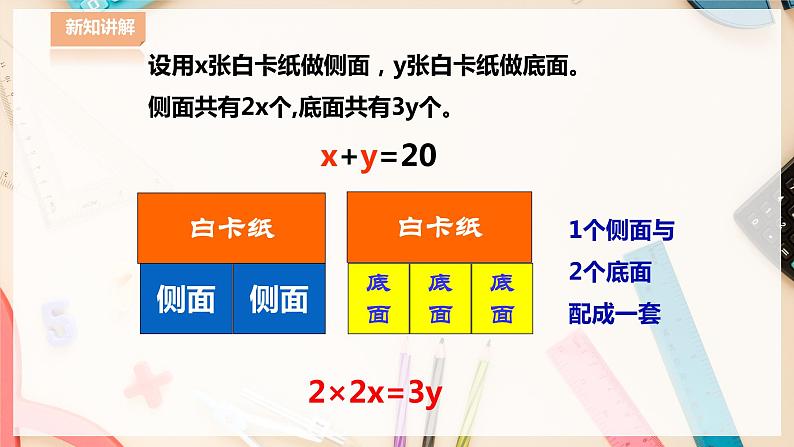
设用x张白卡纸做侧面，y张白卡纸做底面。侧面共有2x个,底面共有3y个。x+y=20
1个侧面与2个底面配成一套
解：设用x张白卡纸做侧面，y张白卡纸做底面。依题意得解方程组得当白卡纸可以套裁时,用8张做侧面,11张做底面，另一张套裁出1个侧面,1个底面,则共可做盒身17个,盒底盖34个,正好配成17个包装盒,充分利用了材料。
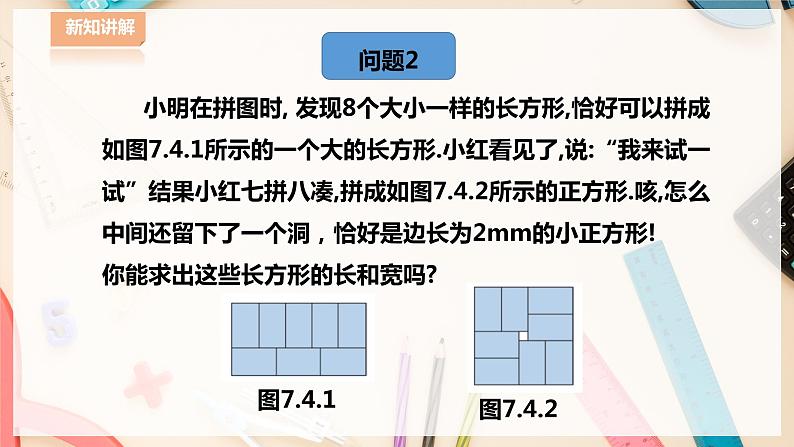
小明在拼图时, 发现8个大小一样的长方形,恰好可以拼成如图7.4.1所示的一个大的长方形.小红看见了,说:“我来试一试”结果小红七拼八凑,拼成如图7.4.2所示的正方形.咳,怎么中间还留下了一个洞，恰好是边长为2mm的小正方形!你能求出这些长方形的长和宽吗?
设长方形的长和宽分别为x mm、y mm.图7.4.2给我们提供了一个信息:S大正方形-8xS长方形=22,即(x +2y)2-8xy=4.但这是我们还没有研究过的方程!你有什么其他办法来解决这个问题?
一条路不通，另辟蹊径!仔细观察两幅图,你还能发现哪些有用的信息?
1.从第一个拼图中，能否得出小长方形的长xmm与宽ymm之间的一种等量关系？2.从第二个拼图中，能否得到x、y之间另一种等量关系呢？
3.列出方程（组）,并求解.设长方形的长为xmm,宽为ymm.解得答：长方形的长为10mm,宽为6mm.
在6.3节提出的问题中选出一个，用本章的方法来处理，并比较一下两种方法，谈谈你的感受.
6.3问题1（2）用一根长60厘米的铁丝围成一个长方形.(2)如果长方形的宽比长少4厘米,求这个长方形的面积;
解：设长方形长为x厘米，宽为y厘米。解得长方形长为17厘米，宽为13厘米，S＝13×17＝221(平方厘米)。
列二元一次方程组解应用题的步骤：1.审题:分析题目中已知量和未知量；2.设未知数：设未知数，一般设为x，y (要注意单位)；
3.找等量关系：找出等量关系；4.列方程组：根据等量关系列二元一次方程组；5.解方程组：解二元一次方程组；6.检验并作答：代入方程组，检验是否符合题意。
变式1 某加工厂有工人50名，生产某种一个螺栓套两个螺母的配套产品，每人每天平均生产螺栓14个或螺母20个，应分配多少人生产螺栓，多少人生产螺母，能使生产出的螺栓和螺母刚好配套？设应安排x人生产螺栓，y人生产螺母，则所列方程组为( )
解：生产螺栓的工人人数+生产螺母的工人人数=50；生产的螺栓的数量×2=生产的螺母的数量设生产螺栓的有x人，生产螺母的有y人．由题意，得 ,故选B
变式2 一块长方形菜园，长是宽的3倍，如果长减少3米，宽增加4米，这个长方形就变成一个正方形．设这个长方形菜园的长为x米，宽为y米，根据题意，得( )
解 根据等量关系：长是宽的3倍；长减少3m，宽增加4m，这个长方形就变成一个正方形这个长方形菜园的长为x米，宽为y米由题意得 故选C.
1、机械厂加工车间有85名工人，平均每人每天加工大齿轮16个或小齿轮10个，已知2个大齿轮与3个小齿轮配成一套，问需分别安排多少名工人加工大、小齿轮，才能使每天加工的大小齿轮刚好配套？设安排x名工人加工大齿轮，安排y名工人加工小齿轮，可列方程组为( )
解：设需安排x名工人加工大齿轮，y名工人加工小齿轮，根据题意可得 故选：B．
2、如图，周长为68cm的长方形ABCD被分成7个形状大小完全相同的小长方形，则长方形ABCD的面积为( )A. 40cm2 B. 128cm2 C. 280cm2 D. 140cm2
解：设小长方形的长为xcm，宽为ycm，依题意，得： 解得：∴2x (x+y)=280．
3、亚洲文明对话大会召开期间，大批的大学生志愿者参与服务工作．某大学计划组织本校全体志愿者统一乘车去会场，若单独调配36座新能源客车若干辆，则有2人没有座位；若只调配22座新能源客车，则用车数量将增加4辆，并空出2个座位．(1)计划调配36座新能源客车多少辆？该大学共有多少名志愿者？(2)若同时调配36座和22座两种车型，既保证每人有座，又保证每车不空座，则两种车型各需多少辆？
解：(1)设计划调配36座新能源客车x辆，该大学共有y名志愿者，则需调配22座新能源客车(x+4)辆，依题意，得： 解得：答：计划调配36座新能源客车6辆，该大学共有218名志愿者．
解：(2)设需调配36座客车m辆，22座客车n辆，依题意，得：36m+22n=218，∴n= 又∵m，n均为正整数，∴答：需调配36座客车3辆，22座客车5辆．
解二元一次方程组应用题步骤1.审题 2.设未知数 3.找等量关系 4.列方程组 5.解方程组 6.检验并作答.
问题1、问题2、解二元一次方程组应用题步骤