新疆乌鲁木齐市米东区四校联考2023届高三下学期3月月考数学（理）试卷(含答案)

这是一份新疆乌鲁木齐市米东区四校联考2023届高三下学期3月月考数学（理）试卷(含答案)，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题
1．若复数z满足,则( )
A.B.C.D.
2．下列说法错误的是( )
A.如果一组数据的众数是5,那么这组数据中出现次数最多的数是5
B.一组数据的平均数一定大于其中每一个数据
C.一组数据的平均数,众数,中位数有可能相同
D.一组数据的中位数有且只有一个
3．已知全集,集合,,则( )
A.B.C.D.
4．某同学过18岁生日时,订了一个三层的蛋糕.已知该蛋糕三层均为高相等的圆柱形,且自上而下,三层蛋糕的半径分别为7cm,10cm,14cm.若该蛋糕的总体积为3450,则所需要长方体包装盒的体积至少为( )
A.23520B.7840C.15880D.19280
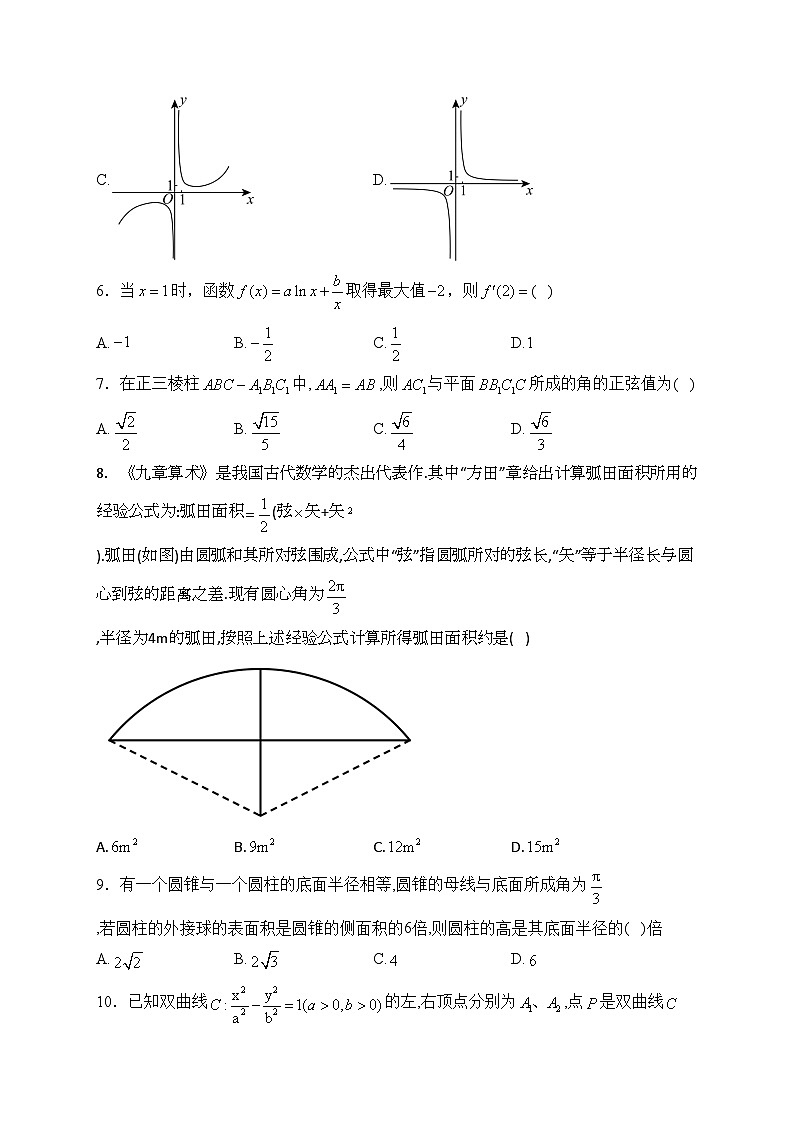
5．函数的图象大致是( )
A.B.
C.D.
6．当时，函数取得最大值，则( )
A.B.C.D.1
7．在正三棱柱中,,则与平面所成的角的正弦值为( )
A.B.C.D.
8．《九章算术》是我国古代数学的杰出代表作.其中“方田”章给出计算弧田面积所用的经验公式为:弧田面积(弦矢+矢).弧田(如图)由圆弧和其所对弦围成,公式中“弦”指圆弧所对的弦长,“矢”等于半径长与圆心到弦的距离之差.现有圆心角为,半径为4m的弧田,按照上述经验公式计算所得弧田面积约是( )
A.B.C.D.
9．有一个圆锥与一个圆柱的底面半径相等,圆锥的母线与底面所成角为,若圆柱的外接球的表面积是圆锥的侧面积的6倍,则圆柱的高是其底面半径的( )倍
A.B.C.D.
10．已知双曲线的左,右顶点分别为,点是双曲线上与不重合的动点,若,则双曲线的离心率为( )
A.B.C.4D.2
11．函数在上的最小值为,则的取值范围为( )
A.B.C.D.
12．已知函数的最大值为,则a等于( )
A.B.C.D.
二、填空题
13．如图,在边长为2的菱形ABCD中,E为CD中点,则__________,
14．已知点,,若圆与以线段AB为直径的圆相外切,则实数r的值是__________.
15．平面内有12个点,其中有4个点共线,此外再无任何3点共线,以这些点为顶点,可得_____个不同的三角形.
16．在中,,D为AC的中点,,则面积的最大值为______.
三、解答题
17．已知数列中,,且
（1）求证:数列是等差数列;
（2）令,求数列的前n项和.
18．如图,四棱锥的底面ABCD是正方形,PD垂直于底面ABCD,.
（1）若M是PC的中点,证明:平面PBC;
（2）求三棱锥的体积.
19．哈尔滨红肠已有近百年历史,是哈尔滨特产,也是黑龙江特产的代表,深受广大民众的喜爱,哈尔滨红肠是用大兴安岭的老果木熏制而成的,因此它除了肉香还会散发着浓郁的果木香.某调查机构从年龄在岁的游客中随机抽取100人,对是否有意向购买哈尔滨红肠进行调查,结果如下表:
（1）若以年龄40岁为分界线,由以上统计数据完成下面的2×2列联表,并判断是否有97.5%的把握认为购买哈尔滨红肠与人的年龄有关？
（2）用样本估计总体,用频率估计概率,从年龄在的所有游客中随机抽取3人,设这3人中打算购买哈尔滨红肠的人数为X,求X的分布列和数学期望.
参考数据:,其中.
20．已知抛物线上一点到焦点的距离为4,动直线交抛物线于坐标原点O和点A,交抛物线的准线于点B,若动点P满足,动点P的轨迹C的方程为.
（1）求出抛物线的标准方程;
（2）求动点P的轨迹方程;
（3）以下给出曲线C的四个方面的性质,请你选择其中的三个方面进行研究:
①对称性;
②范围;
③渐近线;
④时,写出由确定的函数的单调区间.
21．已知函数.
（1）判定函数的单调性;
（2）若,且,证明:.
22．已知点C是平面直角坐标系中异于原点O的一个动点,过点C且与y轴垂直的直线与直线交于点M,且向量与向量垂直.
（1）求点C的轨迹方程E;
（2）设C位于第一象限,以OC为直径的圆与y轴相交于点N,且,求的值.
23．已知x,y,z均为正实数,且.
证明:（1）;
（2）.
参考答案
1．答案：C
解析：因为,
所以,
所以.
故选:C
2．答案：B
解析：根据平均数,众数,中位数的概念可知,
如果一组数据的众数是5,那么这组数据中出现次数最多的数是5,故A正确;
一组数据的平均数不一定大于其中的每一个数,也可能相等,也可能小于,故B错误;
一组数据的平均数,众数,中位数有可能相同,故C正确;
一组数据的中位数有且只有一个,故D正确.
故选:B.
3．答案：B
解析：因为,又全集,
所以.
故选:B
4．答案：A
解析：设每层蛋糕的高为h,则蛋糕的体积,
解得,所以包装盒的高至少为,且底面至少为边长28cm的正方形,则包装盒的体积至少为.
故选:A
5．答案：C
解析：令函数,
,且,
函数为奇函数,故排除A;
,故排除B;
,,,故排除D.
故选:C.
6．答案：B
解析：因为函数定义域为，所以依题可知，，，而，所以，，即，，所以，因此函数在上递增，在上递减，时取最大值，满足题意，即有.
故选：B.
7．答案：C
解析：由题意可知底面三角形是正三角形,过A作于D,连接,则为所求,
,故选C.
8．答案：B
解析:依题意,弦(m),矢(m),
则弧田面积(),
所以弧田面积约是.
故选:B
9．答案：A
解析：设圆柱的高为h,底面半径为r,圆柱的外接球的半径为R,
则,
母线长,
圆锥的高为,圆锥的侧面积为,
,
,整理可得,
则.
故选:A
10．答案：D
解析：设,,,
,
,即,①
又,②,
由①②可得,
,
,
,
,
即,
故选D.
11．答案：C
解析：由关于原点对称可知,只需讨论函数函数与y轴最近的对称轴与,的关系即可.
当时,在y轴左边最近的对称轴为,,
此时,.
当时,在y轴右边边最近的对称轴为,,
此时,,因为故
故
故选:C
12．答案：B
解析：,
,
,
所以,,
由,可得,由,可得,
故在内单调递增,在内单调递减,
故当时,函数有最大值.
故选:B.
13．答案：
解析：将表示为,然后利用向量的运算法则及数量积的定义即可求解.
在菱形ABCD中,,所以三角形ABD是正三角形,从而,,
故答案为1.
14．答案：
解析：,,则,AB中点为:.
以线段AB为直径的圆圆心为,半径为.
圆C与以线段AB为直径的圆相外切,所以圆心距.
所以.
故答案为.
15．答案：216
解析：由题意,
故答案为216.
16．答案：
解析：设,,
由于,
在和中应用余弦定理可得:
,整理可得:,
结合勾股定理可得的面积:
,
当且仅当时等号成立.
则面积的最大值为.
故答案为:
17．答案：（1）见解析
（2）
解析：（1）因为数列中,,
所以,即;
因此,数列是以4为公差的等差数列;
（2）因为,所以,由（1）可得;
所以;
又数列的前n项和为,
所以①
则②
①②得,
整理得
18．答案：（1）证明见解析;
（2）.
解析：（1）平面ABCD,.
又ABCD是正方形,.
,平面PCD.
平面PCD,.
又,E是PC的中点,所以.
又,平面PBC.
（2）在平面PCD内过M作交CD于N,
所以且平面ABCD,
所以三棱锥的体积为
.
又三棱锥的体积等于三棱锥的体积,
三棱锥的体积等于.
19．答案：（1）列联表见解析,有97.5%的把握认为购买哈尔滨红肠与人的年龄有关.
（2）分布列见解析,.
解析：（1）由题可知,
的观测值,所以有97.5%的把握认为购买哈尔滨红肠与人的年龄有关.
（2）由题意可知,从年龄在的所有游客中随机抽取1人,打算购买哈尔滨红肠的概率为,所以,即,,1,2,3.
所以,,,,X的分布列为
.
20．答案：（1）;
（2）;
（3）见解析.
解析：（1）由题意,,所以
所以抛物线的标准方程为
（2）设,则与抛物线方程联立,可得,,即,与联立,可得.因为,所以,所以,,故,.
消去k可得
（3）由,可得
①因为,,故关于x轴对称;
②范围:,则.即
又当时,,
故,即或.
故,
③因为分母为,故渐近线
④当时,因为,所以由确定的函数为,即
,
当时,单调递减;当时,单调递增
故在上递减,在上递增.
综上所述,
①关于x轴对称
②,
③渐近线
④时,由确定的函数在上递减,在上递增
21．答案：（1）单调递增区间是,单调递减区间是;
（2）详见解析.
解析：（1）,,
当,,,,
单调递增区间是,单调递减区间是;
（2）令,则,
故在上是增函数,,故,
又,由得,
且在区间上,,,
若,则由在区间上递减得,
,,
若,则由,且在是增函数,
,,
化为.
综上可得.
22．答案：（1）;
（2）.
解析：（1）设,则,,,
,,
点C的轨迹方程
（2）由题意知:,,,
直线OC倾斜角为,则直线OC方程为,
由得:或,点C异于原点O,,
.
23．答案：（1）证明见解析;
（2）证明见解析.
解析：（1）由基本不等式,可得,,,
所以.
当且仅当时等号成立,即,
又由,所以.
（2）由题意知,
可得.
当且仅当时等号成立,所以.
年龄/岁
抽取人数
18
22
25
27
8
有意向购买红肠的人数
8
17
22
24
4
年龄低于40岁的人数
年龄不低于40岁的人数
总计
有意向购买哈尔滨红肠的人数
无意向购买哈尔滨红肠的人数
总计
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
年龄低于40岁的人数
年龄不低于40岁的人数
总计
有意向购买哈尔滨红肠的人数
25
50
75
无意向购买哈尔滨红肠的人数
15
10
25
总计
40
60
100
X
0
1
2
3
P