2022-2023学年广东省肇庆市高一（下）期末数学试卷（含详细答案解析）

这是一份2022-2023学年广东省肇庆市高一（下）期末数学试卷（含详细答案解析），共17页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
1.函数f(x)=sinxcsx的最小正周期为( )
A. 1B. 2C. πD. 2π
2.在△ABC中，角A、B、C的对边分别是a、b、c，若a= 2，b= 3，B=π3，那么角A等于( )
A. π4B. 3π4C. π4或3π4D. π6
3.已知向量a，b满足(a+b)⋅b=16，|b|=2，则a在b上的投影向量为( )
A. 3bB. 6bC. 9bD. 12b
4.已知向量a=(x+1,1)，b=(−8,x2+15)，在集合{0,1,2,3,4,5,6}中随机取值作为x，则a⊥b的概率为( )
A. 17B. 27C. 37D. 47
5.设z为复数，若(1+i)z>0，则z在复平面内对应的点位于( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
6.圆锥的母线l、高h、底面半径r满足l−h=h−r=1，则该圆锥的侧面积为( )
A. 10πB. 15πC. 20πD. 30π
7.已知三棱锥P−ABC的底面ABC为直角三角形，且∠ACB=π2.若PA⊥平面ABC，且AB=3，PA=4，三棱锥P−ABC的所有顶点均在球O的球面上，记球O的体积和表面积分别为V，S，则VS=( )
A. 512B. 56C. 53D. 52
8.给定一个正整数n(n≥3)，从集合Ω={1,2,3,⋯,n}中随机抽取一个数，记事件A=“这个数为偶数”，事件B=“这个数为3的倍数”.下列说法正确的是( )
A. 若n=6k，k∈N*，则至少存在一个n，使事件A和事件B不独立
B. 若n≠6k，k∈N*，k∈N*，则存在无穷多个n，使事件A和事件B独立
C. 若n为奇数，则至少存在一个n，使事件A和事件B独立
D. 若n为偶数，则对任意的n，事件A和事件B独立
二、多选题：本题共4小题，共20分。在每小题给出的选项中，有多项符合题目要求。全部选对的得5分，部分选对的得2分，有选错的得0分。
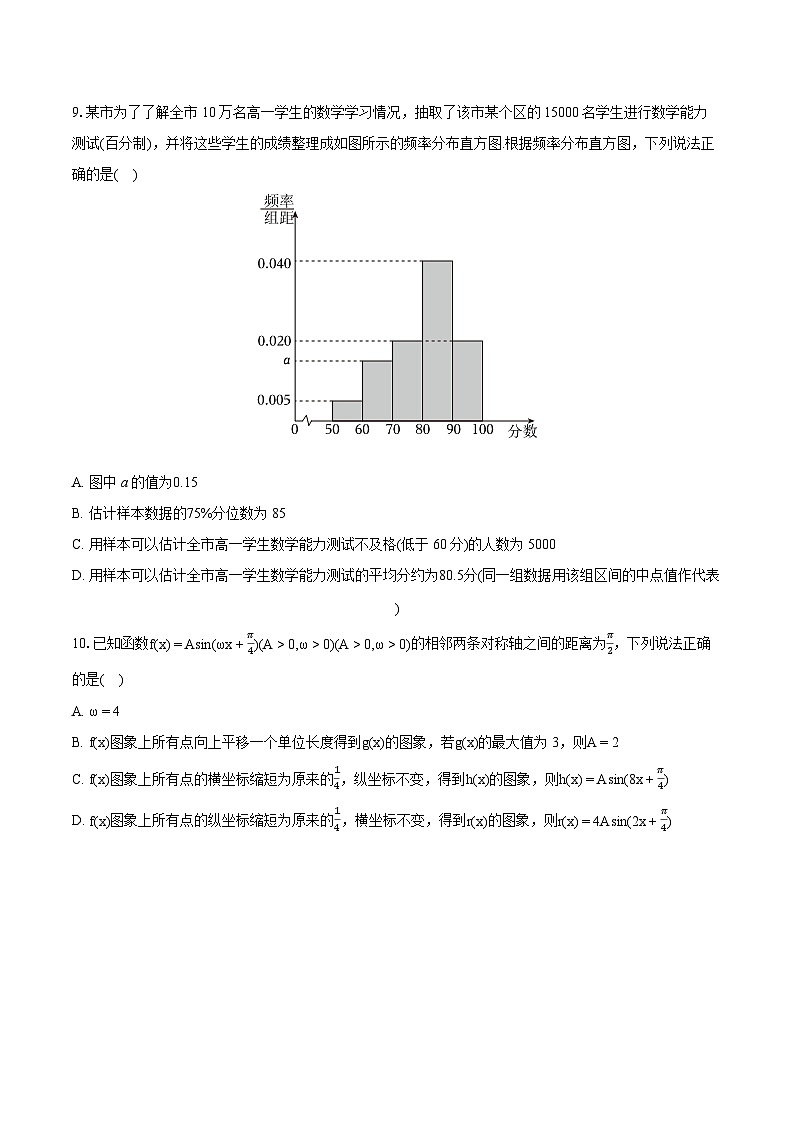
9.某市为了了解全市10万名高一学生的数学学习情况，抽取了该市某个区的15000名学生进行数学能力测试(百分制)，并将这些学生的成绩整理成如图所示的频率分布直方图.根据频率分布直方图，下列说法正确的是( )
A. 图中a的值为0.15
B. 估计样本数据的75%分位数为85
C. 用样本可以估计全市高一学生数学能力测试不及格(低于60分)的人数为5000
D. 用样本可以估计全市高一学生数学能力测试的平均分约为80.5分(同一组数据用该组区间的中点值作代表)
10.已知函数f(x)=Asin(ωx+π4)(A>0,ω>0)(A>0,ω>0)的相邻两条对称轴之间的距离为π2，下列说法正确的是( )
A. ω=4
B. f(x)图象上所有点向上平移一个单位长度得到g(x)的图象，若g(x)的最大值为3，则A=2
C. f(x)图象上所有点的横坐标缩短为原来的14，纵坐标不变，得到h(x)的图象，则h(x)=Asin(8x+π4)
D. f(x)图象上所有点的纵坐标缩短为原来的14，横坐标不变，得到r(x)的图象，则r(x)=4Asin(2x+π4)
11.如图，在边长为1的正方形ABCD中，E，F分别为CD，BC的中点，以A为圆心，AB为半径作圆，得到重叠部分为扇形DAB.连接AF，AE，分别交弧BD于P，H.下列说法正确的是( )
A. AE|AE|=AH
B. cs∠HAP=45
C. {HP,DB}可作为一个基底
D. AC= 53AH+ 53AP
12.如图，已知长方体ABCD−A1B1C1D1的三条棱长分别为AB=a，BC=b，BB1=c，a，b，c为常数，且满足b≤a，c=2a.点M为A1D1上的动点(不与A1，D1重合)，过点C作截面α，使α⊥BM，α，α分别交BB1，AB于点E，F.下列说法正确的是( )
A. 截面α是三角形
B. 截面α的周长为定值
C. 存在点M，使CF⊥CE
D. CF2+6CE2−2EF2为定值
三、填空题：本题共4小题，每小题5分，共20分。
13.已知锐角三角形ABC中，内角A，B，C所对的边分别为a，b，c，△ABC的面积为14ab，则C=______.
14.已知e1，e2为不共线的单位向量，所成角为60∘，若向量a=e1+2e2，b=e1−e2，则a⋅b的值为______.
15.某银行发行了甲，乙两款理财产品，一名投资者有意向去投资这两款理财产品.已知这名投资者选择投资甲，乙两款理财产品相互独立，且投资甲产品的概率为15，投资乙产品的概率为14，则该投资者两种产品都不投资的概率为______.
16.如图，在直角梯形ABCD中，AB//CD，AB⊥AD，AD=3，若以A为圆心，AD为半径的圆与BC相切，切点为Q，则AQ⋅AC的值为______.
四、解答题：本题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题10分)
设复数z=1+bi，b∈R，若z1+2i∈R.
(1)求|z|；
(2)z−记为z的共轭复数，计算(z+z−)2+(z−z−)2的值.
18.(本小题12分)
山东淄博有着丰富的烧烤文化，淄博烧烤以其独特的口味和制作方法，吸引了大量的食客，今年的“五一”假期更是游客“进淄赶烧”的高峰期.某商家为了提高自己的竞争力，举行了消费抽奖活动，活动规则如下：每消费满100元，会获得一次抽奖机会，奖项为“5元烧烤优惠券”“10元烧烤优惠券”以及“谢谢惠顾”.已知抽中“5元烧烤优惠券”的概率为12，抽中“10元烧烤优惠券”的概率为13，并且每次抽奖互不影响.
(1)求抽到“谢谢惠顾”的概率；
(2)某位客人消费了200元，求这位客人能抽到总计10元烧烤优惠券的概率.
19.(本小题12分)
如图，已知正方形ABCD所在平面与等腰直角三角形EAB所在平面相互垂直.以AE为直径，在平面EAB内作半圆(半圆位于EA的左侧)，点F为弧AE上的一点.
(1)证明：EF⊥平面ADF；
(2)若点F为弧AE的中点，求二面角F−BD−A的正切值.
20.(本小题12分)
为调查某校高一学生的数学学习情况以及男女生学习水平的差异，采用分层随机抽样的方式从高一年级抽取n人参加数学知识竞赛.已知该校高一男女生的人数比为1：2，抽取了20名男生参加数学知识竞赛，他们的成绩记为⋯，20)，其中xi分别为：8，3，2，4，8，5，5，7，7，6，8，5，5，6，4，9，6，8，6，8.
(参考数据：i=120xi=120，i=120xi2=788)
(1)求样本总人数n；
(2)求男生数学知识竞赛成绩的第60百分位数以及方差；
(3)若女生数学知识竞赛成绩的平均数为3，方差为10.3，求样本总方差.
21.(本小题12分)
如图所示，在一块面积为50003πm2的圆心角为π3的扇形POQ空地中(如图1：扇形POQ，∠QOP=π3)，要建设一座长方体的高楼(如图2：长方体ABCD−A1B1C1D1).由于建设需求，点C需在弧PQ上(如图3).为了消防安全，楼层建设不能太高，OC1与地面OPQ所成的角最大为π4.
(1)求楼高CC1的最大值；
(2)求这座高楼体积的最大值.
22.(本小题12分)
在△ABC中，设内角A，B，C所对的边分别为a，b，c.若AB⋅AC+2BA⋅BC=3CA⋅CB.
(1)证明：a2+2b2=3c2；
(2)若sin(B−A)+sinC=7sinA，求csA的值.
答案和解析
1.【答案】C
【解析】解：由题意得，f(x)=sinxcsx=12×2sinxcsx=12sin2x，
所以函数的最小正周期为2π2=π，
故选：C.
根据二倍角的正弦公式化简函数解析式，再由周期公式求出函数的周期即可．
本题考查二倍角的正弦公式，以及三角函数的周期公式应用，熟练掌握公式是解题的关键．
2.【答案】A
【解析】解：△ABC中，由正弦定理可得asinA=bsinB，即 2sinA= 3 32，∴sinA= 22，
∴A=π4，或 A=3π4 (舍去，因为A不是最大角)，
故选：A.
△ABC中，由正弦定理可得sinA= 22，由于a0，
∴b=−a，2a>0，
∴a>0，b0.75，
前3个矩形条的面积为：1−10×(0.02+0.04)=0.40，所以g(x)的最大值为A+1，故A+1=3，解得A=2，B正确；
C选项，由图象上所有点的横坐标缩短为原来的14，纵坐标不变，得h(x)=Asin(8x+π4)，C正确；
D选项，图象上所有点的纵坐标缩短为原来的14，横坐标不变，得r(x)=14Asin(2x+π4)，D错误．
故选：BC.
A选项，由题目条件得到f(x)的最小正周期，从而得到ω=2；B选项，得到g(x)=Asin(2x+π4)+1，故根据最大值列出方程，求出A=2；CD选项，根据伸缩变换的性质得到答案．
本题主要考查三角函数的图象和性质，根据条件求出函数的周期和ω的值，利用图象变换进行判断是解决本题的关键，是中档题．
11.【答案】ABD
【解析】解：对于A，AE|AE|表示AE方向上的单位向量，|AH|=1，
且AH与AE方向相同，∴AE|AE|=AH，故A正确；
对于B，|AE|=|AF|= 12+(12)2= 52，
∴cs∠FAB=cs∠EAD=1 52=2 5，
sin∠FAB=sin∠EAD=12 52=1 5，
∴cs∠HAP=cs(π2−2∠FAB)=sin(2∠FAB)
=2sin∠FABcs∠FAB=45，故B正确；
对于C，连接EF，HP，BD，
由于|AH||AE|=|AP||AF|，∴EF//HP，
由于E，F分别是CD，BC的中点，∴EF//BD，
∴HP//BD，故{HP,DB}不能作为一个基底，故C错误；
对于D，|AH||AE|=|AP||AF|=1 52=2 5,|AH|=2 5|AE|,|AP|=2 5|AF|，
53AH+ 53AP= 53×2 5AE+ 53×2 5AF=23AE+23AF
=23(AD+12AB)+23(AB+12AD)
=AB+AD=AC，故D正确．
故选：ABD.
根据单位向量，诱导公式、二倍角公式、基底等知识对选项进行分析，从而确定正确答案．
本题主要考查平面向量的线性运算，考查运算求解能力，属于中档题．
12.【答案】AD
【解析】解：以D为原点，DA，DC，DD1所在直线分别为x，y，z轴建立空间直角坐标系；
则B(b,a,0)，C(0,a,0)，设M(t,0,2a)，0