专题26.3实际问题与反比例函数（限时满分培优训练）-九年级数学下册尖子生培优必刷题人教版

这是一份专题26.3实际问题与反比例函数（限时满分培优训练）-九年级数学下册尖子生培优必刷题人教版，文件包含专题263实际问题与反比例函数限时满分培优训练-九年级数学下册尖子生培优必刷题原卷版人教版docx、专题263实际问题与反比例函数限时满分培优训练-九年级数学下册尖子生培优必刷题解析版人教版docx等2份试卷配套教学资源，其中试卷共34页， 欢迎下载使用。
班级：___________________ 姓名：_________________ 得分：_______________
注意事项：
本试卷满分100分，试题共23题，其中选择10道、填空6道、解答7道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2022秋•阜平县期末）小华以每分钟x个字的速度书写，y分钟写了300个字，则y与x之间的函数关系式为（ ）
A．y=x300B．y=300xC．y＝300﹣xD．y=300−xx
【答案】B
【分析】此题可根据等量关系“300＝速度×时间”，把相关数值代入即可求解．
【解答】解：由题意得：xy＝300，
∴y=300x，
故选：B．
【点评】解决本题的关键是得到书写总量的等量关系，y与x间的函数关系式应用含x的代数式表示出y．
2．（2023•浙江二模）已知京沪线铁路全程为1463km，一列火车从北京开往上海，记火车全程的行驶时间为t（h），火车行驶的平均速度为v（km/h），则t关于v的函数关系图象大致是（ ）
A．B．
C．D．
【答案】C
【分析】由题意，有全程除以平均速度等于全程所用时间．列式求解．
【解答】解：由题意，有全程除以平均速度等于全程所用时间．
即：t=1463v，
故选：C．
【点评】本题考查了路程与平均速度之间的关系式，本题很简单的逻辑关系．
3．（2023•蔚县校级模拟）如图1，某长方体A，B，C三个面的面积之比是2：6：3，当A，B，C三个面分别接触地面时，水平地面所受压强分别为p1，p2，p3．已知p=FS满足的函数图象，如图2所示，其中p是压强，F是压力（物体放在水平地面上，物体对地面的压力等于该物体的重力），S是受力面积，则p1，p2，p3的大小关系为（ ）
A．p1＞p3＞p2B．p2＞p3＞p1C．p2＞p1＞p3D．p1＞p2＞p3
【答案】A
【分析】直接利用反比例函数的性质进而分析得出答案．
【解答】解：∵p=FS，F＞0，
∴当S＞0时，p随S的增大而减小，
∵长方体A，B，C三个面的面积之比是2：6：3，
∴p1＞p3＞p2．
故选：A．
【点评】此题主要考查了反比例函数的性质，正确把握反比例函数的性质是解题关键．
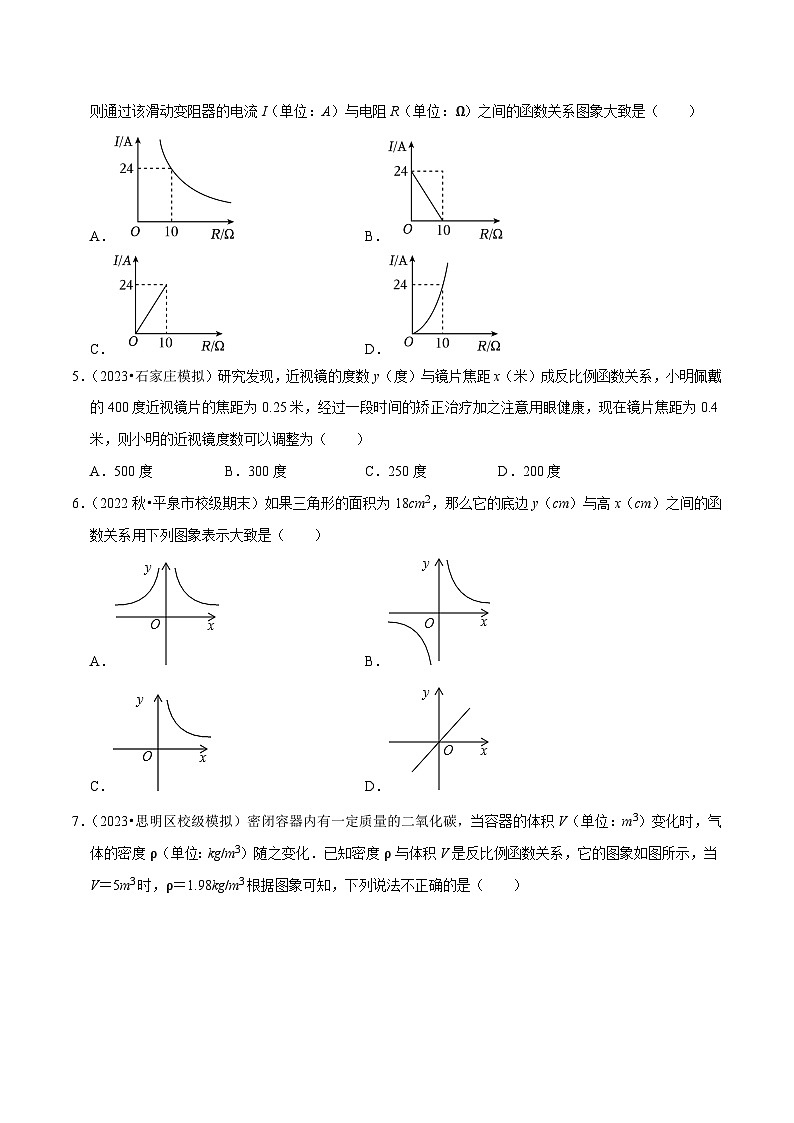
4．（2023•石家庄二模）小明学习了物理中的欧姆定律发现：电阻两端的电压＝电流强度×电流通过的电阻．已知某滑动变阻器两端电压恒定，当变阻器的电阻调节为10Ω时，测得通过该变阻器的电流为24A，则通过该滑动变阻器的电流I（单位：A）与电阻R（单位：Ω）之间的函数关系图象大致是（ ）
A．B．
C．D．
【答案】A
【分析】因为电阻两端的电压＝电流强度×电流通过的电阻，所以I=UR，代入R＝10时，I＝24，求出U，得到I与R的函数关系式，即可得到答案．
【解答】解：∵电阻两端的电压＝电流强度×电流通过的电阻，
∴I=UR，
∵当R＝10Ω时，I＝24A，
∴U10=24，
∴U＝240（V），
∴I=240R，
∴电流I与电阻R成反比例函数关系，
故答案A符合题意，
答案B是一次函数，故不符合题意，
答案C是正比例函数，故不符合题意，
答案D是二次函数，故不符合题意，
故选：A．
【点评】本题考查了反比例函数的实际应用，电学中欧姆定律，求出I与R的函数关系式是解题的关键．
5．（2023•石家庄模拟）研究发现，近视镜的度数y（度）与镜片焦距x（米）成反比例函数关系，小明佩戴的400度近视镜片的焦距为0.25米，经过一段时间的矫正治疗加之注意用眼健康，现在镜片焦距为0.4米，则小明的近视镜度数可以调整为（ ）
A．500度B．300度C．250度D．200度
【答案】C
【分析】设解析式y=kx（k≠0），把x＝0.25，y＝400，代入式中求出k，再求出x＝0.4时，对应y的值即可．
【解答】解：设y=kx（k≠0），
∵x＝0.25时，y＝400，
∴k0.25=400，
∴k＝100，
∴y与x的函数关系式为：y=100x，
当x＝0.4时，y=1000.4=250，
∴小明的近视镜度数可以调整为250度．
故选：C．
【点评】本题考查了反比例函数的实际应用，读懂题意用待定系数法求出函数解析式是解题关键．
6．（2022秋•平泉市校级期末）如果三角形的面积为18cm2，那么它的底边y（cm）与高x（cm）之间的函数关系用下列图象表示大致是（ ）
A．B．
C．D．
【答案】C
【分析】根据题意有：xy＝36；故y与x之间的函数图象为反比例函数，且根据x，y实际意义x，y应大于0，其图象在第一象限；即可得出结果．
【解答】解：∵三角形的面积为18cm2，
∴12xy＝18，
∴xy＝36
∴y=36x（y＞0，x＞0）
故选：C．
【点评】现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用实际意义确定其所在的象限．
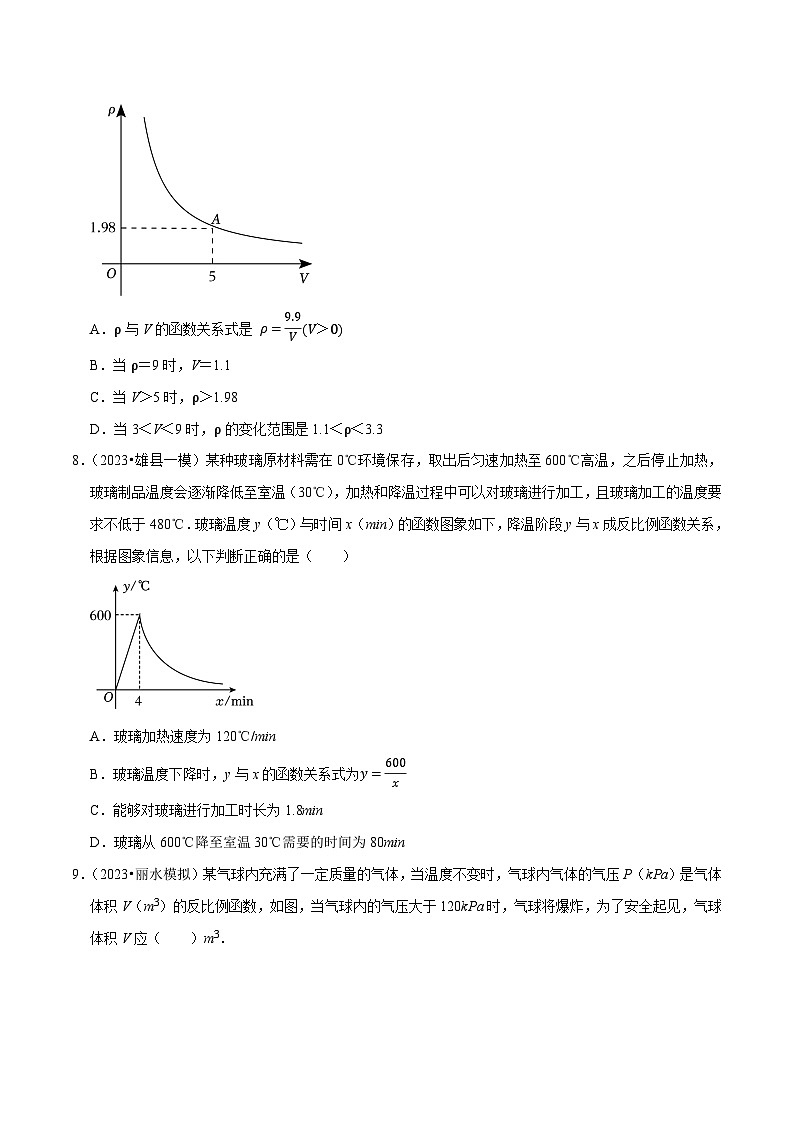
7．（2023•思明区校级模拟）密闭容器内有一定质量的二氧化碳，当容器的体积V（单位：m3）变化时，气体的密度ρ（单位：kg/m3）随之变化．已知密度ρ与体积V是反比例函数关系，它的图象如图所示，当V＝5m3时，ρ＝1.98kg/m3根据图象可知，下列说法不正确的是（ ）
A．ρ与V的函数关系式是 ρ=9.9V(V＞0)
B．当ρ＝9时，V＝1.1
C．当V＞5时，ρ＞1.98
D．当3＜V＜9时，ρ的变化范围是1.1＜ρ＜3.3
【答案】C
【分析】设ρ=kV（k＞0），把（5，1.98）代入求出k，即可判断A；令ρ＝9，求出V，即可判断B；结合图象即可判断C；当V＝3或9时，求出ρ的对应值，即可判断D．
【解答】解：设ρ=kV（k＞0），
把（5，1.98）代入上式得，k5=1.98，
∴k＝9.9，
∴ρ=9.9V，
故选项A正确，不符合题意，
当ρ＝9时，v＝1.1，
故选项B正确，不符合题意，
由图象可得，当V＞5时，0＜ρ＜1.98，
故选项C不正确，符合题意，
当V＝3时，ρ＝3.3，V＝9时，ρ＝1.1，
∴3＜V＜9时，1.1＜ρ＜3.3，
故选项D正确，不符合题意，
故选：C．
【点评】本题考查了反比例函数的应用，数形结合，求出函数解析式是解题的关键．
8．（2023•雄县一模）某种玻璃原材料需在0℃环境保存，取出后匀速加热至600℃高温，之后停止加热，玻璃制品温度会逐渐降低至室温（30℃），加热和降温过程中可以对玻璃进行加工，且玻璃加工的温度要求不低于480℃．玻璃温度y（℃）与时间x（min）的函数图象如下，降温阶段y与x成反比例函数关系，根据图象信息，以下判断正确的是（ ）
A．玻璃加热速度为120℃/min
B．玻璃温度下降时，y与x的函数关系式为y=600x
C．能够对玻璃进行加工时长为1.8min
D．玻璃从600℃降至室温30℃需要的时间为80min
【答案】C
【分析】根据图象中的数据逐项分析求解即可．
【解答】解：∵600÷4＝150，
∴玻璃加热速度为150，
故A选项不合题意；
由题可得，（4，600）在反比例函数图象上，
设反比例函数解析式为y=kx，
代入点（4，600）可得，k＝2400，
∴玻璃温度下降时，y与x的函数关系式是y=2400x，
故B选项不合题意；
∴设玻璃温度上升时的函数表达式为y＝k1x，
由题可得，（4，600）在正比例函数图象上，
代入点（4，600）可得，k＝150，
∴玻璃温度上升时，y与x的函数关系式是y＝150x，
∴将y＝480代入y＝150x，得x＝3.2，
∴将y＝480代入y=2400x，得x＝5，
∴5﹣3.2＝1.8（min），
∴能够对玻璃进行加工时长为1.8min，
故C选项符合题意；
将y＝30代入y=2400x得，x＝80，
∴80﹣4＝76（min），
∴玻璃从600降至室温30需要的时间为76min，
故D选项不符合题意．
故选：C．
【点评】本题考查了反比例函数和一次函数的应用，读懂函数图象，获取信息是解决本题的关键．
9．（2023•丽水模拟）某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（kPa）是气体体积V（m3）的反比例函数，如图，当气球内的气压大于120kPa时，气球将爆炸，为了安全起见，气球体积V应（ ）m3．
A．V≥45B．V＜54C．V＜45D．V≥54
【答案】A
【分析】由题意得P与V成反比例，设气球内气体的气压P和气体的体积V之间的函数关系式为P=kV（k＞0），代入（1.6，），求出解析式，由P≤120，求出V的范围即可．
【解答】解：设气球内气体的气压P和气体的体积V之间的函数关系式为P=kV（k＞0），
∵图象过（1.6，60），
∴60=k1.6，
解得，k＝96，
∴P=96V，
∵在第一象限内P随V的增大而减小，
∴当P≤120时，V≥45，
故选：A．
【点评】本题考查了反比例函数的应用，解题的关键是根据图象上已知点的坐标，利用待定系数法求出函数解析式．
10．（2023春•宝丰县月考）2022年11月，天舟五号货运飞船搭载的燃料电池载荷项目顺利完成在轨实验任务，完成了中国空间燃料电池首次在轨实验，小明通过查阅资料了解到，科技人员通常要检验飞船舱体的气密性．他设计了如图甲所示的检测电路，电源电压保持不变，R0为100Ω的定值电阻，R为压力传感器，其阻值随环境气压的变化规律如图乙所示，将R置于舱体中，舱体置于真空室中，舱体不漏气时，电压表示数为200V，舱体内气压为1.0×105Pa．（电流，电压和电阻之间的关系：I=UR）则下列说法错误的是（ ）
A．当压力传感器的阻值逐渐增加时，舱体内气压逐渐减小
B．舱体不漏气时，可测得压力传感器的阻值为10Ω
C．舱体漏气时，电压表的示数小于200V
D．舱体漏气时，电路中的总电阻也在减小
【答案】D
【分析】根据图象即可判断A、B选项；当舱体漏气时，气压减小，压力传感器的阻值R增大，电路总电阻增大，总电流减小，由U0＝IR0即可判断C、D选项．
【解答】解：根据图象可知，当压力传感器的阻值逐渐增加时，舱体内气压逐渐减小，故A选项正确，不符合题意；
∵舱体不漏气时，舱体内气压为1.0×105Pa，
∴由图象可知，此时压力传感器的阻值为10Ω，故B选项正确，不符合题意；
当舱体漏气时，气压减小，压力传感器的阻值R增大，电路总电阻增大，
由I=UR可知，总电流减小，
由U0＝IR0可知，U0减小，即电压表的示数小于200V，故C选项正确，不符合题意；
由上述分析可知，当舱体漏气时，气压减小，压力传感器的阻值R增大，电路总电阻增大，故D选项错误，符合题意．
故选：D．
【点评】本题主要考查函数与图象，理解题意，能从函数图象中找到正确的信息解决问题是解题关键．
二、填空题（本大题共6小题，每小题3分，共18分）请把答案直接填写在横线上
11．（2023•丹东一模）某气球内充满了一定量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（m3）的反比例函数，其图象如图所示．当气体体积为1m3时，气压是 96 kPa．
【答案】96．
【分析】设出反比例函数解析式，把A坐标代入可得函数解析式，把v＝1代入得到的函数解析式，可得p．
【解答】解：设pkv，
由题意知120=k0.8，
所以k＝96，
故p=96v；
当v＝1m3时，p=961=96（kPa）；
故答案为：96．
【点评】考查反比例函数的应用；应熟练掌握符合反比例函数解析式的数值的意义．
12．（2023•从化区二模）古希腊科学家阿基米德曾说“给我一个支点，我可以撬动地球”．后来人们把阿基米德的发现“若杠杆上的两物体与支点的距离与其质量成反比例则杠杆平衡”归纳为“杠杆原理”．通俗地说，杠杆原理为：阻力×阻力臂＝动力×动力臂．小伟欲用撬棍撬动一块石头，已知阻力和阻力臂分别为1000N和0.5m．则动力F随动力臂L的变化的函数关系式为 F=500L ．
【答案】F=500L．
【分析】根据阻力×阻力臂＝动力×动力臂，即可得出F与L之间的函数关系．
【解答】解：依题意得：1200×0.5＝FL，
∴F=500L．
故答案为：F=500L．
【点评】此题主要考查了反比例函数的应用，解答此题的关键是读懂题目，理解杠杆原理为：阻力×阻力臂＝动力×动力臂．
13．（2023•临县二模）密闭容器内有一定质量的二氧化碳，当容器的体积V（单位：m3）变化时，气体的密度ρ（单位：kg/m）随之变化．已知密度ρ与体积V是反比例函数关系，它的图象如图所示，当V＝5m3时，ρ＝1.98kg/m3．若3≤V≤9，二氧化碳密度ρ的变化范围 1.1≤ρ≤3.3 ．
【答案】1.1≤ρ≤3.3．
【分析】设ρ=kV(V＞0)，由V＝5m3时，ρ＝1.98kg/m3求出k的值，得到解析式，求出V＝3m3和V＝9m3时对应的ρ的值，即可得到结果．
【解答】解：∵密度ρ与体积V是反比例函数关系，
∴设ρ=kV(V＞0)，
∵当V＝5m3时，ρ＝1.98kg/m3，
∴1.98=k5，
∴k＝1.98×5＝9.9，
∴密度ρ关于体积V的函数解析式为：ρ=9.9V(V＞0)，
观察函数图象可知，ρ随V的增大而减小，
当V＝3m3时，ρ=9.93=3.3（kg/m3），
当V＝9m3时，ρ=9.99=1.1（kg/m3），
∴当3≤V≤9时，1.1≤ρ≤3.3（kg/m3），
即二氧化碳密度ρ的变化范围是1.1≤ρ≤3.3（kg/m3），
故答案为：1.1≤ρ≤3.3．
【点评】本题考查反比例函数的实际应用，掌握反比例函数图象的性质是解题的关键．
14．（2023•龙湾区开学）验光师通过检测发现近视眼镜的度数y（度）与镜片焦距x（米）成反比例，y关于x的函数图象如图所示．经过一段时间的矫正治疗后，小雪的镜片焦距由0.25米调整到0.5米，则近视眼镜的度数减少了 200 度．
【答案】200．
【分析】由已知设y=kx，则有图象知点（0.2，500）满足解析式，代入求k＝100，则解析式为：y=100x，令x＝0.25，x＝0.5时，分别求y的值后作差即可．
【解答】解：设y=kx（k≠0），
∵（0.2，500）在图象上，
∴k＝500×0.2＝100，
∴函数解析式为：y=100x，
当x＝0.25时，y=1000.25=400，
当x＝0.5时，y=1000.5=200，
∴度数减少了400﹣200＝200（度），
故答案为：200．
【点评】本题考查待定系数法求反比例函数解析式，以及反比例函数的实际应用，读懂题意，掌握课本知识是解决问题的关键．
15．（2023春•巴东县期中）一个用电器的电阻是可调节的，其范围为110∽220Ω．已知电压为220V，这个用电器的电路图如图所示，则这个用电器功率的范围是 220w～440w ．
【答案】220w～440w．
【分析】根据功率公式W=U2R，求得W的范围即可求解．
【解答】解：∵W=U2R，电阻的范围为110～220Ω，电压为220V，
当R＝110Ω时，W=2202110=440，
当R＝220时，W=2202220=220，
∴这个用电器功率的范围是220w～440w
故答案为：220w～440w．
【点评】本题考查了反比例函数的应用，熟练掌握反比例函数的性质是解题的关键．
16．（2022秋•信都区校级期末）某品牌热水器中，原有水的温度为20℃，开机通电，热水器启动开始加热（加热过程中水温y℃与开机时间x分钟满足一次函数关系），当加热到80℃时自动停止加热，随后水温开始下降（水温下降过程中水温y℃与开机时间x分钟成反比例函数关系）．当水温降至30℃时，热水器又自动以相同的功率加热至80℃……重复上述过程，如图，根据图象提供的信息，则：
（1）当0≤x≤15时，水温y℃与开机时间x分钟的函数表达式 y＝4x+20 ；
（2）当水温为30℃时，t＝ 40 ；
（3）通电60分钟时，热水器中水的温度y约为 1603℃ ．
【答案】（1）y＝4x+20；
（2）40；
（3）1603℃．
【分析】（1）设直线解析式为y＝kx+b，结合图象点（0，20），（15，80）代入即可得到答案；
（2）设反比例函数解析式为y=kx，结合图象点（15，80）代入求出k，将y＝30代入即可得到答案；
（3）判断出一个循环所用的时间，再判断60分钟是的函数是哪一个函数，代入数据即可计算．
【解答】解：（1）设直线解析式为y＝kx+b，将点（0，20），（15，80）代入可得，b=2015k+b=80，
解得k=4b=20，
故答案为：y＝4x+20；
（2）当水温下降时，设反比例函数解析式为y=kx，将点（15，80）代入可得，k＝15×80＝1200，
∴y=1200x，
当y＝30时，30=1200x，
解得x＝40，
故答案为：40；
（3）当y＝30时，30＝4x+20，解得x＝2.5，
∴从30℃加热到80℃所需要的时间为15﹣2.5＝12.5（分钟）；从80℃降温到30℃所需要的时间为40﹣15＝25（分钟），
∴40+12.5＝52.5（分钟），60﹣52.5＝7.5（分钟）＜25（分钟），
∴当通电60分钟时，处于降温过程，即处于函数y=1200x上，
将x＝15+7.5＝22.5代入y=1200x，
可得y=120022.5=1603℃．
故答案为：1603℃．
【点评】本题考查反比例函数图象与一次函数图象共存问题，解题的关键是求出两个解析式及周期对应的时间．
三、解答题（本大题共7小题，共52分．解答时应写出文字说明、证明过程或演算步骤）
17．（2023秋•株洲期中）如图，小明想要用撬棍撬动一块大石头，已知阻力为1200N，阻力臂长为0.5m．设动力为y（N），动力臂长为x（m）．（杠杆平衡时，动力×动力臂＝阻力×阻力臂，图中撬棍本身所受的重力忽略不计）
（1）求y关于x的函数解析式．
（2）当动力臂长为1.5m时，撬动石头至少需要多大的力？
【答案】（1）y=600x；
（2）当动力臂长为1.5m时，撬动石头至少需要400N的力．
【分析】（1）根据动力×动力臂＝阻力×阻力臂，即可得出y关于x的函数表达式；
（2）将x＝1.5代入（1）中所求解析式，即可得出y的值．
【解答】解：（1）由题意可得：xy＝1200×0.5，
则y=600x，
即y关于x的函数表达式为y=600x；
（2）∵y=600x，
∴当x＝1.5时，y=6001.5=400，
故当动力臂长为1.5m时，撬动石头至少需要400N的力．
【点评】此题主要考查了反比例函数的应用，正确得出y与x之间的关系是解题关键．
18．（2023•船营区一模）已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示：
（1）求电流I关于电阻R的函数解析式；
（2）如果以此蓄电池为电源的用电器的限制电流I不能超过10A，请直接写出该用电器可变电阻R应控制在什么范围？
【答案】（1）电流I与电阻R之间的函数表达式为I=36R．
（2）用电器的可变电阻应大于或等于3.6Ω．
【分析】（1）先由电流I是电阻R的反比例函数，可设I=kR，将点（20，1.8）代入函数解析式，利用待定系数法即可求出这个反比例函数的解析式；
（2）将I≤10代入（1）中所求的函数解析式即可确定电阻的取值范围．
【解答】解：（1）设电流I与电阻R之间的函数表达式为I=kR．
∵函数图象过点（9，4），
∴4=k9，
解得k＝36．
∴电流I与电阻R之间的函数表达式为I=36R．
（2）∵限制电流不能超过10A，
∴36R≤10，
解得R≥3.6，
∴用电器的可变电阻应大于或等于3.6Ω．
【点评】本题考查了反比例函数的应用，解题的关键是正确地从题干中整理出函数模型，并利用函数的知识解决实际问题．
19．（2022秋•代县期末）山西地处黄河中游，是世界上最早最大的农业起源中心之一，是中国面食文化的发祥地，其中的面条文化至今已有两千多年的历史（面条在东汉称之为“煮饼”）．厨师将一定质量的面团做成拉面时，面条的总长度y（m）是面条横截面面积S（mm2）的反比例函数，其图象经过A（4，32），B（a，80）两点（如图）．
（1）求y与S之间的函数关系式；
（2）求a的值，并解释它的实际意义；
（3）某厨师拉出的面条最细时的横截面面积不超过0.8mm2，求这根面条的总长度至少有多长．
【答案】（1）y与x之间的函数表达式为：y=128S（S＞0）；
（2）当面条的横截面积为1.6mm2时，面条长度为80m；
（3）面条的总长度至少为160m．
【分析】（1）直接利用待定系数法得出反比例函数解析式即可；
（2）利用（1）中所求进而得出a的值，得出其实际意义；
（3）利用S＝0.8求出y的值即可得出答案．
【解答】解：（1）设y与x之间的函数表达式为：y=kS（S＞0），
将（4，32）代入可得：k＝128，
∴y与S之间的函数表达式为：y=128S（S＞0）；
（2）将（a，80）代入y=128S可得a＝1.6，
实际意义：当面条的横截面积为1.6mm2时，面条长度为80m；
（3）∵厨师做出的面条横截面面积不超过0.8mm2，
∴y≥1280.8=160，
故面条的总长度至少为160m．
【点评】此题主要考查了反比例函数的应用，正确得出理解y与S代表的意义是解题关键．
20．（2023春•涟水县期末）某医药研究所研制了一种新药，在试验药效时发现：成人按规定剂量服用后，检测到从第10分钟起每分钟每毫升血液中含药量增加0.3微克，第100分钟达到最高，接着开始衰退．血液中含药量y（微克）与时间x（分钟）的函数关系如图，并发现衰退时y与x成反比例函数关系．
（1）a＝ 27 ；
（2）分别求出当10≤x≤100和x＞100时，y与x之间的函数关系式；
（3）如果每毫升血液中含药量不低于12微克时是有效的，求一次服药后的有效时间是多少分钟？
【答案】（1）27；
（2）当10≤x≤100时：y＝0.3x﹣3，
当x＞100时，y=2700x；
（3）175分钟．
【分析】（1）从第10分钟起每分钟每毫升血液中含药量增加0.3微克，第100分钟达到最高，根据经历时间可求得a的值；
（2）当10≤x≤100时设y＝kx+b，代入（10，0）和（100，27）即可；当x＞100时，设y=mx，代入（100，27）即可；
（3）分药效上升阶段与衰退阶段达到12微克，根据两个解析式求出对应时间相减即可．
【解答】解：（1）∵从第10分钟起每分钟每毫升血液中含药量增加0.3微克，第100分钟达到最高，
∴a＝（100﹣10）×0.3＝27，
故答案为：27．
（2）当10≤x≤100时设y＝kx+b，代入（10，0）和（100，27）得：
10k+b=0100k+b=27，
解得：k=0.3b=−3，
∴当10≤x≤100时：y＝0.3x﹣3，
当x＞100时，设y=mx，代入（100，27），
∴m＝100×27＝2700，
当x＞100时，y=2700x；
（3）上升阶段药效达到12微克时间，
根据y＝0.3x﹣3，
令y＝12则12＝0.3x﹣3，
解得：x＝50分钟，
衰退阶段药效达到12微克时间，
由y=2700x，
令y＝12，则12=2700x，
解得：x＝225分钟，
∴一次服药后的有效时间是175分钟．
【点评】本题考查了反比例函数与一次函数的综合应用，理解题意，找准数量关系是解题的关键．
21．（2023春•宿迁期末）通过实验研究发现：初中生在数学课上听课注意力指标随上课时间的变化而变化，上课开始时，学生兴趣激增，中间一段时间，学生的兴趣保持平稳状态，随后开始分散，学生注意力指标y随时间x分钟变化的函数图象如图所示，当0≤x＜10和10≤x＜20时，图象是线段：当20≤x≤45时，图象是反比例函数图象的一部分．
（1）求图中点A的坐标；
（2）王老师在一节数学课上讲解一道数学综合题需要16分钟，他能否经过适当的安排，使学生在听这道综合题讲解时，注意力指标都不低于36？请说明理由．
【答案】（1）20；（2）张老师能经过适当的安排，使学生在听这道综合题的讲解时，注意力指标都不低于36．
【分析】（1）设反比例函数的解析式为y=kx，由C（20，45）求出k，可得D坐标，从而求出A的指标值；
（2）求出AB解析式，得到y≥36时，x≥325，由反比例函数y=900x可得y≥36时，x≤25，根据25−325=935＞17，即可得到答案．
【解答】解：（1）设当20≤x≤45时，反比例函数的解析式为y=kx，将C（20，45）代入得：
45=k20，解得k＝900，
∴反比例函数的解析式为y=900x，
当x＝45时，y=90045=20，
∴D（45，20），
∴A（0，20），即A对应的指标值为20；
（2）设当0≤x＜10时，AB的解析式为y＝mx+n，将A（0，20）、B（10，45）代入得：
20=n45=10m+n，解得m=52n=20，
∴AB的解析式为y=52x+20，
当y≥36时，52x+20≥36，解得x≥325，
由（1）得反比例函数的解析式为y=900x，
当y≥36时，900x≥36，解得x≤25，
∴325≤x≤25时，注意力指标都不低于36，
而25−325=935＞17，
∴张老师能经过适当的安排，使学生在听这道综合题的讲解时，注意力指标都不低于36．
【点评】本题考查函数图象的应用，涉及一次函数、反比例函数及不等式等知识，解题的关键是求出0≤x＜10和20≤x≤45时的解析式．
22．（2023春•灵宝市期末）“杆秤”是人类发明的各种衡器中历史最悠久的一种，是利用杠杆原理来称物体重量的简易衡器、由木制的带有秤星的秤杆、秤砣、秤纽、秤盘等组成，人们可以用秤砣到秤纽的水平距离来得出秤盘中物体的重量．
（1）实验探究
如图1，小华仿照古人制作秤的方法制作了一杆简易“秤”．当秤跎移动到秤纽处时，秤盘内不放重物，秤杆左右两边正好平衡．他将重量为y（斤）的物体放在秤盘内，记录下秤杆平衡时秤砣到秤纽的距离x（厘米）．下表中的数据为小华若干次称重时所记录的一些数据．
（2）实践应用
①在图2的坐标系中描出上而表格中各组数值所对应的点；
②根据①中点的分布特点，判断y与x的函数关系，并求出y关于x的函数解析式；
③若小华制作的秤杆的最大长度为60厘米，则秤盘内物体的最大重量为多少斤？
【答案】（1）答案见解答过程；
（2）y=12x；
（3）30斤．
【分析】（1）根据表格中的数值，直角坐标系中描出各点即可；
（2）观察直角坐标系中的各点可得出y是x的正比例函数，然后设正比例函数的解析式为y＝kx，把（1，0.5）代入求出k的值即可（也可以设为一次函数y＝kx+b，然后将（1，0.5），（2，1）代入求出k，b的值即可）；
（3）对于（2）中所求的函数解析式，求出当x＝60时所对应的y的值即可．
【解答】解：（1）描点如下：
（2）y是x的正比例函数．
设正比例函数的解析式为y＝kx，把（1，0.5）代入y＝kx，得：k=12，
∴正比例函数的解析式为y=12x；
（3）对于y=12x，y随x的增大而增大，
∴当x＝60时，y＝30，
∴当秤杆的最大长度为60厘米时，秤盘内物体的最大重量为30斤．
【点评】此题主要考查了正比例函数的实际应用，解答此题的关键是理解题意，熟练掌握待定系数法求正比例函数解析式，以及求函数值的方法．
23．（2023•佛山模拟）一定电压（单位：V）下电流I（A）和电阻R（Ω）之间成反比例关系，小明用一个蓄电池作为电源组装了一个电路如图1所示，通过实验，发现电流I（A）随着电阻R（Ω）值的变化而变化的一组数据如表格所示．
请解答下列问题：
（1）这个蓄电池的电压值是
（2）请在图2的坐标系中，通过描点画出电流I和电阻R之间的关系图象，并直接写出I和R之间的函数关系式；
（3）若该电路的最小电阻值为1.5Ω，请求出该电路能通过的最大电流是多少．
【答案】（1）48．
（2）I=48R．
（3）32A．
【分析】（1）根据电压＝电流×电阻即可求解；
（2）先由电流I是电阻R的反比例函数，可设I=kR，利用待定系数法即可求出这个反比例函数的解析式；
（3）将R＝1.5Ω代入函数关系式后求得电流的值即可．
【解答】解：（1）根据电压＝电流×电阻，
∴蓄电池的电压值是24×2＝48（V）．
（2）设I=kR，
将点（6，8）代入得8=k6，
∴k＝48，
∴I=48R；
（3）当R＝1.5时，I=481.5=32，
电路能通过的最大电流是32A．
【点评】本题考查了反比例函数的应用，从实际问题中整理出反比例函数模型是解决此类问题的关键．
x/厘米
1
2
4
7
11
12
y/5
0.5
1.0
2.0
3.5
5.5
6.0
R（Ω）
…
2
3
4
6
12
…
I（A）
…
24
16
12
8
4
…