专题17 旋转相似模型（教师版）-中考数学几何模型重点突破讲练

这是一份专题17 旋转相似模型（教师版）-中考数学几何模型重点突破讲练，共33页。


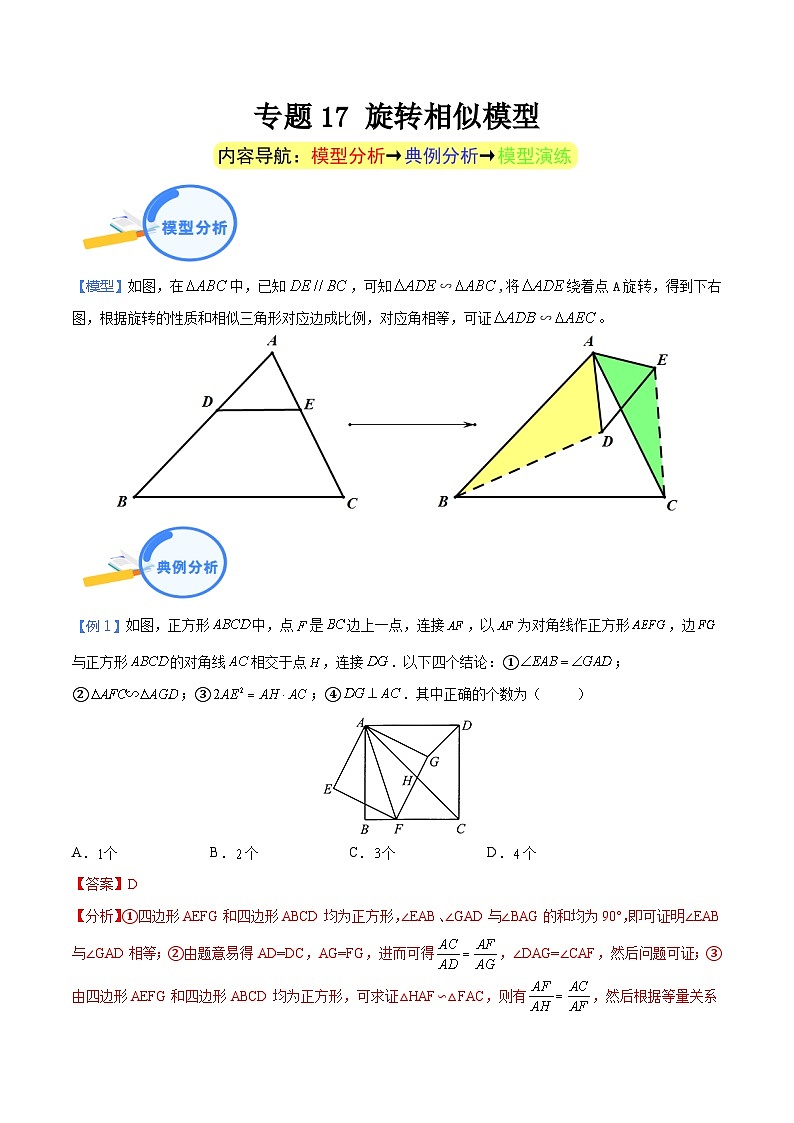
【模型】如图，在中，已知，可知∽,将绕着点A旋转，得到下右图，根据旋转的性质和相似三角形对应边成比例，对应角相等，可证∽。
【例1】如图，正方形中，点是边上一点，连接，以为对角线作正方形，边与正方形的对角线相交于点，连接．以下四个结论：①；②；③；④．其中正确的个数为（ ）
A．个B．个C．个D．个
【答案】D
【分析】①四边形AEFG和四边形ABCD均为正方形，∠EAB、∠GAD与∠BAG的和均为90°，即可证明∠EAB与∠GAD相等；②由题意易得AD=DC，AG=FG，进而可得，∠DAG=∠CAF，然后问题可证；③由四边形AEFG和四边形ABCD均为正方形，可求证△HAF∽△FAC，则有，然后根据等量关系可求解；④由②及题意知∠ADG=∠ACF=45°，则问题可求证．
【解析】解：①∵四边形AEFG和四边形ABCD均为正方形
∴∠EAG=∠BAD=90°
又∵∠EAB=90°-∠BAG，∠GAD=90°-∠BAG
∴∠EAB=∠GAD
∴①正确
②∵四边形AEFG和四边形ABCD均为正方形
∴AD=DC，AG=FG
∴AC=AD，AF=AG
∴，
即
又∵∠DAG+∠GAC=∠FAC+∠GAC
∴∠DAG=∠CAF
∴
∴②正确
③∵四边形AEFG和四边形ABCD均为正方形，AF、AC为对角线
∴∠AFH=∠ACF=45°
又∵∠FAH=∠CAF
∴△HAF∽△FAC
∴
即
又∵AF=AE
∴
∴③正确
④由②知
又∵四边形ABCD为正方形， AC为对角线
∴∠ADG=∠ACF=45°
∴DG在正方形另外一条对角线上
∴DG⊥AC
∴④正确
故选：D．
【例2】如图，正方形的边长为8，线段绕着点逆时针方向旋转，且，连接，以为边作正方形，为边的中点，当线段的长最小时，______．
【答案】
【分析】连接BD，BF，FD，证明△EBC∽△FBD，根据题意，知道M，F，D三点一线时，FM最小，然后过点M作MG⊥BD，垂足为G，根据等腰直角三角形的性质、勾股定理分别求出MG和DG的长，再根据正切的定义计算即可．
【解析】解：连接BD，BF，FD，如图，
∵，
∴，
∵∠FBD+∠DBE=45°，∠EBC+∠DBE=45°，
∴∠FBD=∠EBC，
∴△EBC∽△FBD，
∴∠FDB=∠ECB，，
∴DF=，
由题意知：FM、DF、DM三条线段满足FM+DF≥MD，其中DM、DF的值一定，
∴当M，F，D三点一线时，FM最小，
过点M作MN⊥BD，垂足为G，
∵∠MBN=45°，BM=AB=4，
∴MN=BN=2，
∵MD==4，
∴DG==6，
∴=，
故答案为：．
【例3】【问题发现】如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D为斜边BC上一点（不与点B，C重合），将线段AD绕点A顺时针旋转90°得到AE，连接EC，则线段BD与CE的数量关系是______，位置关系是______；
【探究证明】如图2，在Rt△ABC和Rt△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，将△ADE绕点A旋转，当点C，D，E在同一条直线上时，BD与CE具有怎样的位置关系，说明理由；
【拓展延伸】如图3，在Rt△BCD中，∠BCD＝90°，BC＝2CD＝4，过点C作CA⊥BD于A．将△ACD绕点A顺时针旋转，点C的对应点为点E．设旋转角∠CAE为（0°＜＜360°），当C，D，E在同一条直线上时，画出图形，并求出线段BE的长度．
【答案】BD＝CE，BD⊥CE； BD⊥CE，理由见解析；图见解析，
【分析】（1）证明△BAD≌△CAE，根据全等三角形的性质解答；
（2）连接BD，根据全等三角形的判定和性质以及垂直的定义即可得到结论；
（3）如图3，过A作AF⊥EC，根据相似三角形的判定和性质以及勾股定理即可得到结论．
【解析】解：（1）BD＝CE，BD⊥CE；
（2）BD⊥CE．理由如下：在Rt△ABC和Rt△ADE中，AB＝AC，AD＝AE，∠AEC＝45°，∵∠CAB＝∠DAE＝90°，∴∠BAD＝∠CAE，∴△CEA≌△BDA，
∴∠BDA＝∠AEC＝45°，∴∠BDE＝∠BDA＋∠ADE＝90°，∴BD⊥CE．
（3）如图所示，过点A作AF⊥CE，垂足为点F．
根据题意可知，Rt△ABC∽Rt△AED，∠BAC＝∠EAD，
∴，∴．
∵∠BAC＝∠EAD＝90°，∴∠BAE＝∠CAD，∴△BAE∽△CAD，
∴∠BEA＝∠CDA，∠BEC＋∠DEA＝∠DEA＋90°，
∴∠BEC＝90°，∴BE⊥CE．
在旋转前，在Rt△BCD中，∠BCD＝90°，BC＝2CD＝4，
∴，∵AC⊥BD，
∴，∴．
∴，
在Rt△ACD中，CD边上的高，旋转后，得，
∴．
一、单选题
1．如图，点E是边长为8的正方形ABCD的边CD上一动点，连接AE，将线段AE绕点E逆时针旋转90°到线段EF，连接AF，BF，AF交边BC于点G，连接EG，当AF+BF取最小值时，线段EG的长为（ ）
A．8B．7C．9D．
【答案】D
【分析】过点F作FP⊥CD交DC的延长线于点P，作直线CF，首先证明△PEF≌△DAE，得PF＝DE，PE＝AD，再证明点F在∠BCP的平分线上，作点B关于直线CF的对称点M，连接AM交直线CF于点F，此时，AF＋BF最小，设DE＝x，由图1知，PE＝PC＝DE＝x，则PM＝CM−PC＝8−x，由△MPF∽△MCG，得到对应边成比例即可求出x的值，再利用勾股定理即可解决问题．
【解析】解：如图，过点F作FP⊥CD交DC的延长线于点P，作直线CF，
∵四边形ABCD是正方形，
∴AB＝AD＝BC＝CD＝8，∠D＝∠BCD＝90°，AB∥CD，
∴∠D＝∠EPF＝90°，
∴∠AED＋∠DAE＝90°，
由旋转知，AE＝FE，∠AEF＝90°，
∴∠AED＋∠PEF＝90°，
∴∠PEF＝∠DAE，
在△PEF与△DAE中，
∴△PEF≌△DAE（AAS），
∴PF＝DE，PE＝AD，
∴PE＝CD，
∴PE−CE＝CD−CE，
∴PC＝DE，
∵FP⊥CD，
∴∠PCF＝45°，
∴点F在∠BCP的平分线上，
如图2，作点B关于直线CF的对称点M，连接AC、BM，连接AM交直线CF于点F，此时，AF＋BF最小，
∵点B关于直线CF的对称点M，
∴△BFC≌△MFC（ASA），
∴CM＝BC＝AB＝8，
∵ABCD，
∴四边形ABMC为平行四边形，
∴BG＝CG＝BC＝4，
设DE＝x，由图1知，
PE＝PC＝DE＝x，
∴PM＝CM−PC＝8−x，
∵∠BCM＝∠FPM＝90°，
∴PFBC，
∴△MPF∽△MCG，
∴，
即，
解得：x＝，
∴CE＝CD−DE＝8−，
∴，
故选：D．
2．如图，在矩形ABCD中，DE平分交BC于点E，点F是CD边上一点（不与点D重合）．点P为DE上一动点，，将绕点P逆时针旋转90°后，角的两边交射线DA于H，G两点，有下列结论：①；②；③；④，其中一定正确的是（ ）
A．①②B．②③C．①④D．③④
【答案】D
【分析】根据旋转的性质判断得，可判断③正确，证可判断④正确，从而得出结果.
【解析】解：根据旋转的性质可知，，
∵DE平分，
∴，
∴，
∴PH=PD，
∵
∴
在和中，
∵
∴
∴
∵
∴
∴
故③正确；
∵，
∴
∴
即，
故④正确；
根据已知条件无法证明①DH=DE，②DP=DG.
故选：D．
3．如图，中，，，点是重心，将绕着点按顺时针方向旋转，使点A落在BC延长线上的处，此时点B落在点，点G落在点.联结CG、、、.在旋转过程中，下列说法：①；②与相似；③；④点所经过的路程长是.其中正确的个数是（ ）
A．1B．2C．3D．4
【答案】C
【分析】根据旋转的性质即判断①，由旋转的性质可得，进而可得，，即可判断②，根据相似三角形的性质可以判断③，根据弧长公式计算即可判断④．
【解析】解：，，
是等腰直角三角形，
，
，
由旋转的性质可得，故①正确；
如图，连接，
，，点是重心，
，
，
由旋转的性质可得，
，
，，
与相似；
故②正确；
，
故③正确，
④点所经过的路程长是，故④错误，
故选C．
4．如图，四边形为正方形，将绕点逆时针旋转至，点，，在同一直线上，与交于点，延长与的延长线交于点，，．以下结论：
①；②；③；④．其中正确结论的个数为（ ）
A．1个B．2个C．3个D．4个
【答案】D
【分析】利用旋转的性质，正方形的性质，可判断①正确；利用三角形相似的判定及性质可知②正确；证明，得到，即，利用是等腰直角三角形，求出，再证明即可求出可知③正确；过点E作交FD于点M，求出，再证明，即可知④正确．
【解析】解：∵旋转得到，
∴，
∵为正方形，，，在同一直线上，
∴，
∴，故①正确；
∵旋转得到，
∴，，
∴，
∴，
∵，
∴，
∴，
∴，故②正确；
设正方形边长为a，
∵，，
∴，
∵，
∴，
∴，即，
∵是等腰直角三角形，
∴，
∵，，
∴，
∴，即，解得：，
∵，
∴，故③正确；
过点E作交FD于点M，
∴，
∵，
∴，
∵，
∴，
∵，，
∴，
∴，故④正确
综上所述：正确结论有4个，
故选：D
5．如图，在中，，将以点为中心逆时针旋转得到，点在边上，交于点．下列结论：①；②平分；③，其中所有正确结论的序号是（ ）
A．①②B．②③C．①③D．①②③
【答案】D
【分析】根据旋转的性质可得对应角相等，对应边相等，进而逐项分析判断即可求解．
【解析】解：∵将以点为中心逆时针旋转得到，
∴，
，
，
，故①正确；
，
，
，
，
，
平分，故②正确；
，
，
，
，
，
，
故③正确
故选D
二、填空题
6．如图，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE＝∠ADC，BE＝CE＝2，CD＝5，AD＝kAB（k为常数），则BD的长为____．（用含k的式子表示）
【答案】
【分析】连接AC，将△ABD绕点A逆时针旋转至△ACG，连接DG，根据相似三角形的判定与性质求出DG=kBC，然后根据题意推出∠CDG=90°，即可利用勾股定理求解．
【解析】解：如图，连接AC，
∵AE⊥BC，BE＝CE＝2，
∴BC=4，AE垂直平分BC，AB=AC，
将△ABD绕点A逆时针旋转至△ACG，如图所示，连接DG，
则AD=AG，BD=CG，
由旋转的性质可得：∠BAC=∠DAG，
∵AB=AC，AD=AG，
∴△ABC∽△ADG，
∴，
∵AD＝kAB，
∴DG=kBC=4k，
∵∠BAE+∠ABC=90°，∠BAE=∠ADC，
∴∠ABC+∠ADC=90°，
∵△ABC∽△ADG，
∴∠ABC=∠ADG，
∴∠ADG+∠ADC=90°，
即：∠CDG=90°，
∴，
∴．
7．如图，在△ABC中，AB＝5，D为边AB上－动点，以CD为一边作正方形CDEF，当点D从点B运动到点A时，点E运动的路径长为_________．
【答案】5
【分析】如图，构造等腰Rt△CBG，∠CBG=90°，则由△CGE∽△CBD，得GE=BD，即可求得点E运动的路径长．
【解析】如图：作GB⊥BC于B，取GB=BC，
当点D与点B重合时，则点E与点G重合，
∴∠CBG=90°，
∴CG=BC，∠GCB=45，
∵四边形CDEF是正方形，
∴CE=DC，∠ECD=45，
∴∠BCD+∠DCG =∠GCE+∠DCG =45，
∴∠BCD =∠GCE，且，
∴△CGE∽△CBD，
∴，即GE=BD，
∵BD=5，
∴点E运动的路径长为GE=BD=5．
8．已知正方形DEFG的顶点F在正方形ABCD的一边AD的延长线上，连结AG，CE交于点H，若，，则CH的长为________.
【答案】
【分析】连接EG，与DF交于N，设CD和AH交于M，证明△ANG∽ADM，得到，从而求出DM的长，再通过勾股定理算出AM的长，通过证明△ADG≌△CDE得到∠DAG=∠DCE，从而说明△ADM∽△CHM，得到，最后算出CH的长.
【解析】解：连接EG，与DF交于N，设CD和AH交于M，
∴∠GNA=90°，DN=FN=EN=GN，
∵∠MAD=∠GAN，∠MDA=∠GNA=90°，
∴△ANG∽ADM，
∴，
∵，
∴DF=EG=2,
∴DN=NG=1，
∵AD=AB=3，
∴，
解得：DM=，
∴MC=，AM=，
∵∠ADM+∠MDG=∠EDG+∠CDG，
∴∠ADG=∠EDC，
在△ADG和△CDE中，
，
∴△ADG≌△CDE（SAS），
∴∠DAG=∠DCE，
∵∠AMD=∠CMH，
∴∠ADM=∠CHM=90°，
∴△ADM∽△CHM，
∴，
即，
解得：CH=.
9．将一副三角尺（在Rt△ABC中，∠ACB＝90°，∠B＝60°；在Rt△DEF中，∠EDF＝90°，∠E＝45°）如图①摆放，点D为AB的中点，DE交AC于点P，DF经过点C．将△DEF绕点D顺时针方向旋转角α（0°＜α＜60°），DE′交AC于点M，DF′交BC于点N，则＝________．
【答案】
【分析】根据直角三角形斜边上的中线等于斜边的一半可得CD＝AD＝BD＝AB，根据等边对等角求出∠ACD＝∠A，再求出∠ADC＝120°，再根据∠ADE＝∠ADC﹣∠EDF计算得30°，根据同角的余角相等求出∠PDM＝∠CDN，再根据然后求出△BCD是等边三角形，根据等边三角形的性质求出∠BCD＝60°，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CPD＝60°，从而得到∠CPD＝∠BCD，再根据两组角对应相等，两三角形相似判断出△DPM和△DCN相似，再根据相似三角形对应边成比例可得结论．
【解析】解：∵∠ACB＝90°，点D为AB的中点，
∴CD＝AD＝BD＝AB，
∴∠ACD＝∠A＝30°，
∴∠ADC＝180°﹣30°×2＝120°，
∴∠ADE＝∠ADC﹣∠EDF＝120°﹣90°＝30°；
∵∠EDF＝90°，
∴∠PDM+∠E′DF＝∠CDN+∠E′DF＝90°，
∴∠PDM＝∠CDN，
∵∠B＝60°，BD＝CD，
∴△BCD是等边三角形，
∴∠BCD＝60°，
∵∠CPD＝∠A+∠ADE＝30°+30°＝60°，
∴∠CPD＝∠BCD，
∴△DPM∽△DCN，
∴＝，
∵∠ACD＝30°，∠CDP＝90°，
∴＝tan∠ACD＝tan30°＝，
∴＝．
故答案为：．
10．如图，在中，，，，将绕点按逆时针方向旋转得到．连接、，直线、交于点，连接．
（1）与的等量关系是：___；
（2）在旋转过程中，线段的最大值是___．
【答案】
【分析】（1）由旋转可知：，可证，即得，；
（2）取的中点，连接，，设，交于点，由（1）知，得，可得，由是的中点，有，故当，，共线时，最大为．
【解析】解：（1），理由如下：
由旋转可知：，
，，，
，，
，
，
；
故答案为：；
（2）取的中点，连接，，设，交于点，如图：
由（1）知，
，
，
，
是的中点，
，
，
当，，共线时，最大为，
故答案为：．
三、解答题
11．在和中，，，与在同一条直线上，点与点重合，，如图为将绕点顺时针旋转后的图形，连接，，若，求和的面积．
【答案】和的面积分别为2和．
【分析】过点D作DMBC于点M，根据30°所对直角边为斜边一半，分别求出BC、DC的长度，且证BDC∽AEC，在DMC中，可得DM=1，即BDC的面积可求，且，即AEC的面积可求．
【解析】解：如图所示，过点D作DMBC于点M，
∵AC=2，，
∴，
又∵，，
∴在BAC和DEC中，，，由旋转性质知，，，
∴BDC∽AEC，故，
在DMC中，，，
∴，
∴，
∵BDC∽AEC，
∴，∴，
∴BDC和AEC的面积分别为2和．
12．在同一平面内，如图①，将两个全等的等腰直角三角形摆放在一起，点A为公共顶点，．如图②，若△ABC固定不动，把△ADE绕点A逆时针旋转，使AD、AE与边BC的交点分别为M、N点M不与点B重合，点N不与点C重合．
【探究】求证：．
【应用】已知等腰直角三角形的斜边长为4．
(1)的值为______．
(2)若，则MN的长为______．
【答案】(1)8；(2)
【探究】利用三角形外角的性质可证，又由，可证明结论；
【应用】（1）首先求出等腰直角三角形的直角边长，再由，得，则；
（2）由，得，由（1）知，得，从而得出答案．
【解析】
【探究】∵△ABC为等腰直角三角形，，
∴，同理，，
∵，
，
∴，∴；
【应用】（1）∵等腰直角三角形的斜边长为4，
∴，∵，
∴，∴，∴，
故答案为：8；
（2）∵，∴，∵，
∴，∴，
故答案为：．
13．如图1，中，，，点、、分别在三条边上，，．
（1）如图2，将绕点逆时针旋转，点、分别为、的中点，若，求 的长；
（2）如图3，将绕点顺时针旋转，点、为、的中点，直接写出的值．
【答案】（1）7.5；（2）.
【分析】（1）连结，，易得，得到比例线段计算即可
（2）运用三角形相似得到比例线段，计算即可
【解析】（1）连结，，可证，，
（2）
14．如图，在中，．动点P从点A出发，以每秒3个单位长度的速度沿方向绕行一周，动直线从开始，以每秒1个单位长度的速度向右平移，分别交于两点．当点P运动到点A时，直线也停止运动．
（1）求点P到的最大距离；
（2）当点P在上运动时，
①求的值；
②把绕点E顺时针方向旋转，当点P的对应点落在上时，的对应线段恰好与垂直，求此时t的值．
（3）当点P关于直线的对称点为F时，四边形能否成为菱形？若能，直接写出t的值；若不能，请说明理由．
【答案】（1）；（2）①；②；（3）能，
【分析】（1）当点P与点C重合时，点P到AB的距离最大，过点C作CF⊥AB于F，根据面积法求解即可；
（2）①分别求出DG和PG的长，求出，即可得；②证明得即，解方程求解即可；
（3）分当点P在上、当点P在上和当点P在上三种情况列式求解即可．
【解析】解：（1）当点P与点C重合时，点P到的距离最大，
过点C作CF⊥AB于F
∴根据勾股定理，得
∵
∴．
∴当点P与点C重合时，点P到AB的距离最大，最大值为Rt△ABC斜边AB上的高CF，
即点P到的最大距离是．
（2）①当点P在上运动时，设运动时间为，则有，
直线
，
如图，过点D作于点G，则四边形是矩形，
，
，即
，
，即．
②
，
．
∵直线
直线，
，
由旋转的性质，得
，
，
，
即，
．
（3）因为点F是点P关于直线的对称点，即垂直平分，
所以，当也垂直平分时，四边形为菱形．
∵直线
，即
，
①当点P在上时，若垂直平分，则有
，
解得；
②当点P在上时，三点都在x轴上，构不成四边形；
③当点P在上时，若点P在直线的右侧，类比①可得：
，
解得；
若点P在直线的左侧，四点构不成凸四边形．
综上，当时，四边形为菱形．
15．发现规律
（1）如图①，△ABC与△ADE都是等边三角形，直线BD，CE交于点F．直线BD，AC交于点H．求∠BFC的度数．
（2）已知：△ABC与△ADE的位置如图②所示，直线BD，CE交于点F．直线BD，AC交于点H．若∠ABC＝∠ADE＝α，∠ACB＝∠AED＝β，求∠BFC的度数．
应用结论
（3）如图③，在平面直角坐标系中，点O的坐标为（0，0），点M的坐标为（3，0），N为y轴上一动点，连接MN．将线段MN绕点M逆时针旋转60°得到线段MK，连接NK，OK．求线段OK长度的最小值．
【答案】（1）60°；（2）∠BFC＝180°﹣α﹣β；（3）
【分析】（1）由“SAS”可证△BAD≌△CAE，可得∠ABD＝∠ACE，由三角形内角和定理可求解；
（2）通过证明△ABC∽△ADE，可得∠BAC＝∠DAE，，可证△ABD∽△ACE，可得∠ABD＝∠ACE，由外角性质可得∠BFC＝∠BAC，由三角形内角和定理可求解；
（3）由旋转的性质可得△MNK是等边三角形，可得MK＝MN＝NK，∠NMK＝∠NKM＝∠KNM＝60°，如图③，将△MOK绕点M顺时针旋转60°，得到△MQN，连接OQ，可得∠OMQ＝60°，OK＝NQ，MO＝MQ，则当NQ为最小值时，OK有最小值，由垂线段最短可得当QN⊥y轴时，NQ有最小值，由直角三角形的性质可求解．
【解析】解：（1）如图①，
∵△ABC，△ADE是等边三角形，
∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，
∴∠BAD＝∠CAE，
∴△BAD≌△CAE（SAS），
∴∠ABD＝∠ACE，
∵∠ABD+∠FBC＝∠ABC＝60°，
∴∠ACE+∠FBC＝60°，
∴∠BFC＝180°﹣∠FBC﹣∠ACE﹣∠ACB＝60°；
（2）如图②，
∵∠ABC＝∠ADE＝α，∠ACB＝∠AED＝β，
∴△ABC∽△ADE，
∴∠BAC＝∠DAE，，
∴∠BAD＝∠CAE，，
∴△ABD∽△ACE，
∴∠ABD＝∠ACE，
∵∠BHC＝∠ABD+∠BAC＝∠BFC+∠ACE，
∴∠BFC＝∠BAC，
∵∠BAC+∠ABC+∠ACB＝180°，
∴∠BFC+α+β＝180°，
∴∠BFC＝180°﹣α﹣β；
（3）∵将线段MN绕点M逆时针旋转60°得到线段MK，
∴MN＝MK，∠NMK＝60°，
∴△MNK是等边三角形，
∴MK＝MN＝NK，∠NMK＝∠NKM＝∠KNM＝60°，
如图③，将△MOK绕点M顺时针旋转60°，得到△MQN，连接OQ，
∴△MOK≌△MQN，∠OMQ＝60°，
∴OK＝NQ，MO＝MQ，
∴△MOQ是等边三角形，
∴∠QOM＝60°，
∴∠NOQ＝30°，
∵OK＝NQ，
∴当NQ为最小值时，OK有最小值，
由垂线段最短可得：当QN⊥y轴时，NQ有最小值，
此时，QN⊥y轴，∠NOQ＝30°，
∴NQ＝OQ＝，
∴线段OK长度的最小值为
16．将绕点逆时针方向旋转，并使各边长变为原来的倍，得到，我们将这种变换记为．
（1）问题发现
如图①，对作变换得，则______；直线与直线所夹的锐角度数为______．
（2）拓展探究
如图②，中，且，连结，．对作变换得，求的值及直线与直线相交所成的较小角的度数，并就图②的情形说明理由．
（3）问题解决
如图③，中，，，对作变换得，使点、、在同一直线上，且四边形为矩形，请直接写出的值．
【答案】（1），；（2），理由见解析；（3）．
【分析】（1）利用新定义得出的意义，利用旋转的性质得到∽，且相似比为，，进而求出面积比，通过外角的性质得到即可求出直线与直线所夹的锐角度数；
（2）利用新定义得出的意义，得到，，进而可以得到，下证∽，通过题中给的相似比即可求出面积之比，延长交于，通过，，可以证得∽，从而得到的度数，即可得直线与直线相交所成的较小角的度数；
（3）由四边形为矩形，得到，进而求出的度数，利用含角的直角三角形的性质即可得到的值，进而求出的值．
【解析】解：（1）由题意可知：对作变换得，
∽，且相似比为，，
，
，
，，
，
即直线与直线所夹的锐角度数为：．
故答案为：，．
（2）根据题意得：，，
，
，
∽，
相似比，，
，
，
延长交于，如图，
设交于．
，，
∽，
，
，直线与直线相交所成的较小角的度数为．
（3）四边形为矩形，
，
，
，
，
，
在中，，
，
，
即的值为．