高中2.2 基本不等式教学ppt课件

这是一份高中2.2 基本不等式教学ppt课件，共22页。PPT课件主要包含了大胆假设小心求证，基本不等式，新课讲授，几何意义，半弦不大于半径，总结归纳，三当堂训练，四课堂小结等内容，欢迎下载使用。

学习目标1.掌握基本不等式的形式以及推导过程，会用基本不等式解决简单最值问题。2.经历基本不等式的推导与证明过程，提升逻辑推理能力。3.在猜想论证的过程中，体会数学的严谨性。
一、创设情境，几何引入（赵爽弦图）猜想：a,b属于任意实数， 成立，同学们想一想如何证明？
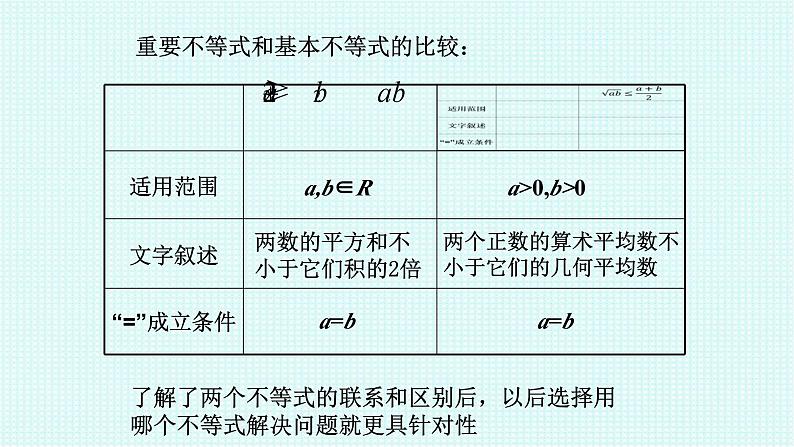
重要不等式： 若a,b∈R，那么a2+b2≥2ab（当且仅当a=b时，取“=”号)
当且仅当a =b时，等号成立.
代数意义：两个正数的算术平均数不小于它们的几何平均数.
两个正数的算术平均数不小于它们的几何平均数
两数的平方和不小于它们积的2倍
重要不等式和基本不等式的比较：
了解了两个不等式的联系和区别后，以后选择用哪个不等式解决问题就更具针对性
基本不等式的证明（方法一）
基本不等式的证明（方法二）
分析法:是要证明结论成立，逐步寻求推证过程中，使每一步成立的充分条件，直到最后，把要证明的结论，归结为判定一个明显成立的条件（已知条件、定理、定义、公理等)为止。所以分析法又叫“逆推证法”，或者“执果索因法”。
1、如图,AB是圆的直径，C是AB上与A、B不重合的一点，AC=a,CB=b,过点C作垂直于AB的弦DE，连AD,BD,则CD=＿＿,半径=＿＿＿＿
２、你能用这个图形得出基本不等式几何解释吗?
两个正数的积为定值时,它们的和有最小值；
两个正数的和为定值时,它们的积有最大值.
思考：求用基本不等式求函数的最值需要满足什么样的条件？
①各项皆为正数；②和或积为定值；③检验等号是否成立
“一正，二定，三相等”
角度一 “不正”问题例 已知x<0,求 的最大值
类型三：间接利用基本不等式
例1 求函数 的最小值.
例2 若 0< x< , 求函数 y=x(1-2x) 的最大值
配凑法：
配凑法:配凑法求解最值，其实质就是先通过代数式变形拼凑出和或积为定值的两项，然后利用基本不等式求解最值，利用基本不等式求解，最注意“一正、二定、三相等”，尤其要注意验证等号成立的条件。
1、下列函数的最小值为2的是
1、重要不等式与基本不等式的内容
2、基本不等式的应用条件
求最值的常用方法(配凑法和常数替换法）