

福建省福州市2023-2024学年高一上学期期末质量检测数学试卷(Word版附答案)
展开2023~2024学年第一学期福州市高一年级期末质量检测
数学试卷
(完卷时间:120分钟;满分:150分)
友情提示:请将所有答案填写到答题卡上!请不要错位、越界答题!
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.
A.B.C.D.
2.命题“,”的否定是
A.,B.,
C.,D.,
3.在下列区间中,方程的实数解所在的区间为
A.B.C.D.
4.已知集合,,则
A.B.C.D.
5.设,则“”是“”的
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
6.已知,,,则
A.B.C.D.
7.已知,则
A.B.C.D.
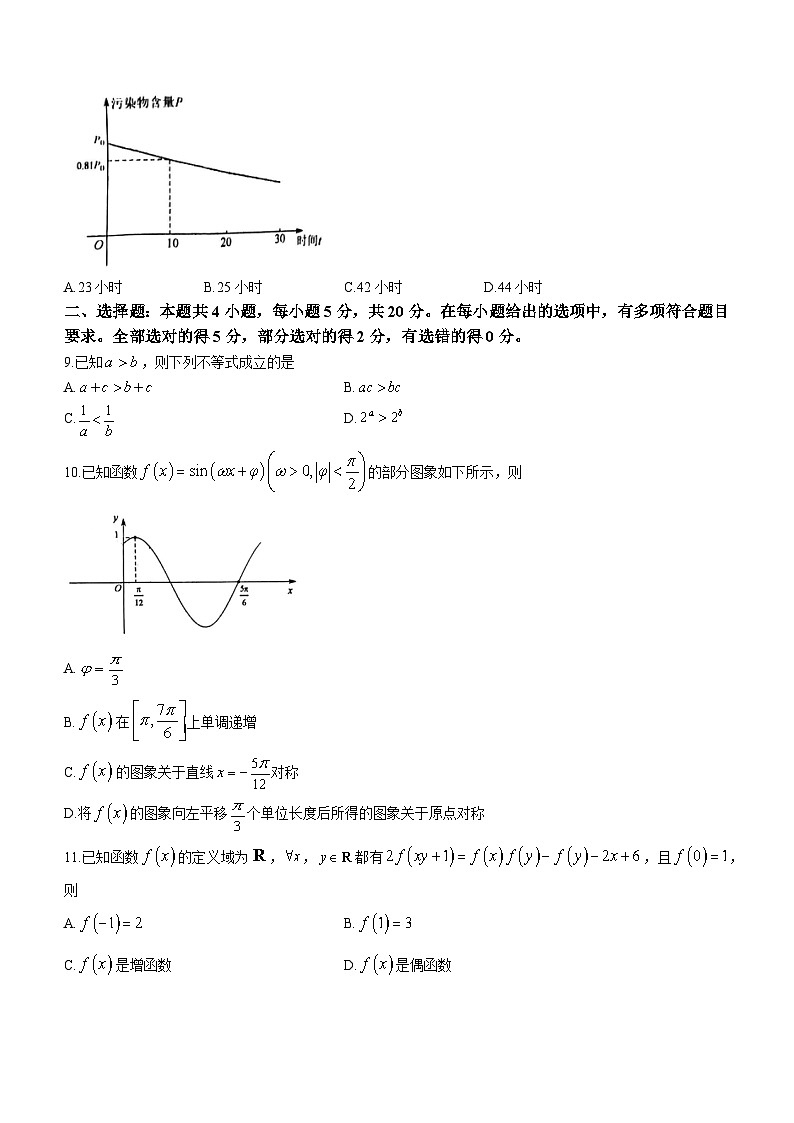
8.某工厂产生的废气经过过滤后排放.已知过滤过程中废气的污染物含量(单位:)与时间(单位:h)的关系为(且,且),其图象如下,则污染物减少至少需要的时间约为
(参考数据:,)
A.23小时B.25小时C.42小时D.44小时
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知,则下列不等式成立的是
A.B.
C.D.
10.已知函数的部分图象如下所示,则
A.
B.在上单调递增
C.的图象关于直线对称
D.将的图象向左平移个单位长度后所得的图象关于原点对称
11.已知函数的定义域为,,都有,且,则
A.B.
C.是增函数D.是偶函数
12.已知函数若关于的方程有3个实数解,,,则
A.
B.
C.
D.关于的方程恰有3个实数解
三、填空题:本题共4小题,每小题5分,共20分。
13.已知函数(且)的图象经过定点,则的坐标是______.
14.已知扇形的弧长是,面积是,则扇形的圆心角(正角)的弧度数为______.
15.已知函数不恒为0,且同时具备下列三个性质:
①;②是偶函数;③,,.
写出一个函数______.
16.用表示函数在闭区间上的最大值,已知.
(1)若,则的取值范围是______.
(2)若,则的取值范围是______.(第一空2分,第二空3分)
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
已知函数.
(1)求的最小值;
(2)若恒成立,求的取值范围.
18.(12分)
已知角的顶点在坐标原点,始边与轴的非负半轴重合,终边经过点.
(1)求,,的值;
(2)将的终边按顺时针方向旋转,此时终边所对应的角为,求的值.
19.(12分)
已知函数,.
(1)求的单调递增区间;
(2)求在区间上的最大值和最小值.
20.(12分)
已知函数.
(1)判断在区间上的单调性,并用定义证明;
(2)解不等式.
21.(12分)
已知函数为奇函数,.
(1)求实数的值;
(2),,使得,求实数的取值范围.
22.(12分)
筒车是我国古代发明的一种水利灌溉工具.如图,假定在水流量稳定的情况下,一个半径为的筒车开启后按逆时针方向做匀速圆周运动,每分钟转1圈、筒车的轴心距离水面的高度为.设筒车上的某个盛水筒到水面的距离为(单位:)(在水面下则为负数).若以盛水筒刚浮出水面时开始计算时间,则与时间(单位:s)之间的关系为.
(1)求,,,的值;
(2)若盛水筒在不同时刻,距离水面的高度相等,求的最小值;
(3)若筒车上均匀分布了12个盛水筒,在筒车运行一周的过程中,求相邻两个盛水筒距离水面的高度差的最大值.
数学参考答案与评分细则
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.D 2.C 3.C 4.B 5.A 6.B 7.B 8.D
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.AD 10.ACD 11.BC 12.ABD
三、填空题:本题共4小题,每小题5分,共20分。
13..14.2.
15..(答案不唯一,如,(且)等均可)
16.(1);(第一空2分) (2).(第二空3分)
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.解:(1).
因为,所以,
所以,
当且仅当,即时,等号成立,
所以的最小值为7.
(2)由(1)知函数的最小值为7,
因为恒成立,所以,
解得,
所以的取值范围是.
18.解法:(1)根据题意可得,,
则,,.
(注:每个三角函数值各2分)
(2)根据题意可得,
所以
解法二:(1)同解法一.
(2)根据题意可得,,
所以,
,
(注:解答过程有体现角与的关系,得1分)
所以.
19.解:(1)根据题意可得,,
即.
因为,所以,
所以,即.
所以
由,得,
所以的单调递增区间为,.
(2)因为,所以,
所以当,即时,;
当,即时,
20.解:(1)函数在区间上单调递增.
(注:结论后置不扣分)
证明:任取,且,则
由,得,
所以,,故,
即,所以,
所以在区间上单调递增.
(2)函数的定义域为,
因为,都有,且,
所以为偶函数.
又由(1)知,在上是单调递增,
所以等价于,
两边平方,得,
解得或,
所以不等式的解集为.
21.解:(1)因为是奇函数,所以,
即,
整理得.
所以.
解得,
当时,,舍去,
当时,函数的定义域为,符合题意.
所以。
(注:定义域没写不扣分,若用特殊值法求出的值,但未检验的扣1分)
(2)设,
根据题意可得,.
由(1)知,
当时,,故.
,
设,函数,.
①当时,,可得,符合题意;
②当时,,图象的对称轴为.
(i)当时,对称轴,
所以在区间上单调递减,故,
由,得,即,
所以;
(ii)当时,
若,即时,,
由,得,
所以;
若,即村,,
由,得,
所以;
综上所述,的取值范围是.
22.解:(1)如图,设筒车与水面的交点为,,连接,
过点作于点,过点分别作于点,于点,
则,
因为筒车转一周需要1分钟,所以,
故.
在中,
,
所以,即.
(2)由(1)知,.
不妨设,由题意得,
故,
所以,或,.
当,时,解得,
故,当且仅当,时,等号成立.
此时的最小值为60;
当,时,解得,
显然当时,取得最小值40.
综上,的最小值为.
(3)设在筒车运行一周的过程中,相邻两个盛水筒距离水面的高度差为
两个相邻的盛水筒的位置分别用和表示,则.
所以
,
当,即,时,
高度差的最大值为
(注:高度差的表达式不唯一)
福建省福州市部分学校教学联盟2023-2024学年高一上学期期末质量检测数学试卷(Word版附解析): 这是一份福建省福州市部分学校教学联盟2023-2024学年高一上学期期末质量检测数学试卷(Word版附解析),共25页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
福建省福州市2023-2024学年高一上学期期末质量检测数学试卷(Word版附解析): 这是一份福建省福州市2023-2024学年高一上学期期末质量检测数学试卷(Word版附解析),共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
福建省三明市2023-2024学年高一上学期期末质量检测数学试题(Word版附答案): 这是一份福建省三明市2023-2024学年高一上学期期末质量检测数学试题(Word版附答案),共13页。试卷主要包含了函数的零点所在的区间为,函数,若,则实数的取值是,函数的部分图象大致是,若,则下列不等式正确的是,下列说法正确的是等内容,欢迎下载使用。












