第10讲 期望方差的实际应用-高二数学同步教学题型讲义（人教A版选择性必修第三册）

这是一份第10讲 期望方差的实际应用-高二数学同步教学题型讲义（人教A版选择性必修第三册），文件包含第10讲期望方差的实际应用原卷版docx、第10讲期望方差的实际应用解析版docx等2份试卷配套教学资源，其中试卷共54页， 欢迎下载使用。

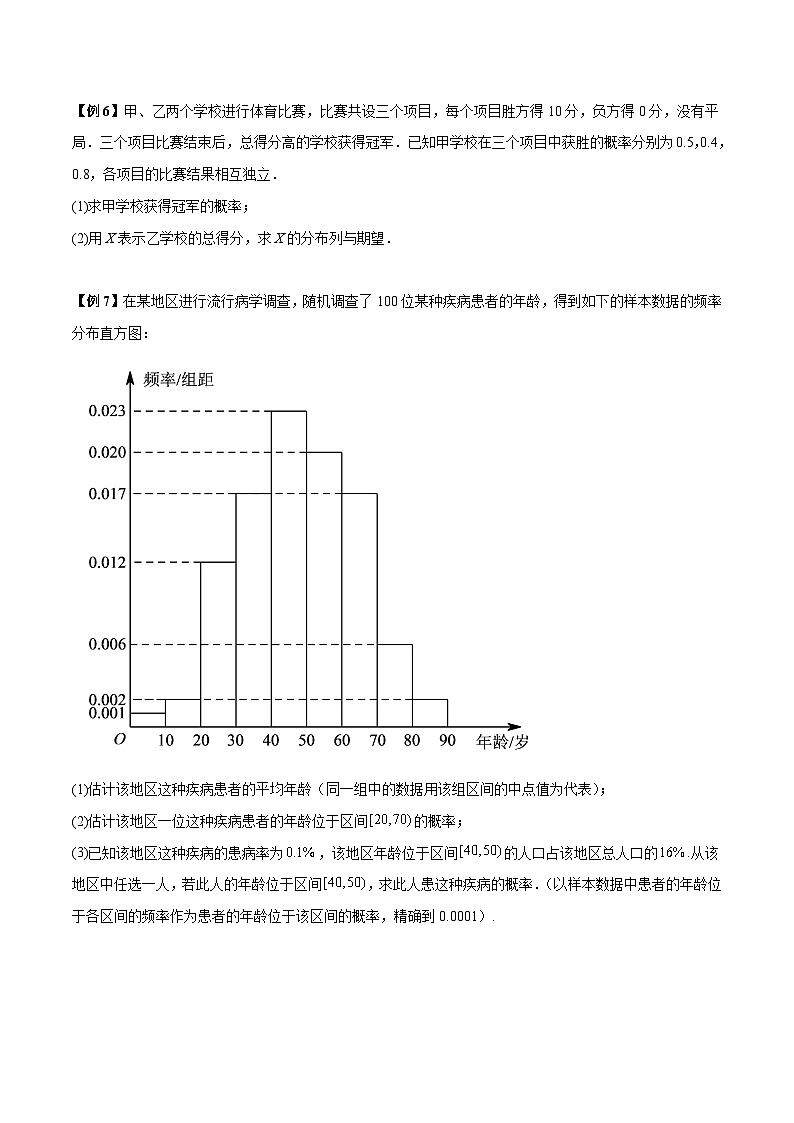
第10讲 期望方差的实际应用【例1】最新研发的某产品每次试验结果为成功或不成功，且每次试验的成功概率为．现对该产品进行独立重复试验，若试验成功，则试验结束；若试验不成功，则继续试验，且最多试验8次．记为试验结束时所进行的试验次数，的数学期望为．(1)证明：；(2)某公司意向投资该产品，若，每次试验的成本为元，若试验成功则获利元，则该公司应如何决策投资？请说明理由．【答案】(1)证明见解析；(2)应该投资，理由见解析【分析】（1）由题意，，，列出分布列，列出，乘公比错位相减法求和，分析可证明；（2）由（1）可得，分析即得解【详解】（1）由题意，故分布列如下：所以的数学期望，记，，作差可得，，则；（2）由（1）可知，则试验成本的期望小于元，试验成功则获利元，且，则该公司应该投资该产品【例2】某市为筛查新冠病毒，需要检验核酸样本是否为阳性，现有且份核酸样本，可采用以下两种检验方式：①逐份检验：对k份样本逐份检验，需要检验k次；②混合检验：将k份样本混合在一起检验，若检验结果为阴性，则k份样本全为阴性，因而这k份样本只需检验1次；若检验结果为阳性，为了确定其中的阳性样本，就需重新采集核酸样本后再对这k份新样本进行逐份检验，此时检验总次数为k+1次.假设在接受检验的核酸样本中，每份样本的检验结果是相互独立的，且每份样本结果为阳性的概率是.(1)若对k份样本采用逐份检验的方式，求恰好经过4次检验就检验出2份阳性的概率（结果用p表示）；(2)若k=20，设采用逐份检验的方式所需的检验次数为X，采用混合检验的方式所需的检验次数为Y，试比较与的大小.【答案】(1)；(2)答案见解析【分析】（1）由独立事件的乘法公式即可求出恰好经过4次检验就检验出2份阳性的概率.（2）由题意知，.Y的可能取值为，求出每个变量对应的概率即可求出，比较与0大小，即可求出答案.(1)记恰好经过4次检验就检验出2份阳性为事件，所以.(2)由题意知，.Y的可能取值为，所以，所以.所以，令，解得.所以当时，；当时，；当时，.【例3】2022北京冬奥会和冬残奥会吉祥物冰墩墩、雪容融亮相上海展览中心．为了庆祝吉祥物在上海的亮相，某商场举办了一场赢取吉祥物挂件的“定点投篮”活动，方案如下：方案一：共投9次，每次投中得1分，否则得0分，累计所得分数记为；方案二：共进行三轮投篮，每轮最多投三次，直到投中两球为止得3分，否则得0分，三轮累计所得分数记为．累计所得分数越多，所获得奖品越多．现在甲准备参加这个“定点投篮”活动，已知甲每次投篮的命中率为，每次投篮互不影响．(1)若，甲选择方案二，求第一轮投篮结束时，甲得3分的概率；(2)以最终累计得分的期望值为决策依据，甲在方案一，方案二之中选其一，应选择哪个方案？【答案】(1)；(2)答案见解析.【分析】（1）根据给定条件，将甲得3分的事件分拆成两个互斥事件的和，再利用互斥事件的概率公式计算即可.（2）求出甲选方案一，方案二得分的期望，再比较大小作答.（1），甲选择方案二，甲得3分的事件是3次投篮，前两球投进与最后一次才投进第2球的事件和，所以，所以第一轮投篮结束时，甲得3分的概率为.（2）选方案一，则，选方案一得分的数学期望为，选方案二，每一轮得分只有0和3，能得3分的概率为，进行三轮投篮，得3分的次数为随机变量，则，，进行三轮总得分，则选择方案二得分的期望为，显然，当，，两种方案期望相同，所以选方案一，二都可以；    当，，方案二期望大，所以甲应该选方案二；    当，，方案一期望大，所以甲应该选方案一．【例4】某校从高三年级选拔一个班级代表学校参加“学习强国知识大赛”，经过层层选拔，甲、乙两个班级进入最后决赛，规定选手回答1道相关问题，根据最后的评判选择由哪个班级代表学校参加大赛．每个班级有5名选手，现从每个班级的5名选手中随机抽取3人回答这道问题．已知甲班的5人中只有3人可以正确回答这道题目，乙班的5人能正确回答这道题目的概率均为，甲、乙两个班每个人对问题的回答都是相互独立的．(1)求甲、乙两个班抽取的6人中至少有3人能正确回答这道题目的概率；(2)设甲班被抽取的选手中能正确回答题目的人数为X，求随机变量X的分布列与数学期望，并利用所学的知识分析由哪个班级代表学校参加大赛更好．【答案】(1)；(2)分布列见解析，，选择甲班代表学校参加比赛更好【分析】（1）利用对立事件：甲、乙两个班抽取的6人中有1人或2人能正确回答，利用超几何分布和二项分布运算求解；（2）利用超几何分布和二项分布求分别求期望和方差，分析理解判断．(1)设甲、乙两个班抽取的6人中至少有3人能正确回答这道问题为事件A由于甲班5人中有3人可以正确回答这道题目，故从甲班中抽取的3人中至少有1人能正确回答这道题目故事件为甲、乙两个班抽取的6人中有1人或2人能正确回答，具体情况为甲班1人回答正确，其他5人回答错误或甲班2人回答正确，其他4人回答错误或甲、乙两班各1人回答正确，其他4人回答错误因为所以(2)X的所有可能取值为1，2，3，，所以X的分布列为所以因为乙班能正确回答题目的人数，所以，即．因为，，，所以甲、乙两个班级能正确回答题目的人数的期望相等，但甲班的方差小于乙班，所以选择甲班代表学校参加比赛更好．【例5】为加强进口冷链食品监管，某省于2020年底在全省建立进口冷链食品集中监管专仓制度，在口岸、目的地市或县（区、市）等进口冷链食品第一入境点，设立进口冷链食品集中监管专仓，集中开展核酸检测和预防性全面消毒工作，为了进一步确定某批进口冷冻食品是否感染病毒，在入关检疫时需要对其采样进行化验，若结果呈阳性，则有该病毒；若结果呈阴性，则没有该病毒，对于份样本，有以下两种检验方式：一是逐份检验，则需检验n次：二是混合检验，将k份样本分别取样混合在一起，若检验结果为阴性，那么这k份全为阴性，因而检验一次就够了；如果检验结果为阳性，为了明确这k份究竟哪些为阳性，就需要对它们再次取样逐份检验，则k份检验的次数共为次若每份样本没有该病毒的概率为，而且样本之间是否有该病毒是相互独立的．(1)若，求2份样本混合的结果为阳性的概率．(2)若，取得4份样本，考虑以下两种检验方案：方案一：采用混合检验：方案二：平均分成两组，每组2份样本采用混合检验．若检验次数的期望值越小，则方案越“优”，试问方案一、二哪个更“优”？请说明理由．【答案】(1)；(2)方案一更“优”，理由见解析.【分析】（1）根据对立事件可得阳性的概率；（2）方案一的检验次数记为，则的可能取值为，，求出各自的概率，得出分布列和期望；方案二检验次数记为，则的可能取值为，，求出各自的概率，得出分布列和期望，比较可得结果．(1)该混合样本阴性的概率是，根据对立事件可得，阳性的概率为．(2)方案一：混在一起检验，方案一的检验次数记为，则的可能取值为，，；，其分布列为：则，方案二：由题意分析可知．每组份样本混合检验时，若阴性则检测次数为，概率为，若阳性，则检测次数为，概率为，方案二的检验次数记为，则的可能取值为，，．；；；其分布列为：则，，当时，可得，所以方案一更“优”【例6】甲、乙两个学校进行体育比赛，比赛共设三个项目，每个项目胜方得10分，负方得0分，没有平局．三个项目比赛结束后，总得分高的学校获得冠军．已知甲学校在三个项目中获胜的概率分别为0.5，0.4，0.8，各项目的比赛结果相互独立．(1)求甲学校获得冠军的概率；(2)用X表示乙学校的总得分，求X的分布列与期望．【答案】(1)；(2)分布列见解析，.【分析】（1）设甲在三个项目中获胜的事件依次记为，再根据甲获得冠军则至少获胜两个项目，利用互斥事件的概率加法公式以及相互独立事件的乘法公式即可求出；（2）依题可知，的可能取值为，再分别计算出对应的概率，列出分布列，即可求出期望．【详解】（1）设甲在三个项目中获胜的事件依次记为，所以甲学校获得冠军的概率为．（2）依题可知，的可能取值为，所以，,，，.即的分布列为期望.【例7】在某地区进行流行病学调查，随机调查了100位某种疾病患者的年龄，得到如下的样本数据的频率分布直方图：(1)估计该地区这种疾病患者的平均年龄（同一组中的数据用该组区间的中点值为代表）；(2)估计该地区一位这种疾病患者的年龄位于区间的概率；(3)已知该地区这种疾病的患病率为，该地区年龄位于区间的人口占该地区总人口的.从该地区中任选一人，若此人的年龄位于区间，求此人患这种疾病的概率．（以样本数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率，精确到0.0001）.【答案】(1)岁；(2)；(3)．【分析】（1）根据平均值等于各矩形的面积乘以对应区间的中点值的和即可求出；（2）设{一人患这种疾病的年龄在区间}，根据对立事件的概率公式即可解出；（3）根据条件概率公式即可求出．【详解】（1）平均年龄    （岁）．（2）设{一人患这种疾病的年龄在区间}，所以．（3）设“任选一人年龄位于区间[40,50)”，“从该地区中任选一人患这种疾病”，则由已知得：,则由条件概率公式可得从该地区中任选一人，若此人的年龄位于区间，此人患这种疾病的概率为．【例8】一种微生物群体可以经过自身繁殖不断生存下来，设一个这种微生物为第0代，经过一次繁殖后为第1代，再经过一次繁殖后为第2代……，该微生物每代繁殖的个数是相互独立的且有相同的分布列，设X表示1个微生物个体繁殖下一代的个数，．（1）已知，求；（2）设p表示该种微生物经过多代繁殖后临近灭绝的概率，p是关于x的方程：的一个最小正实根，求证：当时，，当时，；（3）根据你的理解说明（2）问结论的实际含义．【答案】（1）1；（2）见解析；（3）见解析.【分析】（1）利用公式计算可得.（2）利用导数讨论函数的单调性，结合及极值点的范围可得的最小正零点.（3）利用期望的意义及根的范围可得相应的理解说明.【详解】（1）.（2）设，因为，故，若，则，故.，因为，，故有两个不同零点，且，且时，；时，；故在，上为增函数，在上为减函数，若，因为在为增函数且，而当时，因为在上为减函数，故，故为的一个最小正实根，若，因为且在上为减函数，故1为的一个最小正实根，综上，若，则.若，则，故.此时，，故有两个不同零点，且，且时，；时，；故在，上为增函数，在上为减函数，而，故，又，故在存在一个零点，且.所以为的一个最小正实根，此时，故当时，.（3）意义：每一个该种微生物繁殖后代的平均数不超过1，则若干代必然灭绝，若繁殖后代的平均数超过1，则若干代后被灭绝的概率小于1.【例9】在核酸检测中, “k合1” 混采核酸检测是指：先将k个人的样本混合在一起进行1次检测,如果这k个人都没有感染新冠病毒，则检测结果为阴性，得到每人的检测结果都为阴性，检测结束:如果这k个人中有人感染新冠病毒，则检测结果为阳性，此时需对每人再进行1次检测,得到每人的检测结果，检测结束.现对100人进行核酸检测，假设其中只有2人感染新冠病毒，并假设每次检测结果准确.（I）将这100人随机分成10组，每组10人，且对每组都采用“10合1”混采核酸检测.(i)如果感染新冠病毒的2人在同一组，求检测的总次数;(ii)已知感染新冠病毒的2人分在同一组的概率为.设X是检测的总次数，求X的分布列与数学期望E(X).(II）将这100人随机分成20组，每组5人，且对每组都采用“5合1”混采核酸检测.设Y是检测的总次数，试判断数学期望E(Y)与(I)中E(X)的大小.(结论不要求证明)【答案】（1）①次；②分布列见解析；期望为；（2）．【分析】（1）①由题设条件还原情境，即可得解；②求出X的取值情况，求出各情况下的概率，进而可得分布列，再由期望的公式即可得解；（2）求出两名感染者在一组的概率，进而求出，即可得解.【详解】（1）①对每组进行检测，需要10次；再对结果为阳性的组每个人进行检测，需要10次；所以总检测次数为20次；②由题意，可以取20，30，，，则的分布列:所以；（2）由题意，可以取25，30，两名感染者在同一组的概率为，不在同一组的概率为，则.【例10】某企业准备投产一批特殊型号的产品，已知该种产品的总成本与产量的函数关系式为，该种产品的市场前景无法确定，有三种可能出现的情况，各种情形发生的概率及产品价格与产量的函数关系式如下表所示:设分别表示市场情形好、中、差时的利润，随机变量，表示当产量为，而市场前景无法确定时的利润.试求:（1）分别求利润与产量的函数关系式;（2）当产量确定时，求期望;（3）试问产量取何值时，取得最大值.【答案】（1）；；；（2），；（3）时，取得最大值.【分析】（1）利用“利润=价格产量总成本”计算利润即可；（2）利用期望定义计算即可；（3）设函数，先求导数，再利用导数的正负研究函数的单调性，即得当时，取得最大值，即得结果.【详解】解:（1）由题意可得，L1=，，同理可得， ，，；（2）由期望定义可知，，；（3）由(2)可知，是产量 q的函数，设， ，得，令 解得 (舍去).故当时，；当 时，；可知，当时，取得最大值，即最大时产量.【例11】现有甲、乙两个项目，对甲项目每投资10万元，一年后利润是1.2万元、1.18万元、1.17万元的概率分别为；已知乙项目的利润与产品价格的调整有关，在每次调整中，价格下降的概率都是p(01.18，整理得(p＋0.4)(p－0.3)<0，解得－0.4