数学必修 第二册8.1 基本立体图形当堂检测题

这是一份数学必修 第二册8.1 基本立体图形当堂检测题，共14页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．有下列命题，其中错误命题个数是（ ）
①圆柱是将矩形旋转一周所得的几何体；②过圆锥顶点的截面是等腰三角形；③以直角三角形一边为旋转轴，旋转所得的旋转体是圆锥；④平行于母线的平面截圆锥，截面是等腰三角形.
A．1个B．2个C．3个D．4个
2．圆柱内有一内接正三棱锥，过棱锥的一条侧棱和高作截面，正确的截面图是（ ）
A．B．
C．D．
3．圆柱的侧面展开图是一个正方形，则它的母线长和底面半径的比值是（ ）
A．1B．2C．D．
4．长方体中，，，则此长方体的对角线长是（ ）
A．2B．C．D．
5．若正方体的一个截面恰好截这个正方体为等体积的两部分，则该截面( )
A．一定通过正方体的中心B．一定通过正方体一个表面的中心
C．一定通过正方体的一个顶点D．一定构成正多边形
6．若一个棱锥的每条侧棱在底面的射影长相等，则此棱锥（ ）
A．是正四面体B．是正棱锥C．不是正棱锥D．不一定是正棱锥
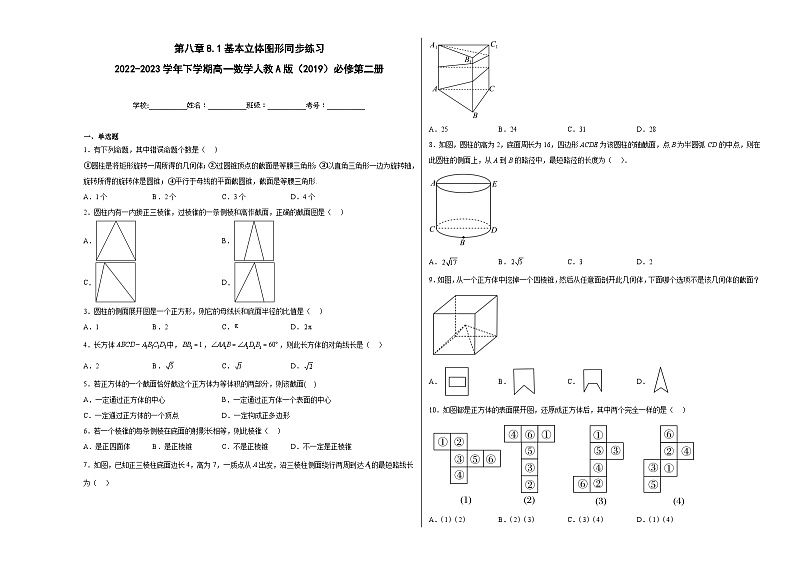
7．如图，已知正三棱柱底面边长4，高为7，一质点从A出发，沿三棱柱侧面绕行两周到达的最短路线长为（ ）
A．25B．24C．31D．28
8．如图，圆柱的高为2，底面周长为16，四边形ACDE为该圆柱的轴截面，点B为半圆弧CD的中点，则在此圆柱的侧面上，从A到B的路径中，最短路径的长度为（ ）．
A．B．C．3D．2
9．如图，从一个正方体中挖掉一个四棱锥，然后从任意面剖开此几何体，下面哪个选项不是该几何体的截面？
A．B．C．D．
10．如图都是正方体的表面展开图，还原成正方体后，其中两个完全一样的是（ ）
A．（1）（2）B．（2）（3）C．（3）（4）D．（1）（4）
11．一个正方体内有一个内切球，作正方体的对角面，所得的截面图形是（ ）
A．B．C．D．
12．给出下列命题：①用平行于底面的平面截棱锥所得的截面与底面相似；②两底面平行，各侧面都是梯形的空间图形是棱台；③棱柱的侧面展开后是一个平行四边形或矩形．其中正确的个数是（ ）
A．0B．1C．2D．3
13．若一个圆锥的轴截面是面积为9的等腰直角三角形，则这个圆锥的底面半径为（ ）
A．1B．2C．3D．4
14．下列平面图形中，绕轴旋转一周得到如图所示的空间图形的是（ ）
A．B．C．D．
15．下列说法中正确的是（ ）
A．球的半径可以是球面上任意一点与球心所连的线段
B．球的直径可以是球面上任意两点所连的线段
C．用一个平面截球，得到的截面可以是正方形
D．球不可以用表示球心的字母表示
二、填空题
16．长、宽、高分别为3、4，5的两个相同的长方体，把它们某两个全等的面重合在一起，组成大长方体，则大长方体对角线最长为_____.
17．在正方体中，棱长为2，E为的中点，点P在平面内运动，则的最小值为________
18．若圆锥的轴截面是边长为2的等边三角形，则该圆锥顶点到底面的距离为______.
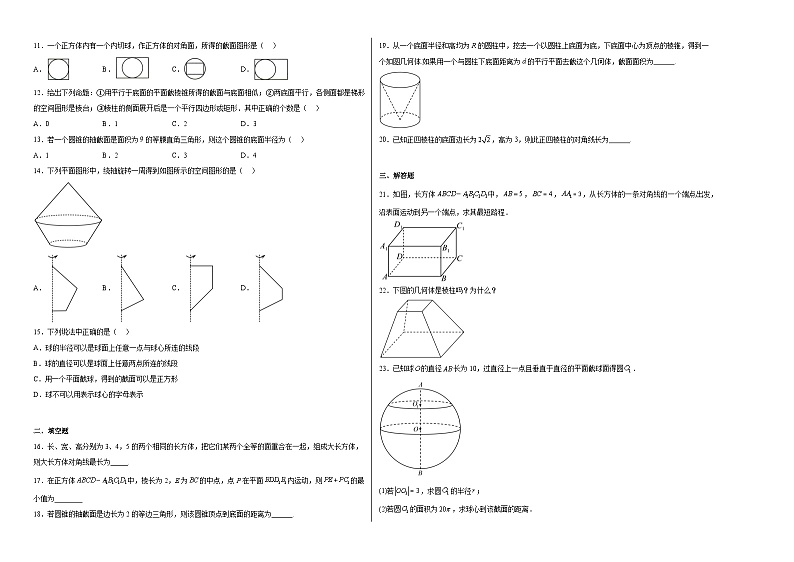
19．从一个底面半径和高均为R的圆柱中，挖去一个以圆柱上底面为底，下底面中心为顶点的棱锥，得到一个如图几何体.如果用一个与圆柱下底面距离为d的平行平面去截这个几何体，截面面积为______.
20．已知正四棱柱的底面边长为，高为3，则此正四棱柱的对角线长为______.
三、解答题
21．如图，长方体中，，，，从长方体的一条对角线的一个端点出发，沿表面运动到另一个端点，求其最短路程．
22．下图的几何体是棱柱吗？为什么？
23．已知球的直径长为10，过直径上一点且垂直于直径的平面截球面得圆．
(1)若，求圆的半径；
(2)若圆的面积为，求球心到该截面的距离．
24．用一个平行于圆锥底面的平面截这个圆锥，截得的两个几何体分别为一个小圆锥和一个圆台，若小圆锥的母线与圆台的母线之比为3：1，圆台的上底面半径为3cm，求圆台的下底面面积.
参考答案：
1．C
【分析】由圆柱、圆锥的结构特征逐一分析四个命题得结论．
【详解】解：①圆柱是将矩形以一边为轴旋转一周所得的几何体，故①错误；
②过圆锥顶点的截面是等腰三角形，故②正确；
③以直角三角形一直角边为旋转轴，旋转所得的旋转体是圆锥，故③错误；
④平行于母线的平面截圆锥，截面不是等腰三角形，是抛物线，故④错误．
其中错误命题个数为3．
故选：C．
2．D
【分析】根据截面在圆柱底面所形成的截痕直接判断即可.
【详解】圆柱底面为正三棱锥底面三角形的外接圆，如下图所示，
则过棱锥的一条侧棱和高作截面，棱锥顶点为圆柱上底面的中心，可得截面图如下图，
故选：D.
3．D
【分析】设圆柱母线、半径，结合即可得结果.
【详解】令圆柱母线为，底面半径为，则，故.
故选：D
4．B
【分析】根据题意，作图，根据勾股定理和锐角三角函数，分别计算出长方形的长宽高，进而利用长方体的对角线的计算公式，直接计算可得答案
【详解】
由已知得，，，根据勾股定理和锐角三角函数，在直角三角形中，得，，在直角三角形中，由，可得，，则此长方体的对角线长为.
故选：B
5．A
【分析】根据正方体的性质，所有过中心的截面都把正方体分成体积相等的两部分，从而可得正确答案．
【详解】根据题意，恰好截正方体为等体积的两部分的截面，可能为中截面、对角面、也可能是倾斜的平面，不管哪种截面都过正方体的中心．
故选：A．
6．D
【分析】根据题意可判断棱锥的底面不一定是正多边形，故可判断棱锥的形状，可得答案.
【详解】若一个棱锥的每条侧棱在底面的射影长相等,则顶点在底面上的射影为底面多边形的外心，
但底面不一定是正多边形，故此棱锥不一定是正棱锥，
故选：D
7．A
【分析】根据正三棱柱的侧面展开图求得最短线路长.
【详解】正三棱柱的侧面展开图是底边长为，高为的矩形，
所以绕行两周的最短路线长为.
故选：A
8．B
【分析】画出圆柱的侧面展开图，解三角形即得解.
【详解】解：圆柱的侧面展开图如图所示，由题得,
所以.
所以在此圆柱的侧面上，从A到B的路径中，最短路径的长度为.
故选：B
9．A
【分析】可通过确定截面的不同位置去剖开正方体，想象相对应的截面形状，即可确定答案.
【详解】对于A，由于截面中间是矩形，如果可能的话，一定是用和正方体底面平行的截面去剖开
正方体并且是从挖去四棱锥的那部分剖开，但此时剖面中间应该是一个正方形，
因此A图形不可能是截面；
对于B，当从正方体底面的一组相对棱的中点处剖开时，截面正好通过四棱锥顶点，
如图：
此时截面形状如B图形，故B可能是该几何体的截面；
对于C,当截面不经过底面一组相对棱的中点处，并和另一组棱平行去剖开正方体时，
如图中截面PDGH位置：
截面就会如C图形，故C可能是该几何体的截面；
对于D，如图示，按图中截面 的位置去剖开正方体，截面就会如D图形，
故D可能是该几何体的截面；
故答案为：A
10．B
【分析】分别判断出还原成正方体后，相对面的标号，即可得出答案．
【详解】（1）图还原正方体后，①⑤对面，②④对面，③⑥对面；
（2）图还原后，①④对面，②⑤对面，③⑥对面；
（3）图还原后，①④对面，②⑤对面，③⑥对面；
（4）图还原后，①⑥对面，②⑤对面，③④对面；
综上可得，还原成正方体后，正方体完全一样的是（2）（3）．
故选：B．
11．B
【分析】由对角线组成的面称为对角面，易得正方体的对角面是一个矩形，而球截面在矩形正中间，与矩形的两条边相切，据此即可判断
【详解】由组合体的结构特征可知球与正方体的各面相切，而与各棱相离，所以截面图形中的圆与上下底面的对角线相切，与两侧棱相离，只有B符合
故选：B
12．B
【分析】根据棱锥的截面、棱台、棱柱的侧面展开图等知识对三个命题进行分析，从而确定正确答案.
【详解】①，用平行于底面的平面截棱锥所得的截面与底面相似，①正确；
②，符合命题的空间图形的侧棱未必交于一点，故②错误；
③，斜棱柱的侧面展开后可能是多边形的组合图形，故③错误．
故正确的有个.
故选：B
13．C
【分析】设底面半径为r，利用轴截面的面积列方程求出r的值.
【详解】设底面半径为r．因为轴截面是等腰直角三角形，所以圆锥的高也是r．
据题意得，解得．
故选：C.
14．A
【分析】题图中的空间图形是一个圆锥和一个圆台的组合体，再结合圆锥和圆台的形成过程即可得出答案.
【详解】题图中的空间图形是一个圆锥和一个圆台的组合体．
圆台是由直角梯形以为旋转轴，其余各边旋转而形成的曲面所围成的几何体，
圆锥是由直角三角形以为旋转轴，其余两边旋转而成的曲面所围成的几何体.

故选：A.
15．A
【分析】根据球的定义及性质，逐项判断即可.
【详解】解：根据球的定义知A正确；
因为球的直径必过球心，所以B错误；
因为球的任何截面都是圆面，所以C错误；
球常用表示球心的字母表示，故D错误.
故选：A.
16．
【分析】分类讨论求解大长方体的体对角线即可.
【详解】当大长方体的长、宽、高分别为、、时，
体对角线为.
当大长方体的长、宽、高分别为、、时，
体对角线为.
当大长方体的长、宽、高分别为、、时，
体对角线为.
因为，所以大长方体对角线最长为.
故答案为：
17．3
【分析】由条件证明点E、F关于平面对称，由此可得，再根据结论两点之间线段最短求的最小值即可.
【详解】取的中点F，连接，如下图：
因为E为的中点，所以点E、F关于平面对称，
所以，
因为，
当且仅当点为线段与平面的交点时等号成立；
所以的最小值为，
由已知为直角三角形，且，为直角，
所以，
所以的最小值为3.
故答案为：3.
18．
【分析】画出圆锥图像，根据题意顶点到底面的距离即圆锥的高，在直角三角形中即可解决.
【详解】如图所示，
是边长为2的等边三角形，
该圆锥顶点到底面的距离为.
故答案为：
19．
【分析】作出如图所示的轴截面，根据平面几何关系即可得解.
【详解】解：如图所示作出轴截面，
圆柱被平行于下底面的平面所截得的截面圆的半径，
设圆锥的截面圆的半径为，
因为，所以是等腰直角三角形.
又，所以，故，
所以截面积.
故答案为：.
20．5
【分析】求出底面正方形对角线长，由勾股定理计算四棱柱的对角线长（需证明垂直）．
【详解】如图正四棱柱中，底面是正方形，与底面垂直，则与底面上的直线垂直，
由已知，又，所以．
故答案为：5.
21．
【分析】把长方体的面展开，计算展开图中从到距离，不同的展开方式，可以有三种不同的结果，比较大小，得到最短路径.
【详解】选择从长方体的点出发，沿表面运动到点.
长方体的表面可以有如下三种展开方式，到两点的距离分别是：
如图1，；如图2，；
如图3，.
因为，
所以其最短路程为.
22．不是，理由见解析
【分析】由棱柱的定义判断
【详解】不是，根据棱柱的定义，应有两个全等的互相平行的平面多边形，图中几何体没有.
23．(1)4
(2)
【分析】（1）利用勾股定理计算可得；
（2）记圆的半径为，球心到该截面的距离为，由截面圆的面积求出，再由计算可得；
（1）
解：因为球的半径，所以．
（2）
解：记圆的半径为，球心到该截面的距离为，
则，得，
因此．
24．
【分析】根据三角形相似即可得下底面圆的半径，进而可求圆的面积.
【详解】如图，设PA为大圆锥的一条母线，
过PA和 的平面与两个圆锥的底面的交线分别为和，则由两个平面平行的性质定理，知，所以，
所以，
由题意，得，则，
所以，所以圆台的下底面面积为.