人教A版 (2019)必修 第二册8.5 空间直线、平面的平行当堂达标检测题

这是一份人教A版 (2019)必修 第二册8.5 空间直线、平面的平行当堂达标检测题，共20页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


学校:___________姓名：___________班级：___________考号：___________
一、单选题
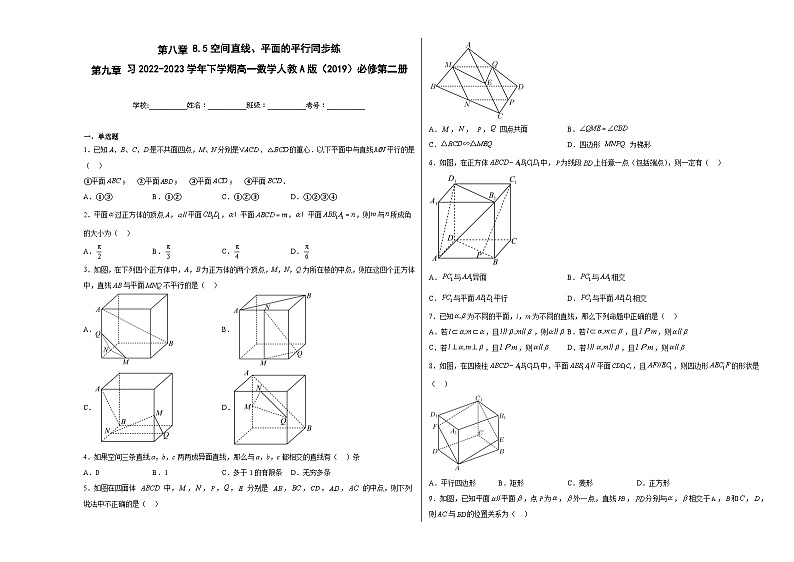
1．已知A、B、C、D是不共面四点，M、N分别是、的重心．以下平面中与直线平行的是（ ）
①平面； ②平面； ③平面； ④平面．
A．①③B．①②C．①②③D．①②③④
2．平面过正方体的顶点A，平面，平面，平面，则与所成角的大小为（ ）
A．B．C．D．
3．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是（ ）
A．B．
C．D．
4．如果空间三条直线a，b，c两两成异面直线，那么与a，b，c都相交的直线有（ ）条
A．0B．1C．多于1的有限条D．无穷多条
5．如图在四面体 中，，，，， 分别是 ，，，， 的中点，则下列说法中不正确的是（ ）
A．，， ， 四点共面B．
C． D．四边形 为梯形
6．如图，在正方体中，为线段上任意一点（包括端点），则一定有（ ）
A．与异面B．与相交
C．与平面平行D．与平面相交
7．已知为不同的平面，l，m为不同的直线，那么下列命题中正确的是（ ）
A．若，且，则B．若，且，则
C．若，且，则D．若，且，则
8．如图，在四棱柱中，平面平面，且，则四边形的形状是（ ）
A．平行四边形B．矩形C．菱形D．正方形
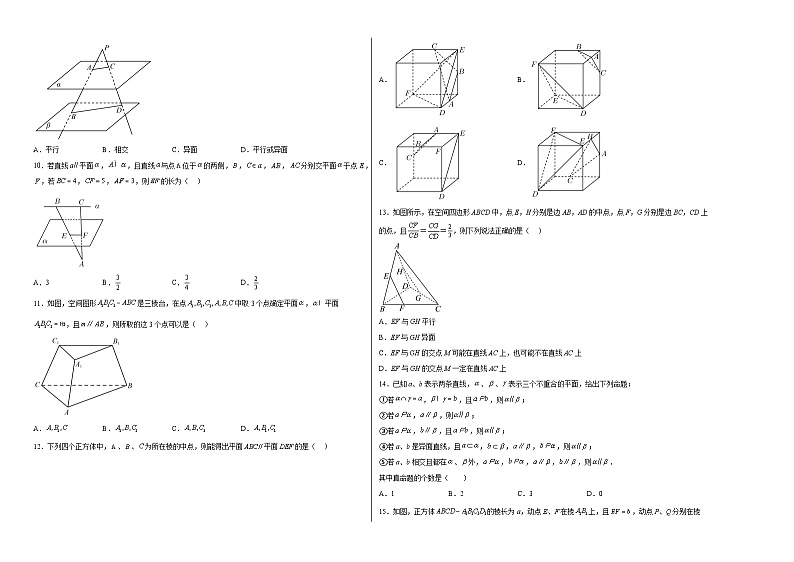
9．如图，已知平面平面，点为，外一点，直线，分别与，相交于，和，，则与的位置关系为（ ）
A．平行B．相交C．异面D．平行或异面
10．若直线平面，，且直线与点位于的两侧，，，，分别交平面于点，，若，，，则的长为（ ）
A．3B．C．D．
11．如图，空间图形是三棱台，在点中取3个点确定平面，平面，且，则所取的这3个点可以是（ ）
A．B．C．D．
12．下列四个正方体中，、、为所在棱的中点，则能得出平面平面的是（ ）
A．B．
C．D．
13．如图所示，在空间四边形ABCD中，点E，H分别是边AB，AD的中点，点F，G分别是边BC，CD上的点，且＝＝，则下列说法正确的是（ ）
A．EF与GH平行
B．EF与GH异面
C．EF与GH的交点M可能在直线AC上，也可能不在直线AC上
D．EF与GH的交点M一定在直线AC上
14．已知a、b表示两条直线，、、表示三个不重合的平面，给出下列命题：
①若，，且，则；
②若，，则；
③若，，且，则；
④若a、b是异面直线，且，，，，则；
⑤若a、b相交且都在、外，，，，，则．
其中真命题的个数是（ ）
A．1B．2C．3D．0
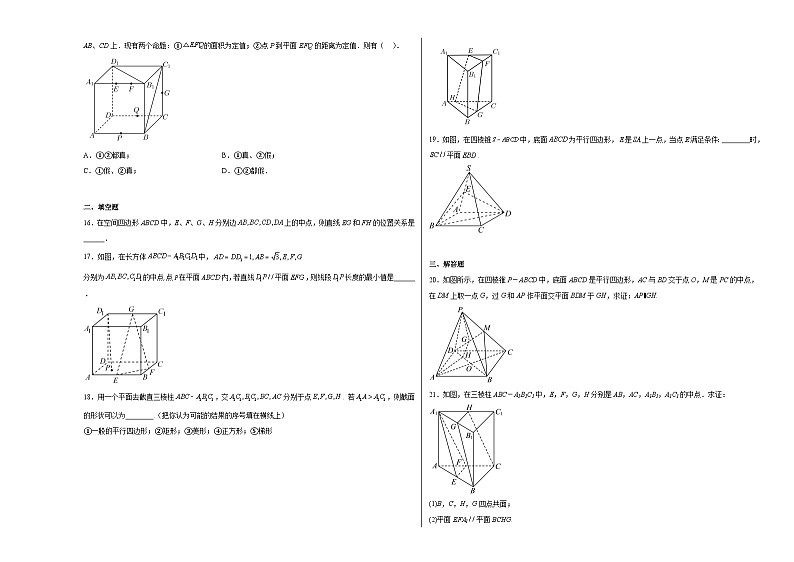
15．如图，正方体的棱长为a，动点E、F在棱上，且，动点P、Q分别在棱AB、CD上．现有两个命题：①的面积为定值；②点P到平面EFQ的距离为定值．则有（ ）．
A．①②都真；B．①真、②假；
C．①假、②真；D．①②都假．
二、填空题
16．在空间四边形ABCD中，E、F、G、H分别边上的中点，则直线EG和FH的位置关系是______．
17．如图，在长方体中，
分别为的中点.点在平面内，若直线平面，则线段长度的最小值是______・
18．用一个平面去截直三棱柱，交分别于点. 若，则截面的形状可以为________.（把你认为可能的结果的序号填在横线上）
①一般的平行四边形；②矩形；③菱形；④正方形；⑤梯形
19．如图，在四棱锥中，底面为平行四边形，是上一点，当点满足条件：________时，平面.
三、解答题
20．如图所示，在四棱锥P－ABCD中，底面ABCD是平行四边形，AC与BD交于点O，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH，求证：AP∥GH.
21．如图，在三棱柱ABC－A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点．求证：
(1)B，C，H，G四点共面；
(2)平面EFA1平面BCHG.
22．长方体中，是矩形的中心，是矩形的中心．证明：平面.
23．在正方体中．为底面中心，为中点，为中点．证明：平面平面PAO．
参考答案：
1．B
【分析】由已知以及重心定理可推得，进而得到，根据线面平行的判定定理可得①②正确；进而可判断直线与平面以及平面相交，即可得出③④错误.
【详解】
如图，取中点为，连结、.
由已知以及重心定理可得，，，则，.
所以，所以.
因为平面，平面，所以平面，故①正确；
因为平面，平面，所以平面，故②正确；
因为平面，平面，所以与平面不平行，故③错误；
因为平面，平面，所以与平面不平行，故④错误.
故选：B.
2．B
【分析】根据面面平行的性质，判断直线与所成的角，通过解三角形即可求解.
【详解】如图：因为平面，平面平面，
平面，平面平面，所以．
因为平面，平面平面，
平面，平面平面，所以．
所以与所成角的大小等于与所成角的大小，即为所求．
因为为正三角形，所以，即m与n所成角的大小为．
故选：.
3．A
【分析】利用线面平行判定定理可知B，C，D均不满足题意，A选项可证明出直线AB与平面MNQ不平行，从而可得答案.
【详解】对于选项B，如图1，连接CD，
因为M，N，Q为所在棱的中点，所以CDMQ，
由于ABCD，所以ABMQ，
因为平面，平面，所以AB平面MNQ，
B选项不满足题意；
对于选项C，如图2，连接CD，
因为M，N，Q为所在棱的中点，所以CDMQ，
由于ABCD，所以ABMQ，
因为平面，平面，所以AB平面MNQ，
C选项不满足题意；
对于选项D，如图3，连接CD，
因为M，N，Q为所在棱的中点，所以CDNQ，
由于ABCD，所以ABNQ，
因为平面，平面，所以AB平面MNQ，
可知D不满足题意；
如图4，取BC的中点D，连接QD，
因为Q是AC的中点，
所以QDAB，
由于QD与平面MNQ相交，故AB与平面MNQ不平行，
A正确.
故选：A
4．D
【分析】在三条直线上取三条线段作一个平行六面体，由上取一点，过作一平面，与交于，由面面平行的性质和平行线的性质得到与相交，所以是与都相交的一条直线，最后根据点的任意性得出结论.
【详解】在直线上取三条线段，作一个平行六面体，
如下图所示，
在上，也即在上任取一点，过作一平面，
平面与交于，与交于，则由面面平行的性质定理可得：，
于是不与平行，但与共面，故与相交，所以是与都相交的一条直线，
由点的任意性可知：与都相交的直线有无穷多条，
故选：.
5．D
【分析】利用中位线定理和等角定理即可解决.
【详解】由图可知，在中，,,分别是 ,的中点，
所以 且，
同理在中， 且，
所以所以四边形为平行四边形，
所以，， ， 四点共面，所以A正确;
在中,由中位线定理得
同理在中，由中位线定理得,
所以由等角定理知，，所以B正确;
在中，由中位线定理得
所以,
所以由等角定理可知，
，,,
所以，所以C正确;
由上述分析得四边形为平行四边形，所以D错误;
故选:D.
6．C
【分析】连接、、、，证明出四边形为平行四边形，并结合面面平行的性质可判断各选项能否一定成立.
【详解】连接、，因为且，所以，四边形为平行四边形，
当为、的交点时，与相交，
当不为、的交点时，与异面，AB选项都不一定成立；
连接、，因为且，故四边形为平行四边形，
，平面，平面，平面，
同理可证平面，
因为，、平面，平面平面，
平面，平面，C选项一定满足，D选项一定不满足.
故选：C.
7．C
【分析】利用直线、平面的位置关系以及平行的传递性进行判断.
【详解】对于选项A，如图，若，且，但，故A错误.
对于选项B，如图，，且，但，故B错误.
对于选项C，如图，根据平行的传递性，若，且，则，
故C正确.
对于选项D，如图，，且，但，故D错误.
故选：C.
8．A
【分析】根据平行关系可知四点共面，由面面平行的性质可证得，由此可得结论.
【详解】，四点共面；
平面平面，平面平面，平面平面，，
四边形为平行四边形.
故选：A.
9．A
【分析】由题设知，，，，共面，根据面面平行的性质，可证与的位置关系.
【详解】解：由题意知，，，，在同一平面内，且平面平面，平面平面，且，∴，
故选：A．
10．B
【分析】根据线面平行可得线线平行，从而可求.
【详解】∵，平面，平面，
∴，∴，即，∴.
故选：B.
11．C
【分析】根据面面平行的性质定理即可判断.
【详解】解：由空间图形是三棱台，可得平面平面，
当平面为平面，平面平面时，又平面平面，
所以由面面平行的性质定理可知，所以选项C符合要求.
故选：C．
12．B
【分析】利用反证法可判断A选项；利用面面平行的判定定理可判断B选项；利用反证法结合面面平行的性质可判断C选项；利用面面平行的判定和性质定理、结合反证法可判断D选项.
【详解】对于A选项，若平面平面，平面，则平面，
由图可知与平面相交，故平面与平面不平行，A不满足条件；
对于B选项，如下图所示，连接，
因为、分别为、的中点，则，
在正方体中，且，
故四边形为平行四边形，所以，，，
平面，平面，平面，
同理可证平面，，因此，平面平面，B满足条件；
对于C选项，如下图所示：
在正方体中，若平面平面，且平面平面，
则平面平面，但这与平面与平面相交矛盾，
因此，平面与平面不平行，C不满足条件；
对于D选项，在正方体中，连接、、，如下图所示：
因为且，则四边形为平行四边形，则，
平面，平面，所以，平面，
同理可证平面，，所以，平面平面，
若平面平面，则平面平面，
这与平面与平面相交矛盾，故平面与平面不平行，D不满足条件.
故选：B.
13．D
【分析】连接EH，FG，根据F，G分别是边BC，CD上的点，且＝＝，和点E，H分别是边AB，AD的中点，得到EH//GF，且EH≠GF判断.
【详解】解：如图所示：
连接EH，FG.
因为F，G分别是边BC，CD上的点，且＝＝，
所以GF//BD，且GF＝BD.
因为点E，H分别是边AB，AD的中点，
所以EH//BD，且EH＝BD，
所以EH//GF，且EH≠GF，
所以EF与GH相交，设其交点为M，
则M∈平面ABC，同理M∈平面ACD.
又平面ABC∩平面ACD＝AC，
所以M在直线AC上．
故选：D.
14．B
【分析】直接由面面平行的判定依次判断5个命题即可.
【详解】对于①，若，，且，则相交或平行，故①错误；
对于②，若，，则相交或平行，故②错误；
对于③，若，，且，则相交或平行，故③错误；
对于④，若相交，设，则由可得，由可得，故，与a、b是异面直线矛盾，故，④正确；
对于⑤，由，可得所在平面平行于，同理可得所在平面平行于，故，⑤正确.
故选：B.
15．A
【分析】根据线线平行和线面平行的判定定理与性质依次判断命题即可.
【详解】对于①，因为，所以Q到直线的距离h为定值，
而EF为定值，故的面积为定值，所以①真．
对于②，因为，平面EFQ，所以平面EFQ，
故点P到平面EFQ的距离为定值，所以②真．
故选：A
16．相交
【分析】根据平面的性质结合线线位置关系分析判断.
【详解】∵E、F、G、H分别是四边上的中点，
∴，即，
同理可得：，
故E、F、G、H四点共面，且为平行四边形，则直线EG和FH的位置关系是相交.
故答案为：相交.
17．
【分析】利用线面平行的判定定理，面面平行的判定定理，确定在直线，再根据时线段最短即可求解.
【详解】解：如图，连结，
∵分别为的中点，
∴平面，平面，
∴平面
∵平面，平面，
∴平面，
∵，∴平面平面，
∵平面，
∴点在直线上，在中，，
∴当时，线段的长度最小，最小值为＝.
故答案为：.
18．②④⑤
【分析】由面面可得截面交线，进一步对与平行与否进行讨论即可.
【详解】为直三棱柱，则面面，截面过面、面，则交线，
当不与平行时，此时截得的EH不平行于FG，四边形为梯形；
当时，此时截得的，，
当时，四边形为矩形；当时，四边形为正方形；
故答案为：②④⑤
19．答案表述不唯一)
【分析】当为的中点，为的中点时，根据三角形中位线的性质即可判断，从而可得平面，由此可得出点满足条件的结论.
【详解】连接交于O，连接OE，
平面平面，平面平面 ，
.
又 底面为平行四边形，为对角线与的交点，
故为的中点, 为的中点，
故当满足条件: 时，面.
故答案为: 答案表述不唯一)
20．证明见解析
【分析】先证明线面平行，由AP∥平面BDM的性质可得AP∥GH.
【详解】证明 如图，连接MO.
∵四边形ABCD是平行四边形，
∴O是AC的中点．
又∵M是PC的中点，∴AP∥OM.
又∵AP⊄平面BDM，
OM⊂平面BDM，
∴AP∥平面BDM.
又∵AP⊂平面APGH，平面APGH∩平面BDM＝GH，
∴AP∥GH.
21．(1)证明见解析
(2)证明见解析
【分析】（1）利用中位线定理与空间平行线的传递性，推得，由此得证；
（2）利用线面平行的判定定理证得EF平面BCHG，A1E平面BCHG，从而利用面面平行的判定定理即可得证.
【详解】（1）∵G，H分别是A1B1，A1C1的中点
∴GH是的中位线，∴GHB1C1，
又在三棱柱ABC－A1B1C1中，B1C1BC，∴GHBC，
∴B，C，H，G四点共面．
（2）∵E，F分别为AB，AC的中点，
∴EFBC，
∵平面BCHG，BC⊂平面BCHG，
∴EF平面BCHG，
∵在三棱柱ABC－A1B1C1中，，，
∴A1GEB，，
∴四边形A1EBG是平行四边形，∴A1EGB，
∵平面BCHG，GB⊂平面BCHG，
∴A1E平面BCHG，
∵A1E∩EF＝E，A1E，EF⊂平面EFA1，
∴平面EFA1平面BCHG.
22．证明见详解
【分析】连结、、.由已知可推得，进而根据线面平行的判定定理，即可证明平面.
【详解】
证明：连结、、.
由已知可得，点是的中点，点是的中点，
所以，是的中位线，
所以.
又平面，平面，
所以平面.
23．证明见详解
【分析】根据线面、面面平行的判定定理分析证明.
【详解】由题意可得：分别为的中点，则，
平面，平面，
∴平面，
连接，由题意可得：分别为的中点，则，且，
∵，且，
则，且，
故为平行四边形，则，
平面，平面，
∴平面，
，平面，
故平面平面PAO.