人教A版 (2019)必修 第一册4.4 对数函数学案设计

这是一份人教A版 (2019)必修 第一册4.4 对数函数学案设计，共6页。学案主要包含了引入，探究归纳，对数函数性质的应用，走近高考，拓展延伸等内容，欢迎下载使用。

请在下面平面直角坐标系中画出函数y=lg2x和y=lg12x的图象
观察：函数y=lg2x和y=lg12x的图象关于 对称。
思考：底数互为倒数的两对数函数的图象是否也有相同关系？
结论：1.底数互为倒数的两对数函数图象关于 对称；
2.第一象限内，所有对数函数图象与直线y=m的交点位置与底
数大小的关系是 。
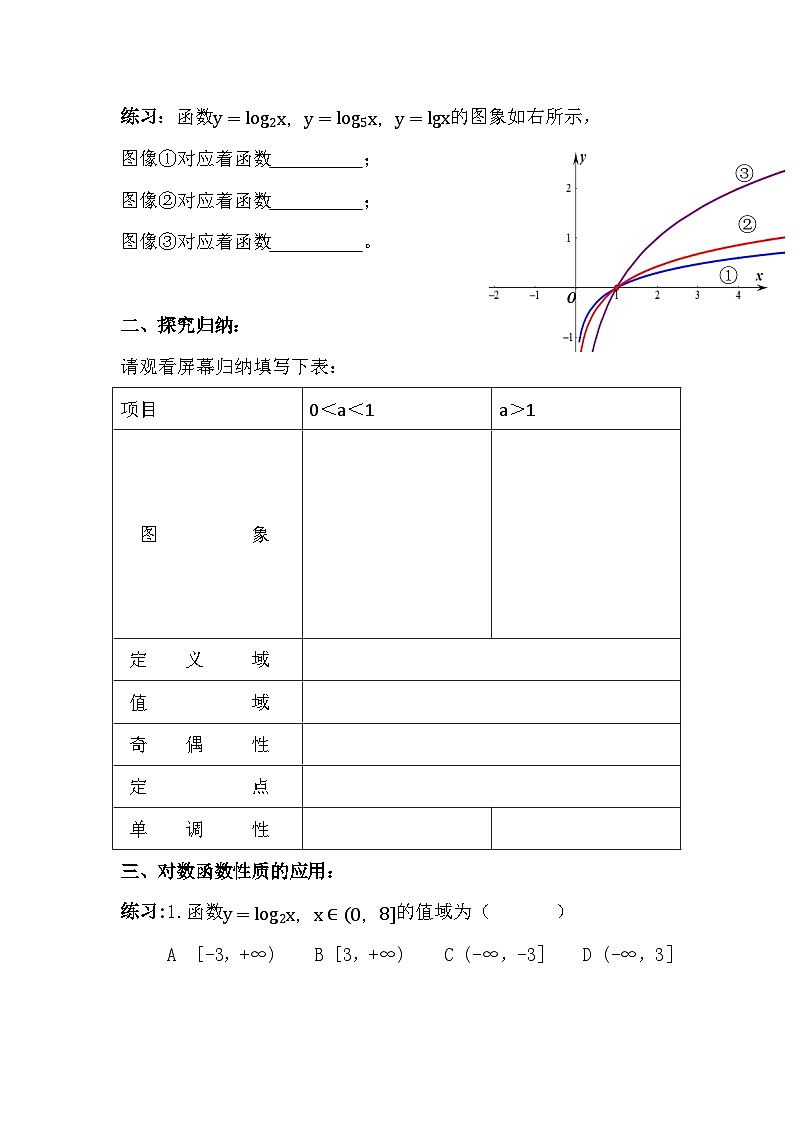
练习：函数y=lg2x，y=lg5x，y=lgx的图象如右所示，
③
图像①对应着函数 ；
②
图像②对应着函数 ；
①
图像③对应着函数 。
二、探究归纳：
请观看屏幕归纳填写下表：
三、对数函数性质的应用：
练习:1.函数y=lg2x，x∈0，8的值域为（ ）
A [-3，+∞) B [3，+∞) C (-∞，-3］ D (-∞，3］
2.请在横线上填写＞或＜：
（1）lg0.6 lg0.8；（2）lg0.56 lg0.54
例1.比较下列各题中两个值的大小：
（1）lgm5，lgm7（m＞0且m≠1）；
（2）lg26，lg36； （3）lg30.6，lg0.60.8
归纳：（1）两个同底对数比较大小的方法：
（2）两个同真数对数比较大小的方法：
（3）两个既不同底也不同真数的对数比较大小的方法：
例2. 已知lg0.7(2m)＜lg0.7(m-1)，求m的取值范围
四、走近高考：
1.（2021年全国II卷）已知a=lg52，b=lg83，c=12，则下列判断正确的是
A c＜b＜a B b＜a＜c C a＜c＜b D a＜b＜c
2.（2020全国III卷）设a=lg32，b=lg53，c=23，则
A a＜c＜b B a＜b＜c C b＜c＜a D c＜a＜b
五、拓展延伸：
1. 解下列不等式：
（1） （2）；
2. 若函数，则不等式的解集为 .
3.已知fx=3a−1x+2a，x≤1lgax，x>1是R上的单调递减函数，则实数a的取值范围是
A． B． C． D．
4. “x2-x-2＜0”是“lg2x＜1”的
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
5. y＝ax与y＝－lgax(a＞0，且a≠1)在同一坐标系中图象形状可能
6. 函数（且）的图象恒过点 ．
7. 函数，且的图象过定点 .
8. 函数（且）的图象恒过定点，若且，，则的最小值为（ ）
A．9B．8C．D．
9.已知函数，且．(1)求的定义域；
(2)当时，求关于x的不等式的解集．
拓展延伸答案：
1.（1）lg52−2，+∞；（2）3−lg36，+∞
2. 0，14∪2，+∞
3.C；
4.B；
5.A
6.(2,2)
7.(0,1)
8.B
9.（1）（-1,1）（2）（0,1）x
12
1
2
4
8
y=lg2x
y=lg12x
项目
0＜a＜1
a＞1
图 象
定 义 域

值 域
奇 偶 性
定 点
单 调 性