

还剩4页未读,
继续阅读
2023—2024学年人教版数学七年级下册5.2平行线及其判定同步练习(含答案)
展开
这是一份2023—2024学年人教版数学七年级下册5.2平行线及其判定同步练习(含答案),共7页。
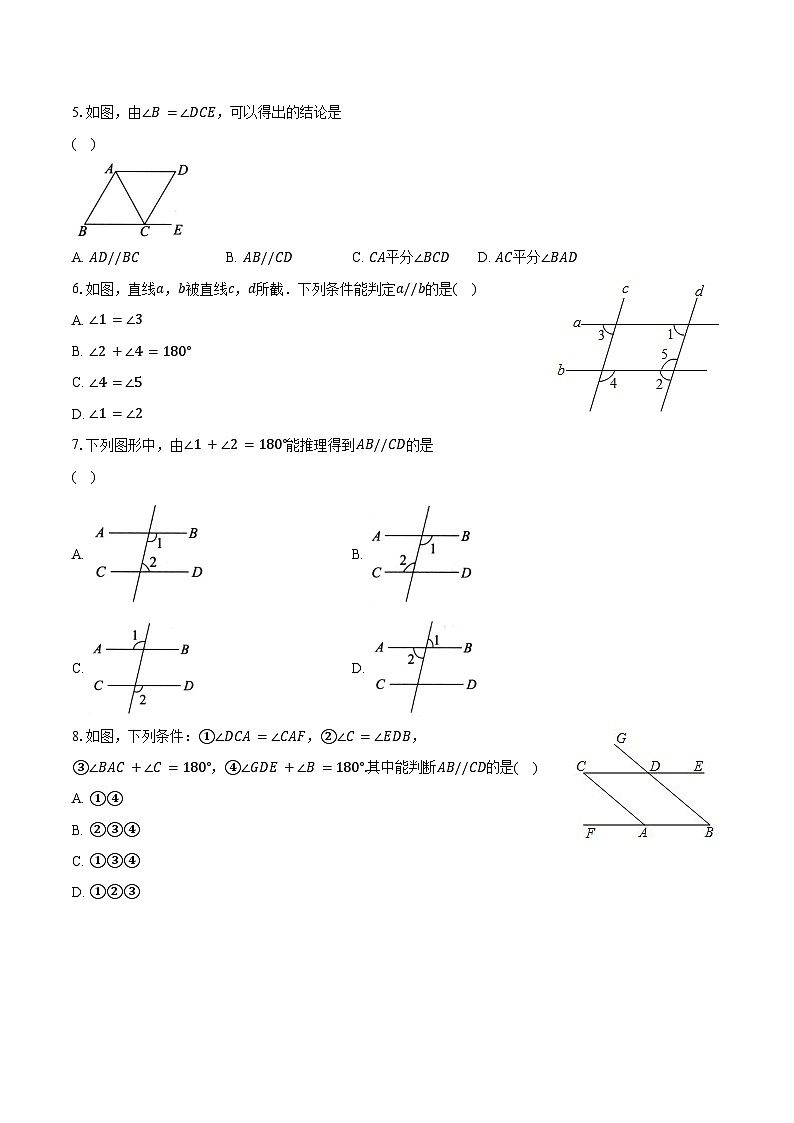
5.2平行线及其判定同步练习选择题:1.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出AB//DC的是( ) A. ①② B. ①③ C. ②③ D. ②④2.如图,下列推理不正确的是( ) A. 因为∠1=∠2,所以AE//BD B. 因为∠1=∠2,所以AB//ED C. 因为∠3=∠4,所以AB//CD D. 因为∠5=∠2+∠4,所以AE//BD3.(2023·贵阳期末)如图是小星探索两直线平行的条件时所用的学具,木条a,b,c在同一平面内,经测量∠1=65°,要使木条a//b,则∠2的度数应为 ( ) A. 25° B. 55° C. 65° D. 75°4.如图,过C点作直线AB的平行线,下列说法正确的是 ( ) A. 不能作 B. 只能作一条 C. 能作两条 D. 能作无数条5.如图,由∠B=∠DCE,可以得出的结论是 ( ) A. AD//BC B. AB//CD C. CA平分∠BCD D. AC平分∠BAD6.如图,直线a,b被直线c,d所截.下列条件能判定a//b的是( )A. ∠1=∠3 B. ∠2+∠4=180° C. ∠4=∠5 D. ∠1=∠27.下列图形中,由∠1+∠2=180°能推理得到AB//CD的是 ( )A. B. C. D. 8.如图,下列条件:①∠DCA=∠CAF,②∠C=∠EDB,③∠BAC+∠C=180°,④∠GDE+∠B=180°.其中能判断AB//CD的是( )A. ①④ B. ②③④ C. ①③④ D. ①②③9.如图,在经过直线a外一点O的4条直线中,与直线a相交的直线至少有 ( ) A. 4条 B. 3条 C. 2条 D. 1条10.如图,下面哪个条件不能判断EF//DC的是( ) A. ∠1=∠2 B. ∠4=∠C C. ∠1+∠3=180° D. ∠3+∠C=180°二、填空题:11.如图,不添加辅助线,请写出一个能判定AD//BC的条件:________. 12.(教材P36复习题T8(1)变式)如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°.能判定AB//CD的有________.(填序号) 13.如图,过点F作EF//AB.因为AB//CD,所以EF__________CD(__________________________________). 14.如图,已知直线EF⊥MN垂足为F,且∠1=140°,则当∠2等于______时,AB//CD. 15.如图,点E是BA延长线上一点,下列条件中:①∠1=∠3;②∠5=∠D;③∠2=∠4;④∠B+∠BCD=180°,能判定AB//CD的有 .(填序号) 三、解答题:16.如图,已知∠COF+∠C=180°,∠C=∠B.试说明:AB//EF. 17.如图,已知AD⊥BC,EF⊥BC,∠B+∠1=90°,∠1=∠2,图中有哪些平行线?说明你的理由. 18.如图,点B在AC上,BD⊥BE,∠1+∠C=90°,则射线CF与BD平行吗?试用两种方法说明理由. 19.如图,点B在AC上,BD⊥BE,∠1+∠C=90°,试说明:BD//CF.思路一:利用同位角相等说明BD//CF.思路二:利用同旁内角互补说明BD//CF.20.如图,直线AE,CD相交于点O,如果∠A=110°,∠1=70°,试问AB//CD吗?为什么? 参考答案1.B 2.B 3.C 4.B 5.B 6.D 7.A 8.C 9.B 10.C 11.∠EAD=∠B(或∠DAC=∠C或∠DAB+∠B=180°) 12.③④ 13.//,平行于同一直线的两条直线平行 14.50° 15.②③④ 16.解:∵∠COF+∠C=180°,∴EF//CD,∵∠C=∠B,∴AB//CD,∴AB//EF. 17.解:平行线有AD // EF,DG // BA. 理由如下:∵AD⊥BC,EF⊥BC, ∴∠EFC=∠ADC=90°, ∴EF // AD. ∵∠B+∠1=90°,∠2+∠CDG=90°,∠1=∠2, ∴∠B=∠CDG. ∴DG // BA. 18.解:CF // BD. 理由如下:方法一: ∵BD⊥BE, ∴∠DBE=90°. ∴∠1+∠2=90°. 又∵∠1+∠C=90°, ∴∠2=∠C. ∴∠CF // BD. 方法二:∵BE⊥BD, ∴∠DBE=90°. ∵∠1+∠C=90°. ∴∠DBE+∠1+∠C=180°, 即∠DBC+∠C=180°. ∴CF // BD. 19.解:思路一:因为BD⊥BE, 所以∠DBE=90°. 所以∠1+∠2=180°−∠DBE=180°−90°=90°. 因为∠1+∠C=90°, 所以∠2=∠C. 所以BD // CF(同位角相等,两直线平行).思路二:因为BD⊥BE, 所以∠DBE=90°. 因为∠1+∠C=90°, 所以∠DBE+∠1+∠C=90°+90°=180°, 即∠DBC+∠C=180°. 所以BD // CF(同旁内角互补,两直线平行). 20.解:AB // CD. 理由如下:∵直线AE,CD相交于点O, ∴∠AOD=∠1=70°. 又∵∠A=110°, ∴∠A+∠AOD=180°. ∴AB // CD(同旁内角互补,两直线平行).
5.2平行线及其判定同步练习选择题:1.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出AB//DC的是( ) A. ①② B. ①③ C. ②③ D. ②④2.如图,下列推理不正确的是( ) A. 因为∠1=∠2,所以AE//BD B. 因为∠1=∠2,所以AB//ED C. 因为∠3=∠4,所以AB//CD D. 因为∠5=∠2+∠4,所以AE//BD3.(2023·贵阳期末)如图是小星探索两直线平行的条件时所用的学具,木条a,b,c在同一平面内,经测量∠1=65°,要使木条a//b,则∠2的度数应为 ( ) A. 25° B. 55° C. 65° D. 75°4.如图,过C点作直线AB的平行线,下列说法正确的是 ( ) A. 不能作 B. 只能作一条 C. 能作两条 D. 能作无数条5.如图,由∠B=∠DCE,可以得出的结论是 ( ) A. AD//BC B. AB//CD C. CA平分∠BCD D. AC平分∠BAD6.如图,直线a,b被直线c,d所截.下列条件能判定a//b的是( )A. ∠1=∠3 B. ∠2+∠4=180° C. ∠4=∠5 D. ∠1=∠27.下列图形中,由∠1+∠2=180°能推理得到AB//CD的是 ( )A. B. C. D. 8.如图,下列条件:①∠DCA=∠CAF,②∠C=∠EDB,③∠BAC+∠C=180°,④∠GDE+∠B=180°.其中能判断AB//CD的是( )A. ①④ B. ②③④ C. ①③④ D. ①②③9.如图,在经过直线a外一点O的4条直线中,与直线a相交的直线至少有 ( ) A. 4条 B. 3条 C. 2条 D. 1条10.如图,下面哪个条件不能判断EF//DC的是( ) A. ∠1=∠2 B. ∠4=∠C C. ∠1+∠3=180° D. ∠3+∠C=180°二、填空题:11.如图,不添加辅助线,请写出一个能判定AD//BC的条件:________. 12.(教材P36复习题T8(1)变式)如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°.能判定AB//CD的有________.(填序号) 13.如图,过点F作EF//AB.因为AB//CD,所以EF__________CD(__________________________________). 14.如图,已知直线EF⊥MN垂足为F,且∠1=140°,则当∠2等于______时,AB//CD. 15.如图,点E是BA延长线上一点,下列条件中:①∠1=∠3;②∠5=∠D;③∠2=∠4;④∠B+∠BCD=180°,能判定AB//CD的有 .(填序号) 三、解答题:16.如图,已知∠COF+∠C=180°,∠C=∠B.试说明:AB//EF. 17.如图,已知AD⊥BC,EF⊥BC,∠B+∠1=90°,∠1=∠2,图中有哪些平行线?说明你的理由. 18.如图,点B在AC上,BD⊥BE,∠1+∠C=90°,则射线CF与BD平行吗?试用两种方法说明理由. 19.如图,点B在AC上,BD⊥BE,∠1+∠C=90°,试说明:BD//CF.思路一:利用同位角相等说明BD//CF.思路二:利用同旁内角互补说明BD//CF.20.如图,直线AE,CD相交于点O,如果∠A=110°,∠1=70°,试问AB//CD吗?为什么? 参考答案1.B 2.B 3.C 4.B 5.B 6.D 7.A 8.C 9.B 10.C 11.∠EAD=∠B(或∠DAC=∠C或∠DAB+∠B=180°) 12.③④ 13.//,平行于同一直线的两条直线平行 14.50° 15.②③④ 16.解:∵∠COF+∠C=180°,∴EF//CD,∵∠C=∠B,∴AB//CD,∴AB//EF. 17.解:平行线有AD // EF,DG // BA. 理由如下:∵AD⊥BC,EF⊥BC, ∴∠EFC=∠ADC=90°, ∴EF // AD. ∵∠B+∠1=90°,∠2+∠CDG=90°,∠1=∠2, ∴∠B=∠CDG. ∴DG // BA. 18.解:CF // BD. 理由如下:方法一: ∵BD⊥BE, ∴∠DBE=90°. ∴∠1+∠2=90°. 又∵∠1+∠C=90°, ∴∠2=∠C. ∴∠CF // BD. 方法二:∵BE⊥BD, ∴∠DBE=90°. ∵∠1+∠C=90°. ∴∠DBE+∠1+∠C=180°, 即∠DBC+∠C=180°. ∴CF // BD. 19.解:思路一:因为BD⊥BE, 所以∠DBE=90°. 所以∠1+∠2=180°−∠DBE=180°−90°=90°. 因为∠1+∠C=90°, 所以∠2=∠C. 所以BD // CF(同位角相等,两直线平行).思路二:因为BD⊥BE, 所以∠DBE=90°. 因为∠1+∠C=90°, 所以∠DBE+∠1+∠C=90°+90°=180°, 即∠DBC+∠C=180°. 所以BD // CF(同旁内角互补,两直线平行). 20.解:AB // CD. 理由如下:∵直线AE,CD相交于点O, ∴∠AOD=∠1=70°. 又∵∠A=110°, ∴∠A+∠AOD=180°. ∴AB // CD(同旁内角互补,两直线平行).
相关资料
更多









