人教版八年级上册12.1 全等三角形单元测试精练

这是一份人教版八年级上册12.1 全等三角形单元测试精练，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题(共10 小题，每小题3分，共30 分)
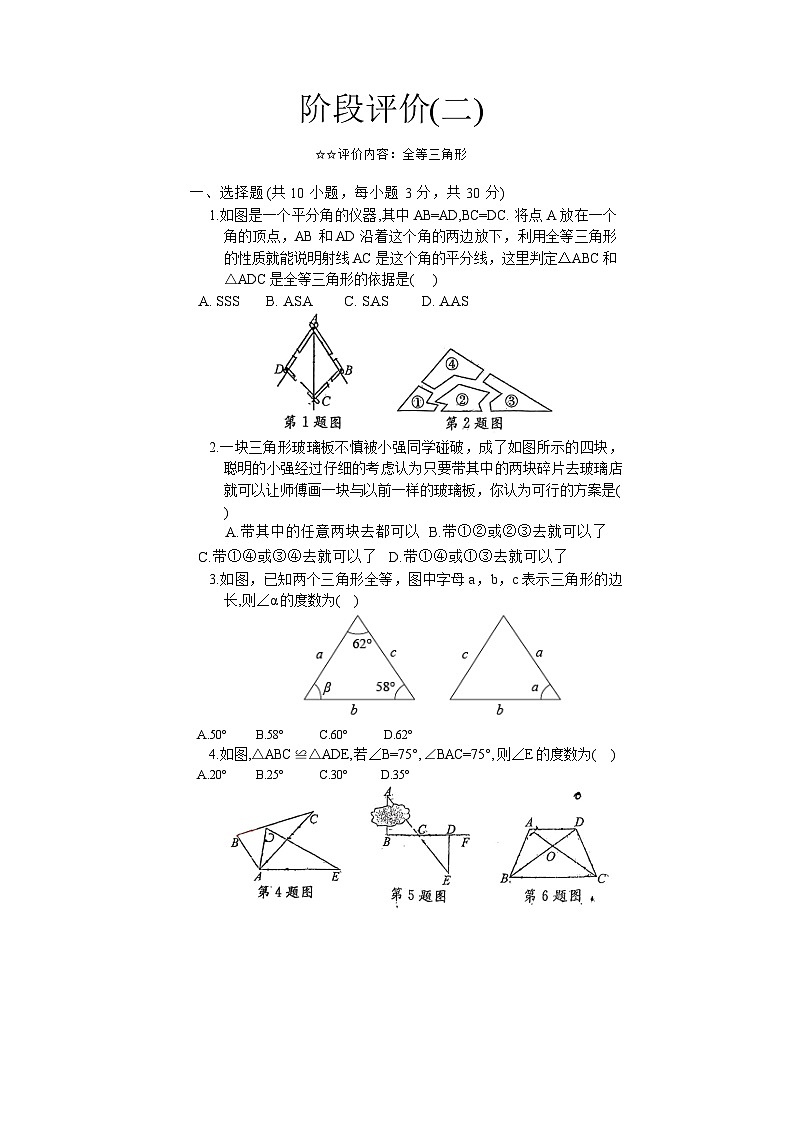
1.如图是一个平分角的仪器,其中AB=AD,BC=DC.将点 A放在一个角的顶点，AB 和AD 沿着这个角的两边放下，利用全等三角形的性质就能说明射线 AC是这个角的平分线，这里判定△ABC和△ADC是全等三角形的依据是( )
A. SSS B. ASA C. SAS D. AAS
2.一块三角形玻璃板不慎被小强同学碰破，成了如图所示的四块，聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃板，你认为可行的方案是( )
A.带其中的任意两块去都可以 B.带①②或②③去就可以了
C.带①④或③④去就可以了 D.带①④或①③去就可以了
3.如图，已知两个三角形全等，图中字母a，b，c表示三角形的边长,则∠α的度数为( )

A.50° B.58° C.60° D.62°
4.如图,△ABC≌△ADE,若∠B=75°,∠BAC=75°,则∠E的度数为( )
A.20° B.25° C.30° D.35°
5.如图，为了测量池塘两岸相对的两点 A，B之间的距离，小颖在池塘外取AB的垂线 BF 上两点C, D,使 BC=CD,再画出 BF的垂线DE，使点E 与A，C在同一条直线上，这时，可得△ABC≌△EDC,因此,测得 DE 的长就是 AB 的长.这里判定△ABC≌△EDC的依据是( ).
A. ASA B. SAS C. AAS D. SSS
6.如图,∠ABC=∠DCB=70°,∠ABD=40°, AB=DC,则∠BAC=( )
A.70° B.80° C.100° D.90°
7.(临沂)如图,D 是AB 上一点,DF 交 AC 于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C,1.5 D.2
8.如图,△ABC中,∠A=90°,∠B=30°,CD平分∠ACB交AB于点D,DE∥AC,交 BC于点E,若AC=6,则DE长为(
A.3 B.4 C.5 D.6
9.(青岛)如图,BD是△ABC 的角平分线,AE⊥BD,垂足为 F.若∠ABC=35°,∠C=50°,则∠CDE 的度数为( ).
A.35° B.40° C.45° D.50°
10.(滨州)如图,在△OAB 和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;② AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( )
A.4 B.3 C.2 D.1
二、填空题(共6 小题，每小题3 分，共18 分)
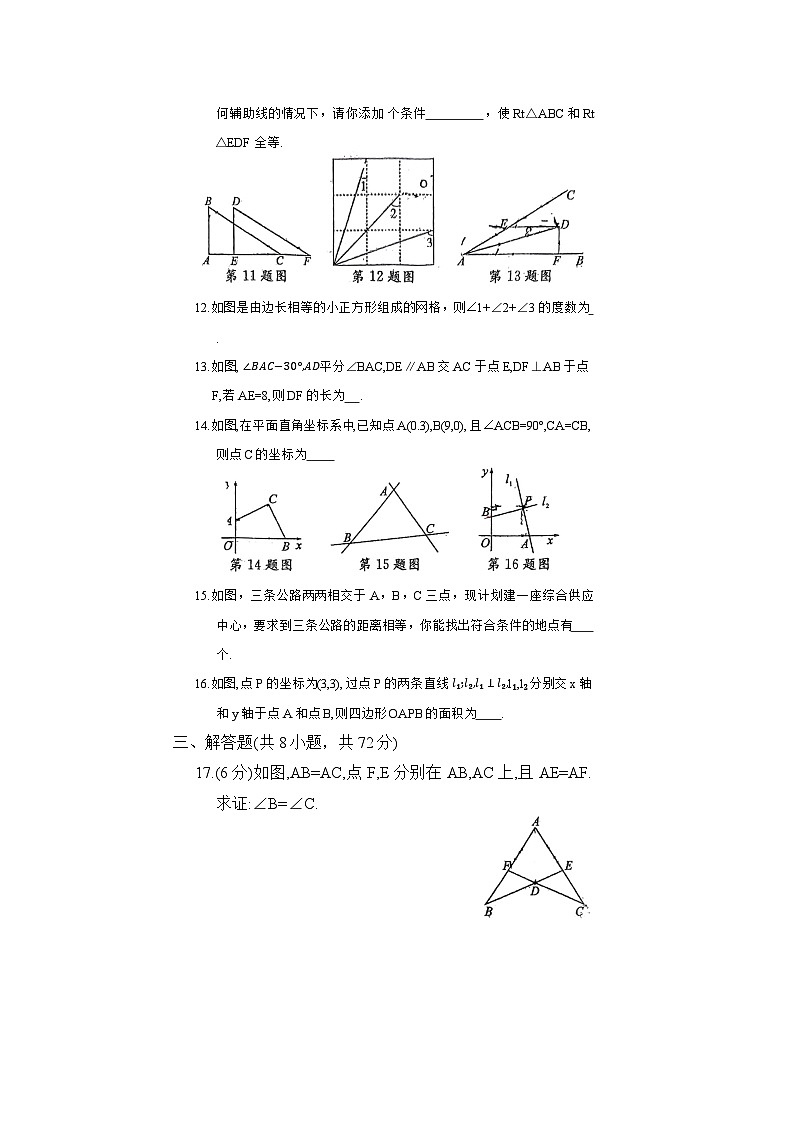
11.如图,在 Rt△ABC和 Rt△EDF 中,BC∥DF,在不添加任何辅助线的情况下，请你添加 个条件 ，使Rt△ABC和Rt△EDF 全等.
12.如图是由边长相等的小正方形组成的网格，则∠1+∠2+∠3的度数为 .
13.如图, ∠BAC−30°,AD平分∠BAC,DE∥AB交AC 于点E,DF⊥AB于点F,若AE=8,则DF的长为 .
14.如图,在平面直角坐标系中,已知点 A(0.3),B(9,0),且∠ACB=90°,CA=CB,则点 C的坐标为
15.如图，三条公路两两相交于 A，B，C三点，现计划建一座综合供应中心，要求到三条公路的距离相等，你能找出符合条件的地点有 个.
16.如图,点 P 的坐标为(3,3),过点 P 的两条直线 l₁;l₂,l₁⊥l₂,l₁,l₂分别交x轴和y 轴于点 A 和点 B,则四边形OAPB的面积为 .
三、解答题(共8小题，共72分)
17.(6 分)如图,AB=AC,点 F,E 分别在AB,AC上,且AE=AF.求证:∠B=∠C.
18.(7分) 如图所示,两根旗杆AC,BD间相距12 m,某人从点B沿BA走向A，一段时间后他到达点 M，此时他仰望旗杆的顶点 C 和D，两次视线的夹角为 90°,且 CM=DM。已知旗杆 AC的高为3m，该人的运动速度为 1m/s,，求这个人从点 B 到达点 M 用了多长时间?
19.(10分)要测量不能直接到达的池塘两岸A，B两点的距离，有的同学采用了这样的方法：
(1)如图，要测量水池的宽AB，过 A 作线段. AC⊥AB,再由点C观测，在 BA的延长线上找一点 B₁,使 ∠ACB₁= ∠ACB,，这时只要量出. AB₁的长度，就知道 AB 的长了.这种做法对吗? 请说明理由；
(2)你一定还有更好的测量 AB的方法，请说出一种.(要求画出图形，简述测量方法，并说明你的做法是正确的)
A
B
20.(8分)(徐州)如图, AC⟂BCDC⟂EC,AC=BC,DC=EC,AE 与BD 交于点F.
(1)求证: AE=BD;
(2)求 ∠AFD的度数.
21.(10 分)如图,在 △ABC中, AB=AC,点D,E,F 分别在边BC,AC,AB上,且. BD=CE,DC=BF,且 ∠EDF=60°.
(1)求证: △BDF≅△CED;
(2)判断 △ABC的形状，并说明理由.
22.(9 分)如图,在 △ABC中, ∠ABC=∠BAC=45°,点 P 在AB 上. AD⟂CP,BE⟂CP,，垂足分别为点 D，E，已知. DC=2,求 BE 的长.
23.(10 分)如图,已知 △ABC中, AB=AC=10cm,BC=3cm,点 D 为AB 的中点.如果点 P 在线段BC 上以 3cm/s的速度由点 B 向点C 运动，同时，点Q在线段CA 上由点C 向点A 运动.
(1)若点Q与点P 的运动速度相等,经过1 s后,△BPD与 △CQP是否全等? 请说明理由；
(2)若点 Q 与点 P 的运动速度不相等，当点 Q 的运动速度为多少时，能使 △BPD与 △CQP全等?
24.(12 分)如图,在 △ABC中,D 是 BC 的中点,过点 D 的直线GF 交AC 于点F,交 AC 的平行线 BG 于点G, DE⊥DF交AB 于点E,连接 EG,EF.
(1)求证: BG=CF;
(2)请你判断. BE+CF与EF 的大小关系，并说明理由.