2023九年级数学上册第4章锐角三角函数4.2正切上课课件新版湘教版

这是一份2023九年级数学上册第4章锐角三角函数4.2正切上课课件新版湘教版，共23页。
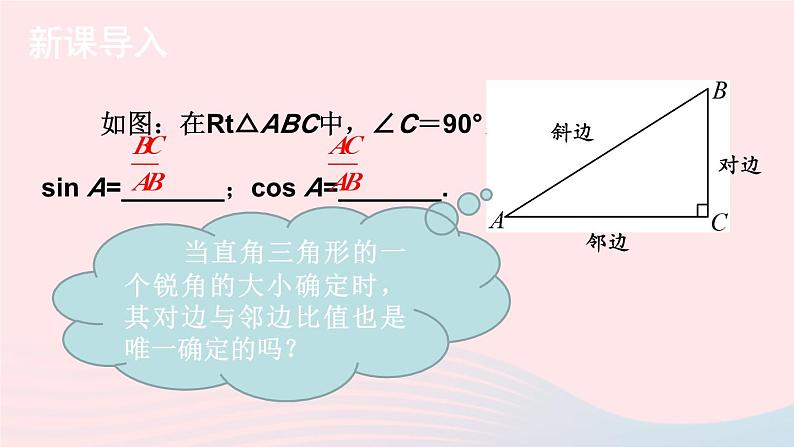
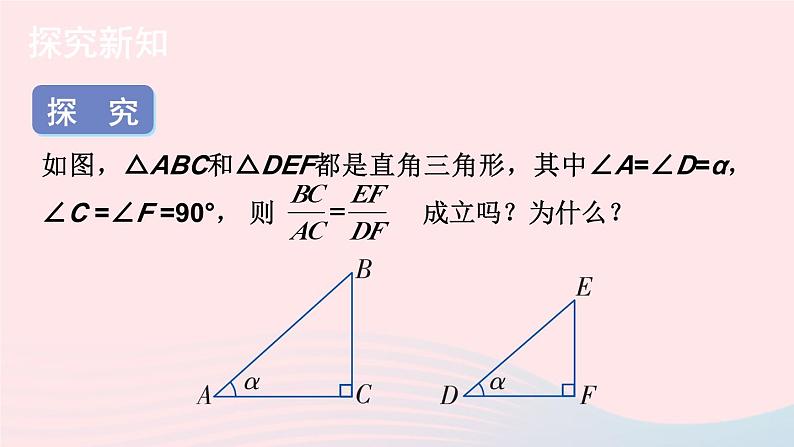
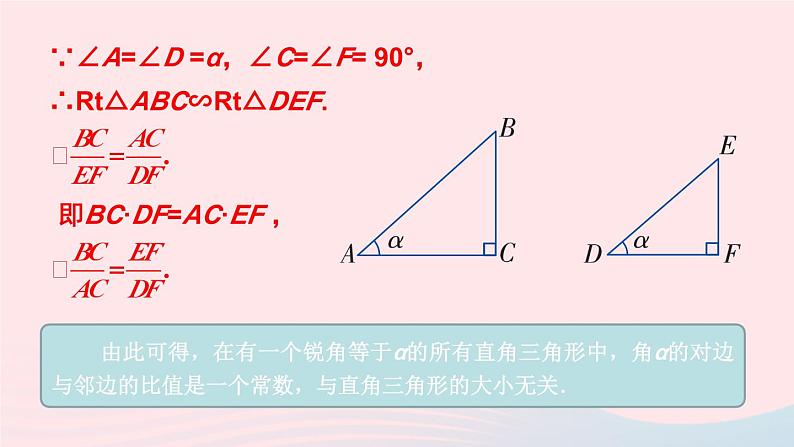
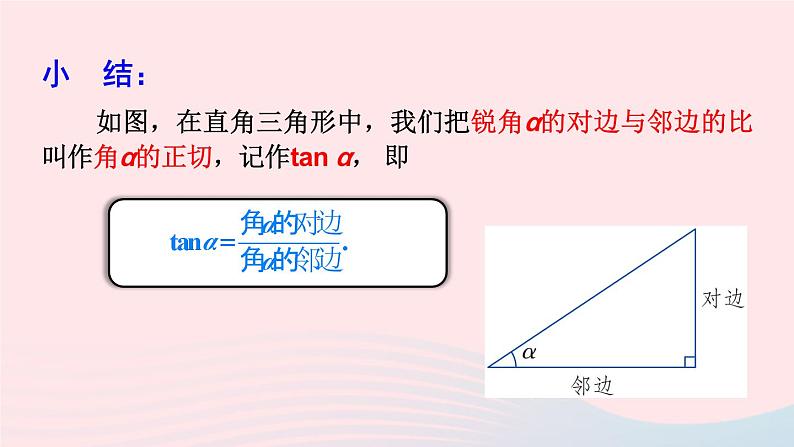
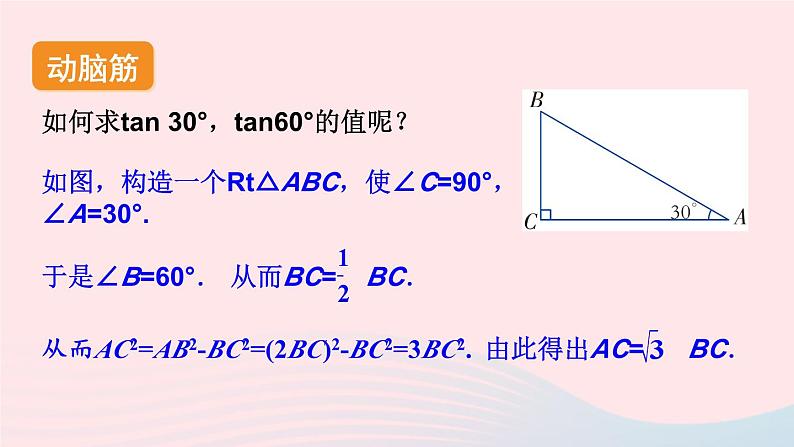
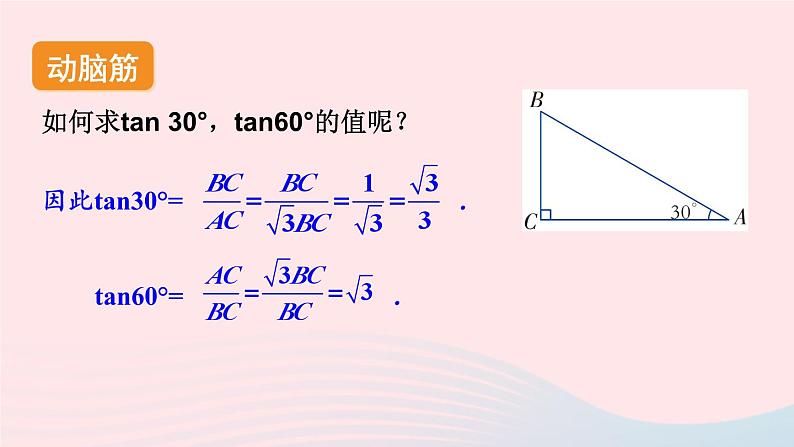
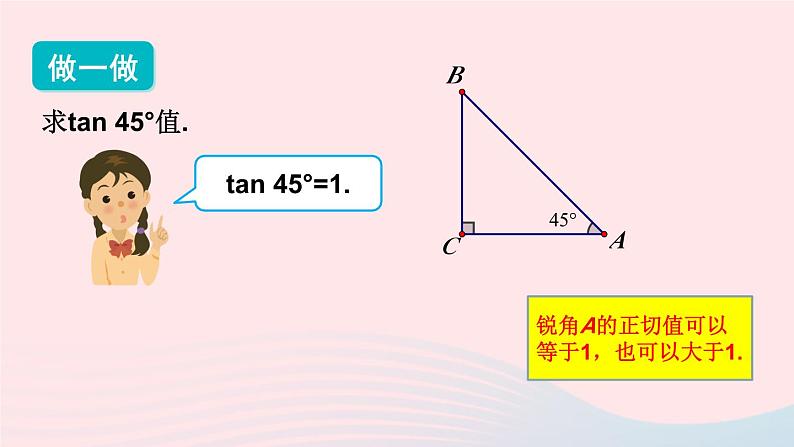
湘教·九年级上册4.2 正切新课导入 如图：在Rt△ABC中，∠C＝90°，sin A=_______；cos A=_______. 当直角三角形的一个锐角的大小确定时，其对边与邻边比值也是唯一确定的吗？斜边邻边对边探 究探究新知如图，△ABC和△DEF都是直角三角形，其中∠A=∠D=α，∠C =∠F =90°， 则 成立吗？为什么？∵∠A=∠D =α，∠C=∠F= 90°，∴Rt△ABC∽Rt△DEF.即BC·DF=AC·EF ， 由此可得，在有一个锐角等于α的所有直角三角形中，角α的对边与邻边的比值是一个常数，与直角三角形的大小无关．小 结： 如图，在直角三角形中，我们把锐角α的对边与邻边的比叫作角α的正切，记作tan α， 即动脑筋如何求tan 30°，tan60°的值呢？如图，构造一个Rt△ABC，使∠C=90°，∠A=30°.于是∠B=60°．从而AC2=AB2-BC2=(2BC)2-BC2=3BC2.动脑筋如何求tan 30°，tan60°的值呢？因此tan30°= .tan60°= .做一做求tan 45°值.tan 45°=1.锐角A的正切值可以等于1，也可以大于1. 现在我们把30°，45°，60°的正弦、余弦、正切值列表归纳如下： 观 察：1.你能得出互为余角的两个锐角A、B正切值的关系吗？2.你能得出一个锐角A的正弦值、余弦值和正切值的关系吗？小 结：在Rt△ABC中，若∠A+∠B=90°，则tan A·tan B=1. 对于一般锐角(30°，45°，60°除外)的正切值，我们也可用计算器来求. 如果已知正切值，我们也可以利用计算器求出它的对应锐角. 例如，已知tanα=0.8391，依次按键显示结果为40.000…，表示角α约等于40°.做一做利用计算器计算：（1）tan21°15′≈ ______________（精确到0.0001）；（2）tan89°27′≈ ______________（精确到0.0001）；（3）若tan α=1.286 8，则 α ≈ ___________（精确到0.1°）；（4）若tan α=108.572 9，则 α ≈ _________（精确到0.1°）.0.3889104.170952.2°89.5°例：计算：tan45°+tan230°tan260°.解：tan45°+tan230°tan260°.练习1.在Rt△ABC中，∠C=90°，AC=7， BC=5，求 tan A，tan B 的值．解：2.用计算器求下列锐角的正切值（精确到0.0001）：（1） 35°； （2） 68°12′； （3） 9°42′.解：（1）tan35°≈ 0.7002；（2）tan68°12′≈ 2.5001；（3）tan9°42′≈ 0.1709.3.已知下列正切值，用计算器求对应的锐角（精确到0.1°）.（1）tan α=0.1087； （2）tan α=89.7081.解：（1）α ≈ 6.2°；（2）α ≈ 89.4°；4.计算：（1）1+tan260°； （2） tan30°cos30°.解：1+tan260°解：tan30°cos30°5.如图，在Rt△ABC中，∠C=90°，∠A=35°，AC=6，求BC，AB的长.（精确到0.001）由计算器求得tan35°≈0.7002，∴BC=AC·tan A≈6×0.7002≈4.201.由计算器求得sin35°≈0.5736，6.如图，工件上有一V型槽，测得它的上口宽20 mm，深19.2 mm.求V型角（∠ACB）的大小（结果精确到度）. ∴∠ACD≈27.51°.∴∠ACB=2∠ACD≈2×27.51≈55°.∴V型角的大小约为55°.课堂小结 如图，在直角三角形中，我们把锐角α的对边与邻边的比叫作角α的正切，记作tan α， 即