浙江省杭州市西湖区2023-2024学年九年级上学期期末数学试题()

这是一份浙江省杭州市西湖区2023-2024学年九年级上学期期末数学试题()，共6页。试卷主要包含了四边形内接于，则满足条件等内容，欢迎下载使用。

考生须知：
1．本试卷分试题卷和答题卷两部分，满分120分，考试时间120分钟．
2．答题前，必须在答题卷上填写姓名等信息．
3．不允许使用计算器进行计算，凡题目中没有要求取近似值的，结果中应保留根号或．
一、选择题：本大题有10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．若均不为0，则的值是（ ）
A．6 B．3 C．2 D．1
2．下列二次函数中，对称轴是直线的是（ ）
A． B． C． D．
3．不透明的袋子中只有2个黑球和1个白球，这些球除颜色外无其他差别，随机从袋子中一次摸出2个球，下列事件是不可能事件的是（ ）
A．2个球都是黑球 B．2个球都是白球
C．2个球中有黑球 D．2个球中有白球
4．四边形内接于，则满足条件（ ）
A． B． C． D．
5．如图，与是位似图形，点为位似中心，已知的周长为1，则的周长为（ ）
A．1 B．2 C．4 D．8
6．已知二次函数，则下列表述正确的是（ ）
A．若，抛物线的开口向下 B．当时，随的增大而增大
C．图象与轴一定有两个交点 D．图象与轴的交点坐标为
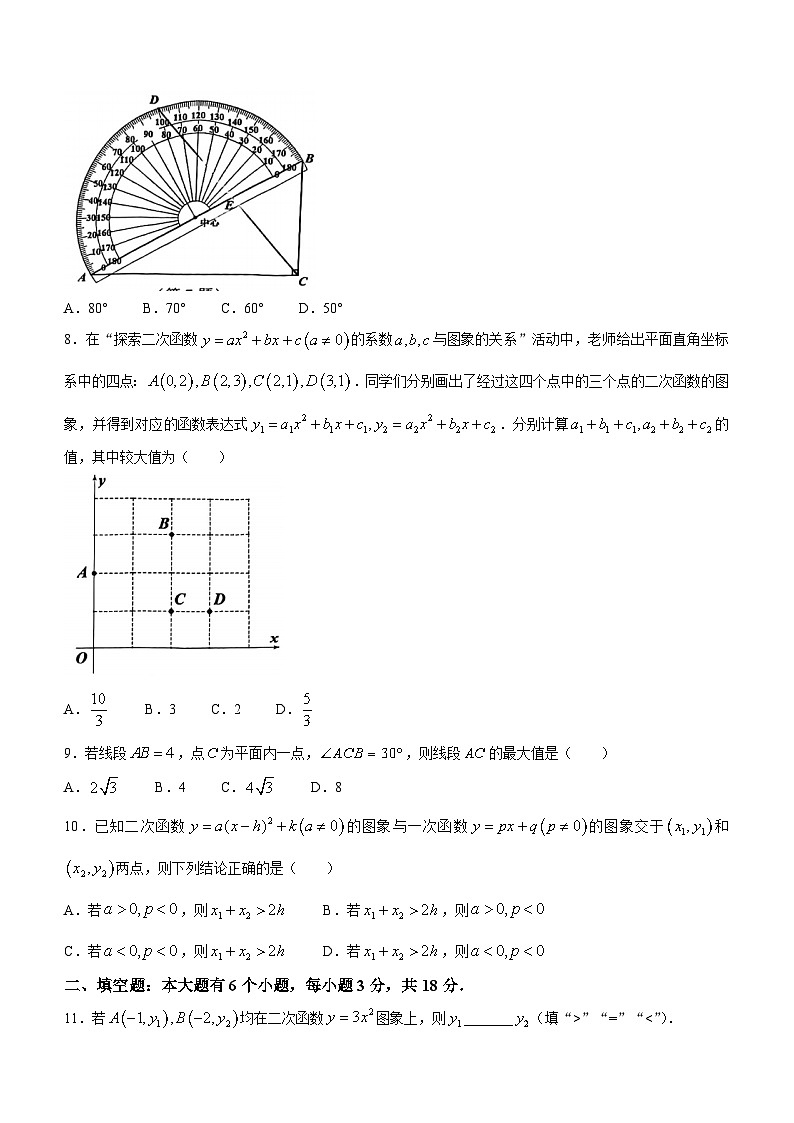
7．如图，将一个含角的直角三角板的斜边和量角器的直径所在的边重合放置，其中点所在位置在量角器外侧的读数为，连接交于点，则（ ）
A．80° B．70° C．60° D．50°
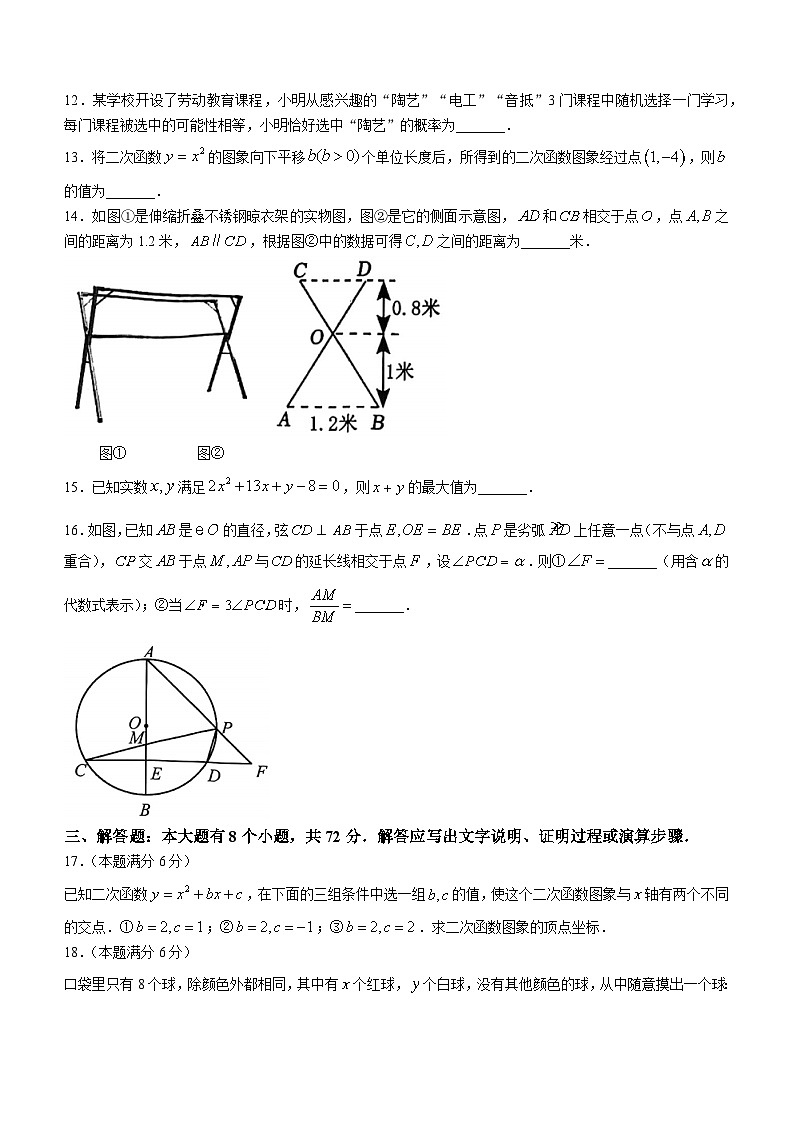
8．在“探索二次函数的系数与图象的关系”活动中，老师给出平面直角坐标系中的四点：．同学们分别画出了经过这四个点中的三个点的二次函数的图象，并得到对应的函数表达式．分别计算的值，其中较大值为（ ）
A． B．3 C．2 D．
9．若线段，点为平面内一点，，则线段的最大值是（ ）
A． B．4 C． D．8
10．已知二次函数的图象与一次函数的图象交于和两点，则下列结论正确的是（ ）
A．若，则 B．若，则
C．若，则 D．若，则
二、填空题：本大题有6个小题，每小题3分，共18分．
11．若均在二次函数图象上，则_______（填“>”“=”“<”）．
12．某学校开设了劳动教育课程，小明从感兴趣的“陶艺”“电工”“音抵”3门课程中随机选择一门学习，每门课程被选中的可能性相等，小明恰好选中“陶艺”的概率为_______．
13．将二次函数的图象向下平移个单位长度后，所得到的二次函数图象经过点，则的值为_______．
14．如图①是伸缩折叠不锈钢晾衣架的实物图，图②是它的侧面示意图，和相交于点，点之间的距离为1.2米，，根据图②中的数据可得之间的距离为_______米．
图① 图②
15．已知实数满足，则的最大值为_______．
16．如图，已知是的直径，弦于点．点是劣弧上任意一点（不与点重合），交于点与的延长线相交于点，设．则①_______（用含的代数式表示）；②当时，_______．
三、解答题：本大题有8个小题，共72分．解答应写出文字说明、证明过程或演算步骤．
17．（本题满分6分）
已知二次函数，在下面的三组条件中选一组的值，使这个二次函数图象与轴有两个不同的交点．①；②；③．求二次函数图象的顶点坐标．
18．（本题满分6分）
口袋里只有8个球，除颜色外都相同，其中有个红球，个白球，没有其他颜色的球，从中随意摸出一个球：
（1）如果摸到红球与摸到白球的可能性相等，分别求和的值．
（2）在（1）的条件下，现从布袋中取走若干个白球，并放入相同数目的红球，搅拌均匀后，再从口袋中摸出一个球是红球的概率是，求取走多少个白球．
19．（本题满分8分）
设二次函数是常数，，部分对应值如表：
（1）请直接写出该函数图象的开口方向．
（2）根据你的解题经验，直接写出的解．
（3）当时，求函数的值．
20．（本题满分8分）
如图，在中，是的角平分线，点是边上一点，且满足．
（1）证明：．
（2）若，求的长．
21．（本题满分10分）
在平面直角坐标系中，点都在二次函数的图象上．
（1）若，求的值．
（2）若，求的取值范围．
22．（本题满分10分）
如图，四边形内接于为的直径，且．
（1）试判断的形状，并给出证明．
（2）若．
①求线段的长．
②求的值．
23．（本题满分12分）
定义：由两条与x轴有相同的交点，并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”．
【概念理解】
抛物线与抛物线是否围成“月牙线”？说明理由．
【尝试应用】
抛物线与抛物线组成一个如图所示的“月牙线”，与轴有相同的交点，（点在点的左侧），与轴的交点分别为．
①求的值．
②已知点和点在“月牙线”上，，且的值始终不大于2，求线段长的取值范围．
24．（本题满分12分）
如图，是正方形边上一个动点（不与重合），是延长线上一点，且，连接．
（1）求证：为等腰直角三角形．
（2）过点作的垂线，与直线分别交于两点，记交于点．
①当，求线段的长．
②设的面积记作的面积记作，用含的代数式表示． …
0
1
2
…
…
5
0
…