浙江省嘉兴市2023-2024学年八年级上学期期末数学试题(含答案)

这是一份浙江省嘉兴市2023-2024学年八年级上学期期末数学试题(含答案)，共9页。试卷主要包含了1）等内容，欢迎下载使用。
（2024.1）
【考生须知】1．本卷为试题卷，请将答案做在答题卷上；
2．本次检测不使用计算器．
一、选择题（每小题有4个选项，其中有且只有一个正确．请把正确选项的代码填入答题卷的相应空格，每小题3分，共30分）
1．下列图形为轴对称图形的是（ ）
A． B．
C． D．
2．下列各点中位于第二象限的是（ ）
A． B． C． D．
3．如图是某校园内对汽车的限速标志，表示该校园内汽车行驶的速度x（千米/小时）应满足的不等关系为（ ）
A． B． C． D．
4．已知一次函数的图象经过点,则该函数的图象不经过（ ）
A．第一象限 B．第二象限且 C．第三象限 D．第四象限
5．下列长度的线段能组成三角形的是（ ）
A． B． C． D．
6．不等式组的解为（ ）
A． B． C． D．
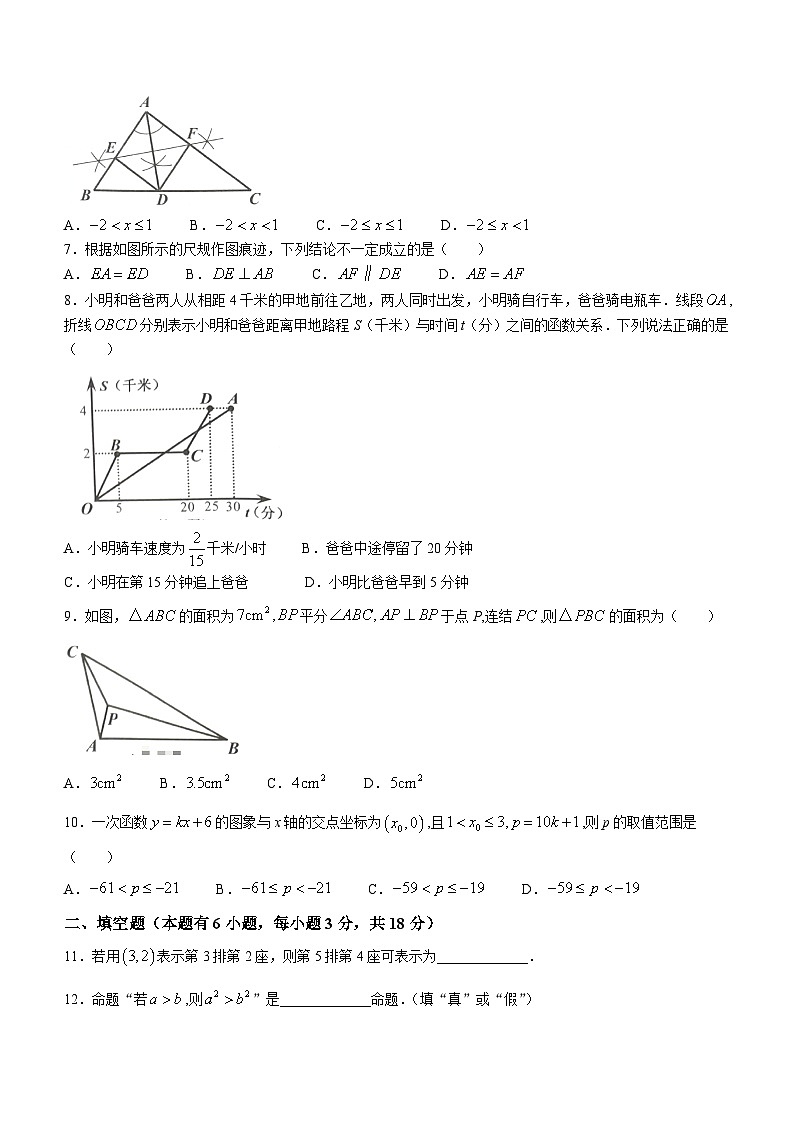
7．根据如图所示的尺规作图痕迹，下列结论不一定成立的是（ ）
A． B． C． D．
8．小明和爸爸两人从相距4千米的甲地前往乙地，两人同时出发，小明骑自行车，爸爸骑电瓶车．线段,折线分别表示小明和爸爸距离甲地路程S（千米）与时间t（分）之间的函数关系．下列说法正确的是（ ）
A．小明骑车速度为千米/小时 B．爸爸中途停留了20分钟
C．小明在第15分钟追上爸爸 D．小明比爸爸早到5分钟
9．如图，的面积为平分于点P,连结,则的面积为（ ）
A． B． C． D．
10．一次函数的图象与x轴的交点坐标为,且,则p的取值范围是（ ）
A． B． C． D．
二、填空题（本题有6小题，每小题3分，共18分）
11．若用表示第3排第2座，则第5排第4座可表示为_____________．
12．命题“若,则”是_____________命题．（填“真”或“假”）
13．如图，将一副三角尺叠放在一起，其中点B,E,C三点共线，则的度数为_____________．
14．一艘轮船8：00从A港出发向西航行，10：00折向北航行，平均航速均为20千米/时，则11：30时该轮船离A港的距离为_____________．
15．如图，函数与的图象相交于点,则关于x的不等式的解为_____________．
16．如图，中，，点D是上一动点，将沿折叠得到,当与重叠部分是直角三角形时，的度数为_____________．
三、解答题（本题有8小题，第17~22题每题6分，第23、24题每题8分，共52分）
17．在解不等式时，小马同学给出了如下解法：
解：去括号，得．
移项，得．
合并同类项，得．
两边都除以，得．
判断小马同学的解法是否有错误？若有错误，请写出正确的解答过程．
18．如图，是的斜边上的中线，．
（1）求的度数．
（2）若,求的周长．
19．已知一次函数的图象经过点．
（1）求此一次函数的表达式．
（2）判断点是否在该函数图象上，并说明理由．
20．把点向左平移3个单位得到点．
（1）当时，求点的坐标．
（2）若点与点A关于y轴对称，求a的值．
21．如图，．
（1）求证：．
（2）判断的形状，并说明理由．
22．如图，在直角坐标系中，已知点,直线l是第二、四象限的角平分线．
（1）操作：连结线段,作出线段关于直线l的轴对称图形．
（2）发现：请写出坐标平面内任一点关于直线l的对称点的坐标．
（3）应用：请在直线l上找一点Q,使得最小，并写出点Q的坐标．
23．根据表中素材，探索完成以下任务：
24．如图，在直角坐标系中，点,点B为x轴正半轴上一个动点，以为边作,使，且点C在第一象限内．
图1 图2 图3
（1）如图1，若,求点C的坐标．
（2）如图2，过点B向x轴上方作,且,在点B的运动过程中，探究点C,D之间的距离是否为定值．若为定值，求出该定值，若不是，请说明理由．
（3）如图3，过点B向x轴下方作,且,连结交x轴于点E,当的面积是的面积的2倍时，求的长．
嘉兴市八年级（上）学科期末检测
数学 参考答案
一、选择题（每小题有4个选项，其中有且只有一个正确．请把正确选项的代码填入答题卷的相应空格，每小题3分，共30分）
二、填空题（本题有6小题，每小题3分，共18分）
11．；12．假；13．；14．50千米；15．；16．或或．
三、解答题（本题有8小题，第17~22题每题6分，第23、24题每题8分，共52分）
17．解：有错误． 2分
正确解答如下：
去括号，得． 1分
移项，得． 1分
合并同类项，得． 1分
解得． 1分
18．（1）解：，，
． 3分
（2）解：是的斜边边上的中线，且,
, 1分
，
是等边三角形， 1分
的周长为15． 1分
19．解：（1）把点代入得：, 1分
解得：,故所求一次函数表达式为． 2分
（2）当时，, 2分
故点在该函数图象上． 1分
20．（1）． 3分
（2）解：由题意得， 1分
∵点与点A关于y轴对称，
1分
即． 1分
21．（1）证明：在和中，
,
, 2分
． 1分
（2）是等腰三角形，理由如下：
,, 2分
是等腰三角形． 1分
22．（1） 2分
（2） 2分
（3）． 2分
23．问题1： 2分
化简，得 1分
当时，则 2分
问题2：由题意得，设新的总运费为W,则 1分
,
随着x的增大而减小，∴当时，则． 2分
24．解：（1）过点C作轴于点，
, 1分
在和中，,
1分
．,
∴点C的坐标为． 1分
（2）点C,D之间的距离是为定值，理由如下：
连结，
, 1分
在和中，,
． 1分
（3）过点C作轴于点F,由（1）可知，,
．
在和中，
，
, 1分
由题可知,
．
, 1分
． 1分
其他解法酌情给分．
建设“美丽乡村”，落实“乡村振兴”
问题情境
素材1
己知甲、乙两仓库分别有水泥40吨和60吨．
素材2
现在A村需要水泥48吨，B村需要水泥52吨．
素材3
从甲仓库往A,B两村运送水泥的费用分别为20元/吨和25元/吨；
从乙仓库往A,B两村运送水泥的费用分别为15元/吨和24元/吨．
问题解决
分析
设从甲仓库运往A村水泥x吨，补全以下表格．
运量（吨）
运费（元）
甲仓库
乙仓库
甲仓库
乙仓库
A村
x
B村
①______
②________
问题1
设总运费为y元，请写出y与x的函数关系式并求出最少总运费．
问题2
为了更好地支援乡村建设，甲仓库运往A村的运费每吨减少元，这时甲仓库运往A村的水泥多少吨时总运费最少？最少费用为多少元？（用含a的代数式表示）
题号
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
A
B
A
B
C
B
C