

- 八年级数学下册尖子生培优必刷题 专题18.8平行四边形的性质与判定大题专练(重难点培优30题)(原卷版+解析) 试卷 0 次下载
- 八年级数学下册尖子生培优必刷题 专题18.3菱形的判定专项提升训练(重难点培优)(原卷版+解析) 试卷 0 次下载
- 八年级数学下册尖子生培优必刷题 专题18.6矩形的判定专项提升训练(重难点培优)(原卷版+解析) 试卷 0 次下载
- 八年级数学下册尖子生培优必刷题 专题18.7正方形专项提升训练(重难点培优)(原卷版+解析) 试卷 0 次下载
- 八年级数学下册尖子生培优必刷题 专题18.10菱形的性质与判定大题提升专练(重难点培优30题)(原卷版+解析) 试卷 0 次下载
人教版八年级下册18.2.1 矩形课时训练
展开班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷满分120分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
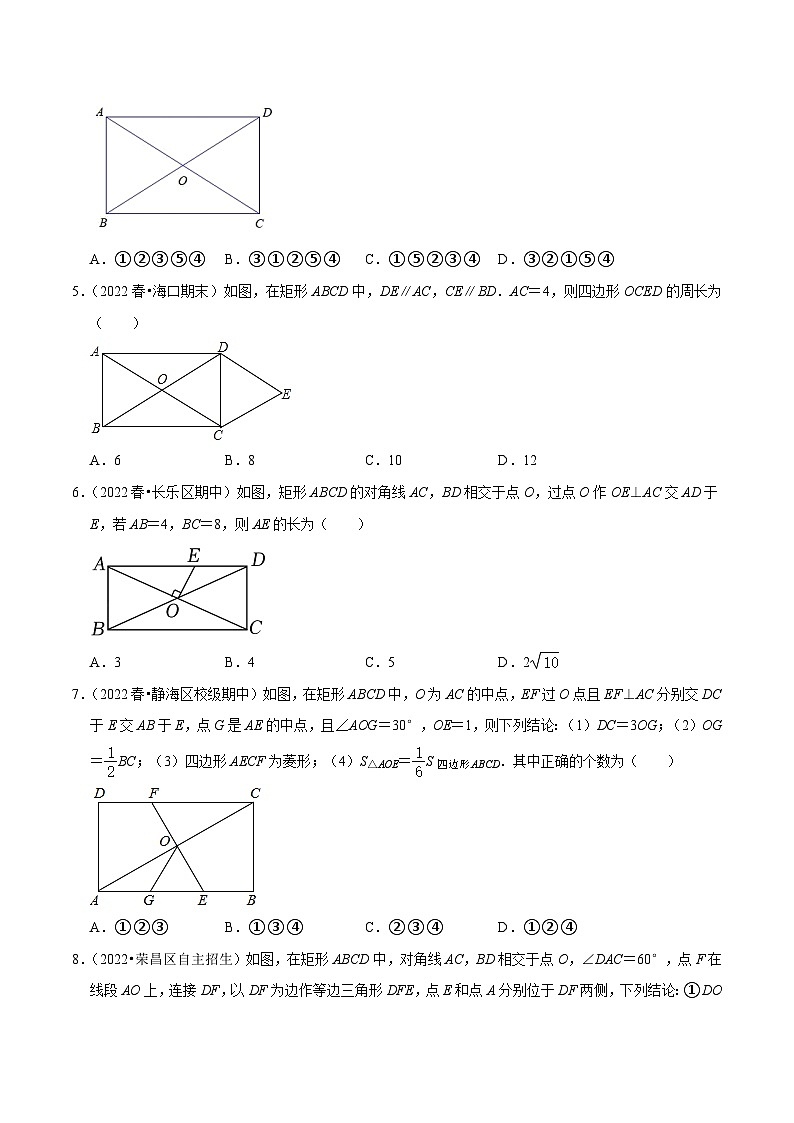
1.(2022春•阜平县期末)如图,AC,BD是矩形ABCD的对角线,∠AOB=40°,则∠ACD的度数为( )
A.50°B.55°C.65°D.70°
2.(2022春•喀什地区期末)如图,在矩形ABCD中,∠BOC=120°,AC=2,则AB的长为( )
A.1B.2C.D.
3.(2022春•覃塘区期末)在矩形ABCD中,若相邻的两边长分别是4和,则对角线所夹的锐角度数是( )
A.30°B.40°C.45°D.60°
4.(2022春•平泉市期末)求证:矩形的两条对角线相等.
已知:如图,四边形ABCD为矩形.求证:AC=BD.
以下是排乱的证明过程:
①∵BC=CB
②∴AB=CD,∠ABC=∠DCB
③∵四边形ABCD是矩形
④∴AC=DB
⑤∴△ABC≌△DCB
证明步骤正确的顺序是( )
A.①②③⑤④B.③①②⑤④C.①⑤②③④D.③②①⑤④
5.(2022春•海口期末)如图,在矩形ABCD中,DE∥AC,CE∥BD.AC=4,则四边形OCED的周长为( )
A.6B.8C.10D.12
6.(2022春•长乐区期中)如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AD于E,若AB=4,BC=8,则AE的长为( )
A.3B.4C.5D.2
7.(2022春•静海区校级期中)如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC于E交AB于E,点G是AE的中点,且∠AOG=30°,OE=1,则下列结论:(1)DC=3OG;(2)OG=BC;(3)四边形AECF为菱形;(4)S△AOE=S四边形ABCD.其中正确的个数为( )
A.①②③B.①③④C.②③④D.①②④
8.(2022•荣昌区自主招生)如图,在矩形ABCD中,对角线AC,BD相交于点O,∠DAC=60°,点F在线段AO上,连接DF,以DF为边作等边三角形DFE,点E和点A分别位于DF两侧,下列结论:①DO=DA;②DF=EC;③∠ADF=∠ECF;④∠BDE=∠EFC中正确结论的序号为( )
A.①④B.①②③C.②③④D.①②③④
9.(2022秋•章丘区期中)如图,在矩形ABCD中,AB=24,BC=12,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形.则AE的长是( )
A.15B.20C.D.
10.(2022秋•姜堰区期中)如图,在矩形ABCD中,AB=3cm,BC=cm,点P从A点出发沿AB以cm/s的速度向点B运动,当PA=PC时,点P运动的时间为( )
A.sB.2sC.10sD.10s或2s
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2022春•费县期末)如图所示.在矩形ABCD中,AB=2.BD=4,则∠AOD= 度.
12.(2022春•仙居县期末)如图,矩形ABCD中,AC与BD交于点O,若∠COB=120°,AB=6,则对角线BD= .
13.(2022春•二道区期末)如图,矩形ABCD中,对角线AC与BD相交于点O,AE垂直平分线度OB,垂足为点E,若BD=15,则AB= .
14.(2022春•洛江区期末)如图,在矩形ABCD中,AE平分∠BAD交BC于点E,AD=8cm,CE=3cm,则AB= cm.
15.(2022春•盐都区期中)如图,在矩形ABCD中,AB=3,对角线AC的长为5,作AC的垂直平分线交BC于点M,连接AM,则△ABM的周长为 .
16.(2022•南京模拟)如图,矩形ABCD的对角线AC,BD相交于点O,OF⊥AB,垂足为点F,BE⊥AC,垂足为点E,且E是OC的中点.若OF=2,则BD的长为 .
17.(2022春•上犹县期末)如图,矩形ABCD中,已知:AB=3,AD=5,点P是BC上一点,且△PAD是等腰三角形,则BP= .
18.(2022春•邗江区校级月考)点P在矩形ABCD内部,当点P到矩形的一条边的两个端点距离相等时,称点P为该边的“和谐点”.如图,点P在矩形ABCD内部,且AB=10,BC=6.若P是边AD的“和谐点”,连接PA,PB,PD,则tan∠PAB•tan∠PBA的最小值为 .
三、解答题(本大题共6小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2022春•前郭县期末)如图,矩形ABCD的对角线AC、BD相交于点O,AE⊥BD,垂足为E,∠AOB=56°,求∠EAB的度数.
20.(2022春•玉州区期末)如图,矩形ABCD的对角线AC、BD相交于点O,点E、F在BD上,OE=OF.
(1)求证:AE=CF.
(2)若AB=2,∠AOD=120°,求矩形ABCD的面积.
21.(2022春•铜官区期末)如图1,矩形ABCD中,AB=2,BC=3,过对角线AC中点O的直线分别交边BC、AD于点E、F
(1)求证:四边形AECF是平行四边形;
(2)如图2,当EF⊥AC时,求EF的长度.
22.(2021春•柳南区校级期末)如图,矩形ABCD的对角线AC、BD相交于点O,点E、F在AC上,AE=CF.
(1)求证:四边形BEDF是平行四边形;
(2)若AD=2,∠AOB=120°,求AB的长.
23.(2022秋•莲湖区校级月考)已知,在长方形ABCD中,AB=8,BC=6,点E,F分别是边AB,BC上的点,连接DE,DF,BP.
(1)如图1,当CF=2BE=2时,试说明△DEF是直角三角形;
(2)如图2,若点E是边AB的中点,DE平分∠ADF,求BF的长.
24.(2022春•嘉祥县期末)如图①,在矩形ABCD中,点E、F分别在AD、BC上,且AE=CF.直线EF分别交BA、DC的延长线于点G、H.
(1)求证:四边形BHDG是平行四边形;
(2)如图②,若四边形BHDG是菱形,且AB=4,BC=8,求CH的长.
专题18.5矩形的性质专项提升训练(重难点培优)
班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷满分120分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2022春•阜平县期末)如图,AC,BD是矩形ABCD的对角线,∠AOB=40°,则∠ACD的度数为( )
A.50°B.55°C.65°D.70°
【分析】根据矩形的性质可知,AC=BD,AO=CO,BO=DO,所以OC=OD,根据对顶角相等得到∠AOB=∠COD=40°,再利用等腰三角形的性质求得∠ACD的度数即可.
【解答】解:∵四边形ABCD是矩形,
∴AC=BD,AO=CO,BO=DO,
∴OC=OD,
∴∠OCD=∠ODC,
∵∠AOB=40°,
∴∠COD=40°,
∴∠OCD=∠ODC=70°.
故选:D.
2.(2022春•喀什地区期末)如图,在矩形ABCD中,∠BOC=120°,AC=2,则AB的长为( )
A.1B.2C.D.
【分析】由矩形的性质得出OA=OB=1,再证明△AOB是等边三角形,得出AB=OA即可.
【解答】解:∵四边形ABCD是矩形,AC=2,
∴OA=AC=1,OB=BD,AC=BD,
∴OA=OB=1,
∵∠BOC=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=1;
故选:A.
3.(2022春•覃塘区期末)在矩形ABCD中,若相邻的两边长分别是4和,则对角线所夹的锐角度数是( )
A.30°B.40°C.45°D.60°
【分析】根据矩形的性质得出∠ABC=90°,根据AB和BC的长求出AC,得出等边三角形AOB,即可求出对角线所夹的锐角度数.
【解答】解:如图,
∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD,AC=2AO,BD=2BO,
∵AB=4,BC=4,
∴在Rt△ABC中,由勾股定理得:AC===8,
∴AO=BO=×8=4,
∵AB=4,
∴△AOB是等边三角形,
∴∠AOB=60°,
即对角线所夹的锐角度数是60°.
故选:D.
4.(2022春•平泉市期末)求证:矩形的两条对角线相等.
已知:如图,四边形ABCD为矩形.求证:AC=BD.
以下是排乱的证明过程:
①∵BC=CB
②∴AB=CD,∠ABC=∠DCB
③∵四边形ABCD是矩形
④∴AC=DB
⑤∴△ABC≌△DCB
证明步骤正确的顺序是( )
A.①②③⑤④B.③①②⑤④C.①⑤②③④D.③②①⑤④
【分析】写出证明过程,由证明过程可以判断顺序.
【解答】解:∵四边形ABCD是矩形
∴AB=CD,∠ABC=∠DCB,
又∵BC=BC,
∴△ABC≌△DCB,
∴AC=BD,
故顺序为③②①⑤④.
故选:D.
5.(2022春•海口期末)如图,在矩形ABCD中,DE∥AC,CE∥BD.AC=4,则四边形OCED的周长为( )
A.6B.8C.10D.12
【分析】首先利用平行四边形的判定证明四边形ODEC为平行四边形,然后利用矩形的性质得到OD=OC=2即可求出四边形OCED的周长.
【解答】解:∵DE∥AC,CE∥BD,
∴四边形ODEC为平行四边形,
∴DE=OC,CE=OD,
∵四边形ABCD为矩形,
∴AC=BD,OD=OC=OA=OB,
∴OD=OC=2,
∴DE=CE=2,
∴四边形OCED的周长为8.
故选:B.
6.(2022春•长乐区期中)如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AD于E,若AB=4,BC=8,则AE的长为( )
A.3B.4C.5D.2
【分析】连接CE,根据矩形的对边相等可得AD=BC=8,CD=AB=4,根据矩形的对角线互相平分可得OA=OC,然后判断出OE垂直平分AC,再根据线段垂直平分线上的点到两端点的距离相等可得AE=CE,设AE=CE=x,表示出DE,然后在Rt△CDE中,利用勾股定理列出方程求解即可.
【解答】解:如图,连接CE,
在矩形ABCD中,
∵AB=4,BC=8,
∴AD=BC=8,CD=AB=4,OA=OC,
∵OE⊥AC,
∴OE垂直平分AC,
∴AE=CE,
设AE=CE=x,则DE=8﹣x,
在Rt△CDE中,CD2+DE2=CE2,
即42+(8﹣x)2=x2,
解得x=5,
即AE的长为5.
故选:C.
7.(2022春•静海区校级期中)如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC于E交AB于E,点G是AE的中点,且∠AOG=30°,OE=1,则下列结论:(1)DC=3OG;(2)OG=BC;(3)四边形AECF为菱形;(4)S△AOE=S四边形ABCD.其中正确的个数为( )
A.①②③B.①③④C.②③④D.①②④
【分析】根据条件,OG是直角△AOE斜边上的中线,且△FOC≌△EOA,然后利用三角函数求得BC、AB以及OA、OC之间的关系即可作出判断.
【解答】解:∵EF⊥AC,G是AF的中点,
∴AG=OG=GF,
∴∠OAF=∠AOG=30°,
在直角△ABC中,∠CAB=30°,
∴BC=AC=OC,设BC=a,AC=2a,AO=OC=a.
AE=a,AB=a,OG=a,
∴CD=AB=3OG,故①正确;
OG=a≠a=BC,故②错误;
∵∠FCO=∠EAO,∠CFO=∠AEO,OA=OC,
∴△FOC≌△EOA(AAS),
∴OE=OF,
又∵AO=OC,EF⊥AC,
∴四边形AFCE是菱形,故③正确;
∵S△AOE=a•a=a2,S矩形ABCD=a•a=a2,
∴S△AOE=S矩形ABCD,故④正确.
故选:B.
8.(2022•荣昌区自主招生)如图,在矩形ABCD中,对角线AC,BD相交于点O,∠DAC=60°,点F在线段AO上,连接DF,以DF为边作等边三角形DFE,点E和点A分别位于DF两侧,下列结论:①DO=DA;②DF=EC;③∠ADF=∠ECF;④∠BDE=∠EFC中正确结论的序号为( )
A.①④B.①②③C.②③④D.①②③④
【分析】①根据∠DAC=60°,OD=OA,得出△OAD为等边三角形,即可得出结论①正确;
②如图,连接OE,利用SAS证明△DAF≌△DOE,再证明△ODE≌△OCE,即可得出结论②正确;
③通过等量代换即可得出结论③正确;
④根据△DAO,△DEF是等边三角形可以证明∠EFC=∠ADF,然后根据②∠ADF=∠BDE,等量代换即可得到∠BDE=∠EFC.
【解答】解:①在矩形ABCD中,对角线AC,BD相交于点O,
∵∠DAC=60°,OD=OA,
∴△OAD为等边三角形,
∴∠DOA=∠DAO=∠ODA=60°,AD=OD,故①正确,
②连接OE.
∵△DFE为等边三角形,
∴∠EDF=∠EFD=∠DEF=60°,DF=DE,
∵∠BDE+∠FDO=∠ADF+∠FDO=60°,
∴∠BDE=∠ADF,
∵∠ADF+∠AFD+∠DAF=180°,
∴∠ADF+∠AFD=180°﹣∠DAF=120°,
∵∠EFC+∠AFD+∠DFE=180°,
∴∠EFC+∠AFD=180°﹣∠DFE=120°,
∴∠ADF=∠EFC,
∴∠BDE=∠EFC,
在△DAF和△DOE中,
,
∴△DAF≌△DOE(SAS),
∴∠DOE=∠DAF=60°,
∵∠COD=180°﹣∠AOD=120°,
∴∠COE=∠COD﹣∠DOE=120°﹣60°=60°,
∴∠COE=∠DOE,
在△ODE和△OCE中,
,
∴△ODE≌△OCE(SAS),
∴ED=EC=DF,故②正确;
③∵∠ODE=∠ADF,
∴∠ADF=∠OCE,即∠ADF=∠ECF,
故结论③正确;
④∵△DAO,△DEF是等边三角形,
∴∠DAO=∠DFE=60°,
∴∠EFC+∠AFD=∠ADF+∠AFD=120°,
∴∠EFC=∠ADF,
根据②知∠ADF=∠BDE,
∴∠BDE=∠EFC.
故④正确.
故选:D.
9.(2022秋•章丘区期中)如图,在矩形ABCD中,AB=24,BC=12,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形.则AE的长是( )
A.15B.20C.D.
【分析】连接EF交AC于点O,连接CE,根据菱形的性质可得CF=CE,证明△CFO≌△AEO,可得CF=AE,再根据勾股定理可得CE的长,进而可得结论.
【解答】解:如图,连接EF交AC于点O,连接CE,
∵四边形EGFH是菱形,
∴EF⊥GH,OE=OF,
∴CF=CE,
在△CFO和△AEO中,
,
∴△CFO≌△AEO(AAS),
∴CF=AE,
∴CE=AE,
∴BE=AB﹣AE=24﹣CE,
在Rt△CEB中,根据勾股定理,得
CE2=BE2+BC2,
∴CE2=(24﹣CE)2+122,
解得CE=15.
∴AE=15.
故选:A.
10.(2022秋•姜堰区期中)如图,在矩形ABCD中,AB=3cm,BC=cm,点P从A点出发沿AB以cm/s的速度向点B运动,当PA=PC时,点P运动的时间为( )
A.sB.2sC.10sD.10s或2s
【分析】设点P运动的时间为ts,根据题意得:AP=tcm,PC==tcm,PB=AB﹣AP=(3﹣t)cm,然后根据勾股定理列方程求解即可.
【解答】解:设点P运动的时间为ts,
根据题意得:AP=tcm,
∴PC==tcm,
∵PB=AB﹣AP=(3﹣t)cm,
∴PC2=BC2+PB2,
∴t2=2+(3﹣t)2,
解得t=2或t=10(舍去),
∴点P运动的时间为2s,
故选:B.
二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上
11.(2022春•费县期末)如图所示.在矩形ABCD中,AB=2.BD=4,则∠AOD= 120 度.
【分析】根据矩形的性质可知OA=OB,OB=BD,证得OB=OA=AB=2,所以△AOB是等边三角形,得出∠AOB=60°,则∠AOD=120°.
【解答】解:∵四边形ABCD是矩形,
∴AC=BD,OA=AC,OB=BD,
∴OA=OB,
∵BD=4,AB=2,
∴OB=OA=AB=2,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴∠AOD=120°.
故答案为:120.
12.(2022春•仙居县期末)如图,矩形ABCD中,AC与BD交于点O,若∠COB=120°,AB=6,则对角线BD= 12 .
【分析】根据矩形性质求出BD=2OB,OA=OB,求出∠AOB=60°,得出等边△AOB,求出OB=AB,即可求出答案.
【解答】解:∵四边形ABCD是矩形,
∴BD=2OB,AC=2OA,AC=BD,
∴OA=OB,
∵∠BOC=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB=6,
∴BD=2OB=12,
故答案为:12.
13.(2022春•二道区期末)如图,矩形ABCD中,对角线AC与BD相交于点O,AE垂直平分线度OB,垂足为点E,若BD=15,则AB= 7.5 .
【分析】首先利用矩形的性质得到OA的长度,然后利用线段的垂直平分线的性质得到AB=OB=OA即可求解.
【解答】解:∵矩形ABCD中,对角线AC与BD相交于点O,
∴AO=OB=OC=OD,
而BD=15,
∴OB=OA=BD=7.5,
∵AE垂直平分线段OB,
∴AB=OA,
∴AB=OB=OA,
∴AB=7.5.
故答案为:7.5.
14.(2022春•洛江区期末)如图,在矩形ABCD中,AE平分∠BAD交BC于点E,AD=8cm,CE=3cm,则AB= 5 cm.
【分析】首先利用矩形的性质得到可以证明∠DAE=∠BEA,然后利用角平分线的性质证明∠BAE=∠BEA,接着利用等腰三角形的判定得到AB=BE即可求解.
【解答】解:∵四边形ABCD为矩形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD交BC于点E,
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AD=8cm,CE=3cm,
∴BC=8,
∴AB=BE=BC﹣CE=8﹣3=5cm.
故答案为:5.
15.(2022春•盐都区期中)如图,在矩形ABCD中,AB=3,对角线AC的长为5,作AC的垂直平分线交BC于点M,连接AM,则△ABM的周长为 7 .
【分析】由勾股定理可求BC的长,由线段垂直平分线的性质可得AM=CM,可求解.
【解答】解:∵四边形ABCD是矩形,
∴∠B=90°,
∴BC===4,
∵AC的垂直平分线交BC于点M,
∴AM=CM,
∴△ABM的周长=AB+BM+AM=AB+BC=7,
故答案为:7.
16.(2022•南京模拟)如图,矩形ABCD的对角线AC,BD相交于点O,OF⊥AB,垂足为点F,BE⊥AC,垂足为点E,且E是OC的中点.若OF=2,则BD的长为 8 .
【分析】根据矩形的性质可以得到OC=OB,再根据BE⊥AC及E点为CO的中点,根据线段垂直平分线的性质证得△CBO是等边三角形,从而得到∠DBA=30°,然后根据30°直角三角形的性质求得BO长,BD=2BO,即可得出答案.
【解答】解:∵BE⊥AC,E点为CO的中点,
∴BE垂直平分OC,
∴BC=OB,
∵四边形ABCD是矩形,
∴AC=BD,OC=OA,OD=OB,∠CBA=90°,
∴OC=OB,
∴CB=BO=CO,
∴△OBC是等边三角形,
∴∠CBD=60°,
∴∠DBA=30°,
∵OF⊥AB,OF=2,
∴BO=2OF=4,
∵O点为BD中点,
∴BD=2BO=8.
故答案为:8.
17.(2022春•上犹县期末)如图,矩形ABCD中,已知:AB=3,AD=5,点P是BC上一点,且△PAD是等腰三角形,则BP= 1或4或2.5 .
【分析】根据矩形的性质可知DC=AB=3,AD=BC=5,再根据△PAD是等腰三角形的性质可得DP=AD=5,勾股定理可得CP的长度,则BP=BC﹣CP,即可求得BP的长度.
【解答】解:①当DP=AD时,
∵矩形ABCD,
∴DC=AB=3,AD=BC=5,
∵△PAD是等腰三角形,
∴DP=AD=5,
在Rt△PCD中,
PC==4,
∴BP=BC﹣CP=5﹣4=1.
②当AD=AP时,
∴AP=AD=5,
在Rt△ABP中,
由勾股定理得,
BP==4,
③当AP=DP时,
过P作PE⊥AD于点E,
∴AE=AD=2.5,
∵∠B=∠BAE=∠AEP=90°,
∴四边形ABPE是矩形,
∴BP=AE=2.5.
综上所述,BP=1或4或2.5.
故答案为:1或4或2.5.
18.(2022春•邗江区校级月考)点P在矩形ABCD内部,当点P到矩形的一条边的两个端点距离相等时,称点P为该边的“和谐点”.如图,点P在矩形ABCD内部,且AB=10,BC=6.若P是边AD的“和谐点”,连接PA,PB,PD,则tan∠PAB•tan∠PBA的最小值为 .
【分析】过点P作PN⊥AB于N,tan∠PAB•tan∠PBA=•=,设AN=x,则BN=10﹣x,求出AN•BN有最大值25,即可求得tan∠PAB•tan∠PBA的最小值是.
【解答】解:过点P作PN⊥AB于N,如图:
∵点P是边AD的“和谐点”,
∴PA=PD,
∴PN=BC=3,
∴tan∠PAB=,tan∠PBA=,
∴tan∠PAB•tan∠PBA=•=,
设AN=x,则BN=10﹣x,
∴AN•BN=x(10﹣x)=﹣(x﹣5)2+25,
当x=5时,AN•BN有最大值25,
∴有最小值,
∴tan∠PAB•tan∠PBA的最小值是.
三、解答题(本大题共6小题,共66分.解答时应写出文字说明、证明过程或演算步骤)
19.(2022春•前郭县期末)如图,矩形ABCD的对角线AC、BD相交于点O,AE⊥BD,垂足为E,∠AOB=56°,求∠EAB的度数.
【分析】根据矩形的性质可知OA=OB,根据∠AOB的度数求出∠ABO的度数,然后根据直角三角形的锐角互余求解即可.
【解答】解:∵四边形ABCD是矩形,
∴,
∴AO=OB,
又∵∠AOB=56°,
∴∠OBA=∠OAB=62°,
∵AE⊥BD,
∴∠BAE=90°﹣∠ABE=28°.
20.(2022春•玉州区期末)如图,矩形ABCD的对角线AC、BD相交于点O,点E、F在BD上,OE=OF.
(1)求证:AE=CF.
(2)若AB=2,∠AOD=120°,求矩形ABCD的面积.
【分析】(1)由矩形的性质得出OA=OC,OB=OD,AC=BD,∠ABC=90°,证出OE=OF,由SAS证明△AOE≌△COF,即可得出AE=CF;
(2)证出△AOB是等边三角形,得出OA=AB=3,AC=2OA=6,在Rt△ABC中,由勾股定理求出BC,即可得出矩形ABCD的面积.
【解答】解:(1)证明:∵四边形ABCD是矩形
∴OA=OC,
在△AOE和△COF
∵,
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)∵四边形ABCD是矩形
∴AC=BD
∵,
∴AO=DO
∴
∴在Rt△ADB中,BD=2AB=4,
∴
∴矩形ABCD的面积=.
21.(2022春•铜官区期末)如图1,矩形ABCD中,AB=2,BC=3,过对角线AC中点O的直线分别交边BC、AD于点E、F
(1)求证:四边形AECF是平行四边形;
(2)如图2,当EF⊥AC时,求EF的长度.
【分析】(1)证明△AOF≌△COE全等,可得AF=EC,∵AF∥EC,∴四边形AECF是平行四边形;
(2)由(1)知四边形AECF是平行四边形,且EF⊥AC,∴四边形AECF为菱形,假设BE=a,根据勾股定理求出a,从而得知EF的长度;
【解答】解:∵矩形ABCD,∴AF∥EC,AO=CO
∴∠FAO=∠ECO
∴在△AOF和△COE中,,
∴△AOF≌△COE(ASA)
∴AF=EC
又∵AF∥EC
∴四边形AECF是平行四边形;
(2)由(1)知四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF为菱形,
设BE=a,则AE=EC=3﹣a
∴a2+22=(3﹣a)2
∴a=
则AE=EC=,
∵AB=2,BC=3,
∴AC==
∴AO=OC=,
∴OE===,
∴EF=2OF=.
22.(2021春•柳南区校级期末)如图,矩形ABCD的对角线AC、BD相交于点O,点E、F在AC上,AE=CF.
(1)求证:四边形BEDF是平行四边形;
(2)若AD=2,∠AOB=120°,求AB的长.
【分析】(1)根据平行四边形的判定即可求出答案.
(2)根据矩形的性质以及含30度角的直角三角形的性质即可求出答案.
【解答】解:(1)在矩形ABCD中,
∴OA=OB=OC=OD,
∵AE=CF,
∴OE=OF,
∴四边形BEDF是平行四边形.
(2)由(1)可知:OA=OB,
∵∠AOB=120°,
∴∠DBA=30°,
∵AD=2,
∴AB=AD=6.
23.(2022秋•莲湖区校级月考)已知,在长方形ABCD中,AB=8,BC=6,点E,F分别是边AB,BC上的点,连接DE,DF,BP.
(1)如图1,当CF=2BE=2时,试说明△DEF是直角三角形;
(2)如图2,若点E是边AB的中点,DE平分∠ADF,求BF的长.
【分析】(1)在Rt△ADE中,DE2=AE2+AD2=62+72=85,在Rt△DCF中,DF2=DC2+CF2=82+22=68,在Rt△BEF中,EF2=BE2+BF2=12+42=17,得出DF2+EF2=DE2,即可得出结论;
(2)作EH⊥DF于H,则∠A=∠DHE=90°,证明△AED≌△HED(AAS),得出DA=DH=6,EA=EH=4,得出EH=EB=4,证明Rt△EHF≌Rt△EBF(HL),得出BF=HF.设BF=x,则HF=x,CF=6﹣x,得出DF=DH+HF=6+x,在Rt△CDF中,由勾股定理得出方程,解方程即可.
【解答】(1)证明;∵CF=2BE=2,
∴BE=1,
∴AE=AB﹣BE=7.
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,CD=AB=8,AD=BC=6,
在Rt△ADE中,DE2=AE2+AD2=62+72=85,
在Rt△DCF中,DF2=DC2+CF2=82+22=68,
在Rt△BEF中,EF2=BE2+BF2=12+42=17,
∴DF2+EF2=DE2,
∴△DEF是直角三角形,且∠DFE=90°;
(2)解:作EH⊥DF于H,
则∠A=∠DHE=90°.
∵DE平分∠ADF,
∴∠ADE=∠HDE,
在△AED和△HED中,
,
∴△AED≌△HED(AAS),
∴DA=DH=6,EA=EH=4,
∴EH=EB=4,
在Rt△EHF和Rt△EBF中,
,
∴Rt△EHF≌Rt△EBF(HL),
∴BF=HF.
设BF=x,则HF=x,CF=6﹣x,
∴DF=DH+HF=6+x,
在Rt△CDF中,DC2+CF2=DF2,
∴82+(6﹣x)2=(6+x)2,
∴x=,
即BF=.
24.(2022春•嘉祥县期末)如图①,在矩形ABCD中,点E、F分别在AD、BC上,且AE=CF.直线EF分别交BA、DC的延长线于点G、H.
(1)求证:四边形BHDG是平行四边形;
(2)如图②,若四边形BHDG是菱形,且AB=4,BC=8,求CH的长.
【分析】(1)由“AAS”证△AGE≌△CHF,得AG=CH,即可解决问题;
(2)由菱形的性质得BH=DH=4+CH,再由勾股定理得BH2=BC2+CH2,即(4+CH)2=82+CH2,求解即可.
【解答】(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,∠BAD=∠BCD=90°,
∴∠AGE=∠CHF,∠GAE=∠HCF=90°,
在△AGE和△CHF中,
,
∴△AGE≌△CHF(AAS),
∴AG=CH,
∴AB+AG=CD+CH,
即BG=DH,
∵AB∥CD
∴四边形BHDG是平行四边形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=4,
∵四边形BHDG是菱形,
∴BH=DH=4+CH,
在Rt△BCH中,由勾股定理得:BH2=BC2+CH2,
即(4+CH)2=82+CH2,
解得:CH=6,
即CH的长为6.
初中数学人教版八年级下册第二十章 数据的分析20.3 体质健康测试中的数据分析课后测评: 这是一份初中数学人教版八年级下册<a href="/sx/tb_c10270_t7/?tag_id=28" target="_blank">第二十章 数据的分析20.3 体质健康测试中的数据分析课后测评</a>,共24页。试卷主要包含了3方差专项提升训练,5,则说法错误的是,5 ,c= 6 ,d= 1等内容,欢迎下载使用。
数学八年级下册20.1.1平均数一课一练: 这是一份数学八年级下册<a href="/sx/tb_c102665_t7/?tag_id=28" target="_blank">20.1.1平均数一课一练</a>,共20页。试卷主要包含了1平均数专项提升训练,5%D.95%,5元B.30,85千米C.2,0、9,75分,2+57,2+27等内容,欢迎下载使用。
初中人教版18.2.3 正方形同步达标检测题: 这是一份初中人教版<a href="/sx/tb_c88745_t7/?tag_id=28" target="_blank">18.2.3 正方形同步达标检测题</a>,共30页。试卷主要包含了7正方形专项提升训练,5°C.20°D.10°等内容,欢迎下载使用。













