高中数学第八章 立体几何初步8.6 空间直线、平面的垂直第一课时复习练习题

这是一份高中数学第八章 立体几何初步8.6 空间直线、平面的垂直第一课时复习练习题，共8页。

[A组 必备知识练]
1．一条直线和三角形的两边同时垂直，则这条直线和三角形的第三边的位置关系是( )
A．平行 B．垂直
C．相交但不垂直 D．相交且垂直
解析：如图，l⊥AB，l⊥AC⇒l⊥平面ABC⇒l⊥BC.
答案：B
2．如图所示，若斜线段AB是它在平面α上的射影BO的2倍，则AB与平面α所成的角是( )
A．60° B．45°
C．30° D．120°
解析：∠ABO即是斜线AB与平面α所成的角．在Rt△AOB 中，AB＝2BO，
所以cs ∠ABO＝ eq \f(1,2)，即∠ABO＝60°.
答案：A
3.在正四棱锥P­ABCD中，AB＝2，PA＝2，则点P到平面ABCD的距离为( )
A．1 B． eq \r(2)
C． eq \r(3) D．2
解析：设底面中心为O，连接PO，OA.
由已知得PO⊥平面ABCD，
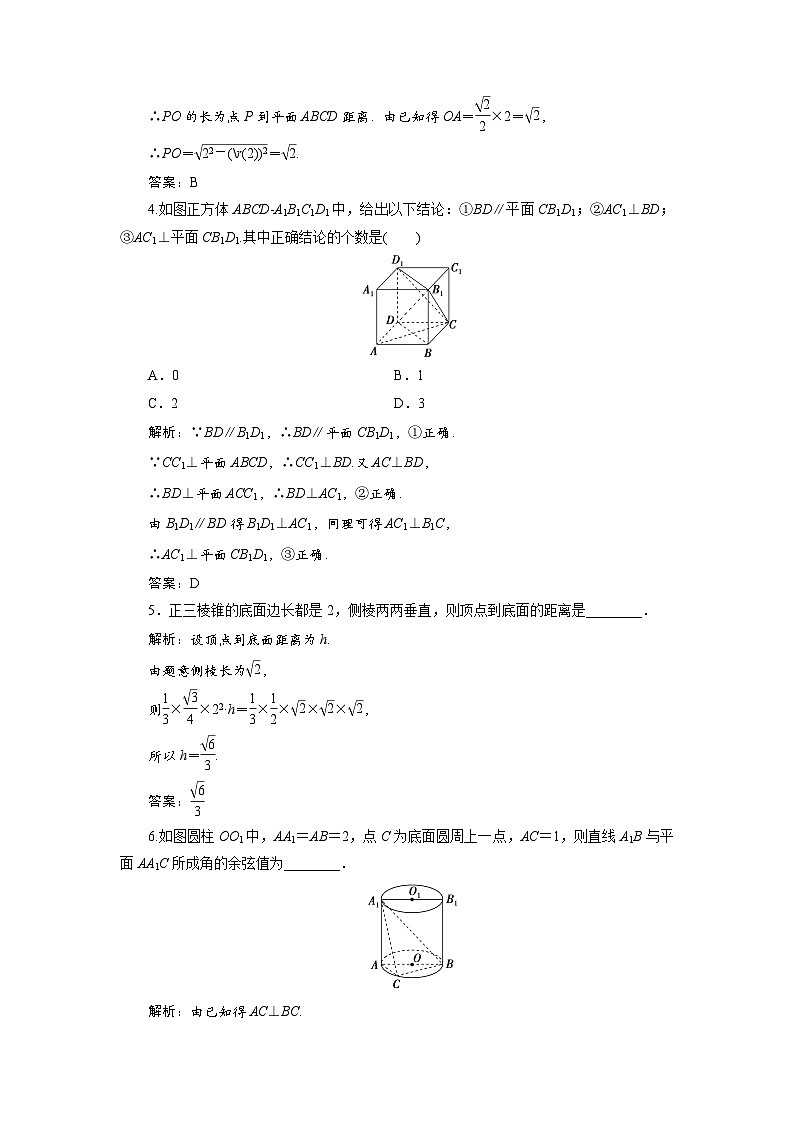
∴PO的长为点P到平面ABCD距离．由已知得OA＝ eq \f(\r(2),2)×2＝ eq \r(2)，
∴PO＝ eq \r(22－(\r(2))2)＝ eq \r(2).
答案：B
4.如图正方体ABCD­A1B1C1D1中，给出以下结论：①BD∥平面CB1D1；②AC1⊥BD；③AC1⊥平面CB1D1.其中正确结论的个数是( )
A．0 B．1
C．2 D．3
解析：∵BD∥B1D1，∴BD∥平面CB1D1，①正确．
∵CC1⊥平面ABCD，∴CC1⊥BD.又AC⊥BD，
∴BD⊥平面ACC1，∴BD⊥AC1，②正确．
由B1D1∥BD得B1D1⊥AC1，同理可得AC1⊥B1C，
∴AC1⊥平面CB1D1，③正确．
答案：D
5．正三棱锥的底面边长都是2，侧棱两两垂直，则顶点到底面的距离是________．
解析：设顶点到底面距离为h.
由题意侧棱长为 eq \r(2)，
则 eq \f(1,3)× eq \f(\r(3),4)×22·h＝ eq \f(1,3)× eq \f(1,2)× eq \r(2)× eq \r(2)× eq \r(2)，
所以h＝ eq \f(\r(6),3).
答案： eq \f(\r(6),3)
6.如图圆柱OO1中，AA1＝AB＝2，点C为底面圆周上一点，AC＝1，则直线A1B与平面AA1C所成角的余弦值为________．
解析：由已知得AC⊥BC.
又知AA1⊥底面ABC，∴AA1⊥BC.
又AC∩AA1＝A，∴BC⊥平面AA1C，
∴∠BA1C为A1B与平面AA1C所成的角．
∵AA1＝AB＝2，∴A1B＝2 eq \r(2).
又AC＝1，∴A1C＝ eq \r(5)，
∴cs ∠BA1C＝ eq \f(\r(5),2\r(2))＝ eq \f(\r(10),4)，
∴直线A1B与平面AA1C所成角的余弦值为 eq \f(\r(10),4).
答案： eq \f(\r(10),4)
7.如图，在正方体ABCD­A1B1C1D1中，上、下底面中心分别为O1，O，求O1B与平面AA1C1C所成角的余弦值．
解：连接BD，则BD∩AC＝O.
∵ABCD是正方形，∴BD⊥AC.
∵AA1⊥平面ABCD，
∴BD⊥AA1.
∵AA1，AC⊂平面AA1C1C，AA1∩AC＝A，
∴BD⊥平面AA1C1C，∴O1O为O1B在平面AA1C1C上的射影，
∴∠BO1O为O1B与平面AA1C1C所成的角．
设正方体的棱长为a，
∴BO＝ eq \f(1,2)BD＝ eq \f(\r(2),2)a.
∵OO1＝AA1＝a，
∴O1B＝ eq \r(a2＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)a))\s\up12(2))＝ eq \f(\r(6),2)a，
∴cs ∠BO1O＝ eq \f(a,\f(\r(6),2)a)＝ eq \f(\r(6),3)，
∴O1B与平面AA1C1C所成角的余弦值为 eq \f(\r(6),3).
8.如图，四棱锥P­ABCD的底面是边长为1的正方形，PA⊥CD，PA＝1，PD＝ eq \r(2).
(1)求证PA⊥平面ABCD；
(2)求四棱锥P­ABCD的体积．
(1)证明：由已知PA＝1，PD＝ eq \r(2)，AD＝1，
∴PA2＋AD2＝PD2，
∴PA⊥AD.
又PA⊥CD，AD，CD⊂平面ABCD，AD∩CD＝D，
∴PA⊥平面ABCD.
(2)解：由(1)知PA＝1为点P到平面ABCD的距离，即四棱锥P­ABCD的高．
又SABCD＝1，
∴VP­ABCD＝ eq \f(1,3)SABCD·PA＝ eq \f(1,3)×1×1＝ eq \f(1,3).
[B组 关键能力练]
9．(多选)过△ABC所在平面α外一点P，作PO⊥α，垂足为O，连接PA，PB，PC，则以下命题正确的是( )
A．若PA＝PB＝PC，则点O是△ABC的外心
B．若点P到直线AB，BC，CA的距离相等，则点O是△ABC的内心
C．若PA，PB，PC两两垂直，则点O是△ABC的垂心
D．若PA＝PB＝PC，∠C＝90°，则点O是AB边的中点
解析：如图，连接OA，OB，OC.
由PO⊥α，得PO⊥OA，PO⊥OB，PO⊥OC.
若PA＝PB＝PC，∴△POA≌△POB≌△POC，
∴OA＝OB＝OC，∴点O为△ABC的外心，选项A正确．
类同A，可得点O到直线AB，BC，CA距离相等，若点O在△ABC内部，则点O为△ABC的内心；
若O在△ABC外部，则点O为△ABC的旁心，选项B不正确．
若PA，PB，PC两两垂直，∴PA⊥平面PBC，∴PA⊥BC.又PO⊥BC，∴BC⊥平面POA，
∴BC⊥OA，同理CA⊥OB，AB⊥OC，∴点O为△ABC的垂心，选项C正确．
若PA＝PB＝PC，由选项A知点O为△ABC的外心．∵∠C＝90°，∴O为AB的中点，选项D正确．
答案：ACD
10.(多选)如图，在正方体ABCD­A1B1C1D1中，M，N分别为AC，A1B的中点，则下列说法中正确的是( )
A．MN∥平面ADD1A1
B．MN⊥AB
C．直线MN与平面ABCD所成角为45°
D．异面直线MN与DD1所成角为60°
解析：取AB的中点G，连接MG，NG，
取AA1，AD的中点E，F，连接EF.
可得MN∥EF⇒MN∥平面ADD1A1，A正确；
由题意可得AB⊥MG，AB⊥NG⇒AB⊥平面MNG⇒AB⊥MN，B正确；
由题意可得NG⊥平面ABCD，且NG＝MG⇒∠NMG＝45°，为所求角，C正确；
∠GNM为MN与DD1所成角，GNM＝45°，D不正确．
答案：ABC
11．如图，在各棱长均为2的正三棱柱ABC­A1B1C1中，M为A1C1的中点，则三棱锥M­AB1C的体积为________．
解析：∵在各棱长均为2的正三棱柱ABC­A1B1C1中，M为A1C1的中点，
∴B1M⊥A1C1.又CC1⊥平面A1B1C1，
B1M⊂平面A1B1C1，∴B1M⊥CC1.又∵A1C1，CC1⊂平面ACM，A1C1∩CC1＝C1，
∴B1M⊥平面ACM.又B1M＝ eq \r(3)，S△AMC＝ eq \f(1,2)×2×2＝2，
∴三棱锥M­AB1C的体积为 eq \f(1,3)×S△AMC×B1M＝ eq \f(1,3)×2× eq \r(3)＝ eq \f(2\r(3),3).
答案： eq \f(2\r(3),3)
12.如图，在三棱锥O­ABC中，三条棱OA，OB，OC两两垂直，且OA＝OB＝OC，M是AB的中点，则OM与平面ABC所成角的余弦值是________．
解析：不妨设OA＝OB＝OC＝1.∵OA，OB，OC两两垂直，∴AB＝BC＝AC＝ eq \r(2).
∵OB∩OC＝O，∴OA⊥平面OBC，S△ABC＝ eq \f(\r(3),4)·AB2＝ eq \f(\r(3),2).
设点O到平面ABC的距离为h.
∵V三棱锥O­ABC＝V三棱锥A­OBC，∴ eq \f(1,3)× eq \f(\r(3)h,2)＝ eq \f(1,3)× eq \f(1,2)×12×1，解得h＝ eq \f(\r(3),3).
又∵M是AB的中点，∴OM＝ eq \f(1,2)AB＝ eq \f(\r(2),2)，∴OM与平面ABC所成的角的正弦值为 eq \f(h,OM)＝ eq \f(\r(6),3)，∴OM与平面ABC所成角的余弦值为 eq \r(1－\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(6),3)))\s\up12(2))＝ eq \f(\r(3),3).
答案： eq \f(\r(3),3)
13.如图，已知AA1⊥平面ABC，BB1∥AA1，AB＝AC＝3，BC＝2 eq \r(5)，AA1＝ eq \r(7)，BB1＝2 eq \r(7)，点E和F分别为BC和A1C的中点．
(1)求证：EF∥平面A1B1BA；
(2)求直线A1B1与平面BCB1所成角的大小．
(1)证明：如图，连接A1B.在△A1BC中，因为点E和F分别是BC和A1C的中点，所以EF∥BA1.又EF⊄平面A1B1BA，BA1⊂平面A1B1BA，所以EF∥平面A1B1BA.
(2)解：如图，取BB1的中点M和B1C的中点N，连接A1M，A1N，NE.
因为N和E分别为B1C和BC的中点，所以NE∥B1B，NE＝ eq \f(1,2)B1B，故NE∥A1A且NE＝A1A，所以四边形NEAA1为平行四边形，所以A1N∥AE，且A1N＝AE.
因为AB＝AC，E为BC的中点，所以AE⊥BC，所以A1N⊥BC.
因为AA1⊥平面ABC，BB1∥AA1，则易证得BB1⊥平面ABC.因为AE⊂平面ABC，
所以BB1⊥AE，所以A1N⊥BB1.
又BB1∩BC＝B，所以A1N⊥平面BCB1，
从而∠A1B1N为直线A1B1与平面BCB1所成的角．
在△ABC中，可得AE＝2，所以A1N＝AE＝2.
因为BM∥AA1，BM＝AA1，所以四边形A1ABM为平行四边形，
所以A1M∥AB，A1M＝AB.
又AB⊥BB1，所以A1M⊥BB1.
在Rt△A1MB1中，可得A1B1＝ eq \r(B1M2＋A1M2)＝4.
在Rt△A1NB1中，sin ∠A1B1N＝ eq \f(A1N,A1B1)＝ eq \f(1,2)，因此∠A1B1N＝30°，
所以直线A1B1与平面BCB1所成角的大小为30°.
[C组 素养培优练]
14．如图，正方体ABCD­A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，则下列结论中正确结论的序号有________.
①AC⊥BE；
②直线AE与平面DBB1D1所成角的正弦值为定值 eq \f(1,3)；
③当EF为定值时，三棱锥E­ABF的体积为定值；
④异面直线AE，BF所成角的余弦值为定值 eq \f(\r(6),3).
解析：连接BD，交AC于点O，连接EO.由正方体的性质，得AC⊥平面DBB1D1，而BE⊂平面DBB1D1，所以AC⊥BE，故①正确．
由AC⊥平面DBB1D1，
得OE是AE在平面DBB1D1上的射影，
所以∠AEO是直线AE与平面DBB1D1所成的角，因为AE不是定值，故②不正确．
由于点B到直线B1D1的距离不变，故△BEF的面积为定值，又点A到平面BEF的距离为 eq \f(\r(2),2)，故三棱锥E­ABF的体积为定值，故③正确．
当点E在点D1，点F在点B1时，异面直线AE与BF所成的角为 eq \f(π,4)，故④不正确．
答案：①③