

海南省省直辖县级行政单位2023-2024学年八年级上学期1月期末数学试题
展开全卷满分120分 完成时间100分钟
一、选择题(本大题满分36分,每小题3分)
在下列各题的四个备选答案中,只有一个是正确的,请将其正确选项的字母代号,用2B铅笔在答题卡对应的位置涂黑.
1.下列图案中,是轴对称图形的是( )
A.B.C.D.
2.下列运算错误的是( )
A.B.C.D.
3.中国信通院预计未来2~3年内将实现5G的个人终端应用和数字内容的创新突破,预计2025年全球5G移动用户数将突破23000000000户数据23000000000用科学记数法表示为( )
A.B.C.D.
4.下列变形从左到右是因式分解且因式分解正确的是( )
A.B.
C.D.
5.如图1是一个平分角的仪器,其中,,将点A放在角的顶点上,AB和AD沿着角的两边放下,沿AC画一条射线AE,则射线AE就是这个角的平分线.在这个操作过程中,运用了三角形全等的判定方法是( )
图1
A.SSSB.SASC.ASAD.AAS
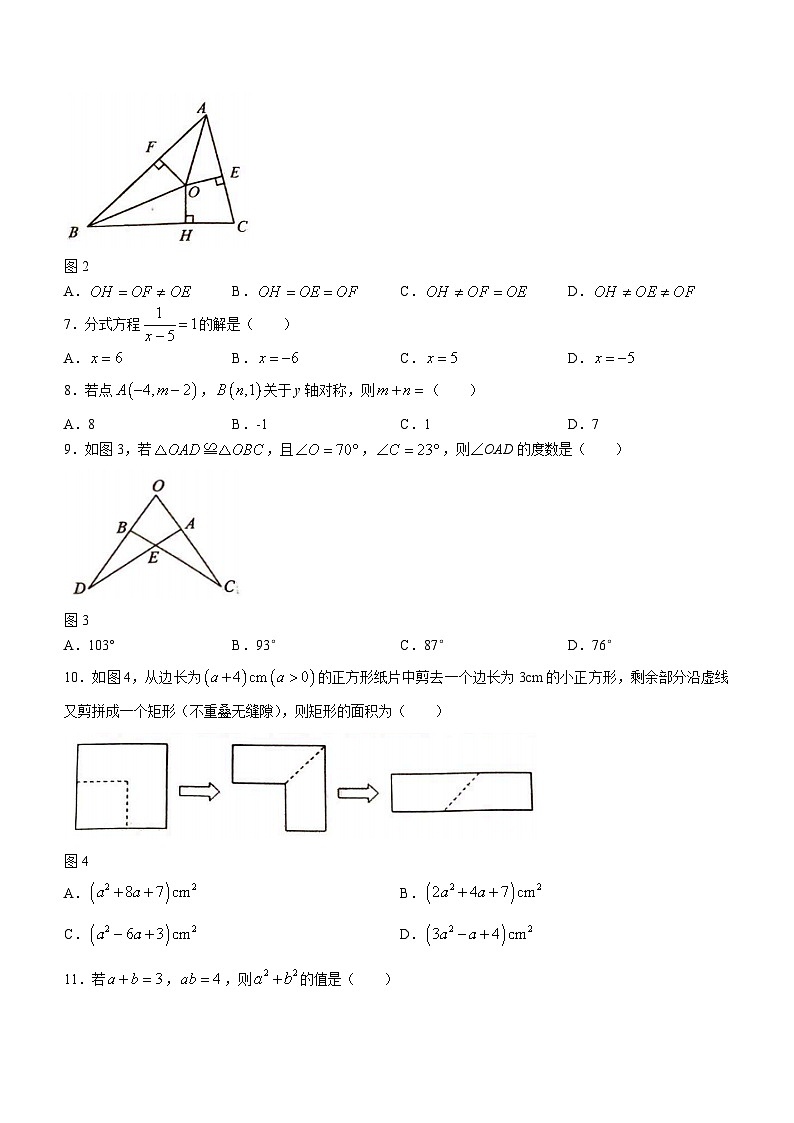
6.如图2,BO,AO分别是中∠ABC,∠BAC的平分线,,,,垂足分别为H,E,F,则OH,OE,OF长度的大小关系是( )
图2
A.B.C.D.
7.分式方程的解是( )
A.B.C.D.
8.若点,关于y轴对称,则( )
A.8B.-1C.1D.7
9.如图3,若,且,,则∠OAD的度数是( )
图3
A.103°B.93°C.87°D.76°
10.如图4,从边长为的正方形纸片中剪去一个边长为3cm的小正方形,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( )
图4
A.B.
C.D.
11.若,,则的值是( )
A.1B.2C.D.5
12.如图5,在等边中,BD是AC边上的高,点E在BC的延长线上,,则BE的长为( )
图5
A.4.5B.5C.6D.9
二、填空题(本大题满分12分,每小题3分)
13.若分式的值为0,则x的值为______.
14.如图6,已知,要证明还需添加的一个条件是______.(只填一个条件即可)
图6
15.已知关于x的多项式是一个完全平方式,则常数m的值为______.
16.如图7,在中,,,,动点P从点A出发在AB边上沿方向匀速运动,速度为,动点Q从点B出发在BC边上沿方向匀速运动,速度为.当点P到达点B时,P,Q两点同时停止运动,则当点P运动______秒时,为直角三角形.
图7
三、解答题(本大题满分72分)
17.(本题满分12分)计算:
(1)(2)
18.(本题满分10分)因式分解:
(1);(2).
19.(本题满分12分)先化简,再求值:,其中.
20.(本题满分12分)港珠澳大桥是世界上最长的跨海大桥,是被誉为“现代世界七大奇迹”超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.港珠澳大桥开通前从香港到珠海的车程为180千米,开通后的车程缩短了130千米,行驶时间仅为原来行驶时间的,已知港珠澳大桥开通后从香港到珠海的平均时速比开通前的平均时速多40千米.
(1)港珠澳大桥开通后,
①从香港到珠海的车程为______千米;
②开通后的行驶时间=开通前的行驶时间×______;
(2)求港珠澳大桥开通后从香港到珠海的平均速度是多少?
21.(本题满分12分)如图8,在长方形纸片ABCD中,点P在BC边上,将沿DP折叠,点C落在点E处,PE,DE分别交AB于点G,F,且.
(1)求证:;
(2)若,求BF的长.
图8
22.(本题满分14分)在平面直角坐标系中,点A,B分别是x轴、y轴上的动点,连接AB作等腰直角三角形ABC且.
(1)当点B在y轴负半轴上时,
①如图9-1,若∠OAB=20°,则______度;
②如图9-2,BC交x轴于点E,轴与AB交于点F,若,求证:AD平分∠BAC;
(2)如图9-3,当点B在y轴正半轴上且时,若,取点,连接CP,CP交x轴于点Q.当点B运动时,OQ的长度是否发生改变?若改变,请求出它的变化范围;若不变,求出它的长度.
2023-2024学年度第一学期八年级数学(上册)期末答案
一、选择题(本大题满分36分,每小题3分)
CBCD ABAD CAAC
二、填空题(本大题满12分,每小题3分)
13.2; 14.(或); 15.±6; 16.10或16
三、解答题(本大题满分72分)
17.(本题满分12分)
解:(1)原式
(2)原式
18.(本题满分10分)
解:(1)原式
(2)原式
19.(本题满分12分)
解:原式
当时,原式
20.(本题满分12分)
(1)①50;②
(2)解:设港珠澳大桥开通后从香港到珠海的平均速度是x千米时,根据题意得:
解得
经检验,是原分式方程的解.
答:港珠澳大桥开通后从香港到珠海的平均速度是100千米时.
21.(本题满分12分)
(1)证明:∵长方形纸片ABCD,∴
由折叠的性质得,,∴
在和中
∴(AAS)
(2)解:由得
∵,∴
由折叠的性质得,,∴
22.(本题满分14分)
(1)20;
(2)证明:∵轴,∴轴,∴
∵,
∴,∴
∵是等腰直角三角形且
∴,
在和中,
∴(ASA),∴
∵,∴即
∵,∴AD垂直平分CF
∴,∴AD平分∠BAC
(3)解:OQ的长度不变,.
过点C作轴于点H,如图所示
∴,∴
∵,∴,∴
在和中
∴(AAS),
∴,
∵,∴,∴
∵,∴
∴
∵,∴,∴
海南省省直辖县级行政单位澄迈县2023-2024学年八年级上学期期末数学试题: 这是一份海南省省直辖县级行政单位澄迈县2023-2024学年八年级上学期期末数学试题,共6页。试卷主要包含了单项选择题,填空题,解答题等内容,欢迎下载使用。
海南省省直辖县级行政单位澄迈县2023-2024学年八年级上学期期末数学试题(含答案): 这是一份海南省省直辖县级行政单位澄迈县2023-2024学年八年级上学期期末数学试题(含答案),共6页。试卷主要包含了单项选择题,填空题,解答题等内容,欢迎下载使用。
海南省省直辖县级行政单位东方市2023-2024学年八年级上学期期末数学试题(无答案): 这是一份海南省省直辖县级行政单位东方市2023-2024学年八年级上学期期末数学试题(无答案),共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












