上海市民办上宝中学2022-2023学年八年级下学期五月月考物理试卷

这是一份上海市民办上宝中学2022-2023学年八年级下学期五月月考物理试卷，共37页。试卷主要包含了选择题，填空题，综合题等内容，欢迎下载使用。
一、选择题（共30分）
1．（2分）已知空气密度为1.3千克/米3，你估算一下目前所在的教室中空气质量最接近（ ）
A．3千克B．30千克C．300千克D．3000千克
2．（2分）下列现象中，能说明分子在不停地做无规则运动的是（ ）
A．春天，落樱缤纷B．夏天，茉莉飘香
C．秋天，黄沙扑面D．冬天，雪花飘飘
3．（2分）小明比较”测物质密度”和“探究物质质量与体积关系”两个实验后，认为：
①所测的物理量相同；
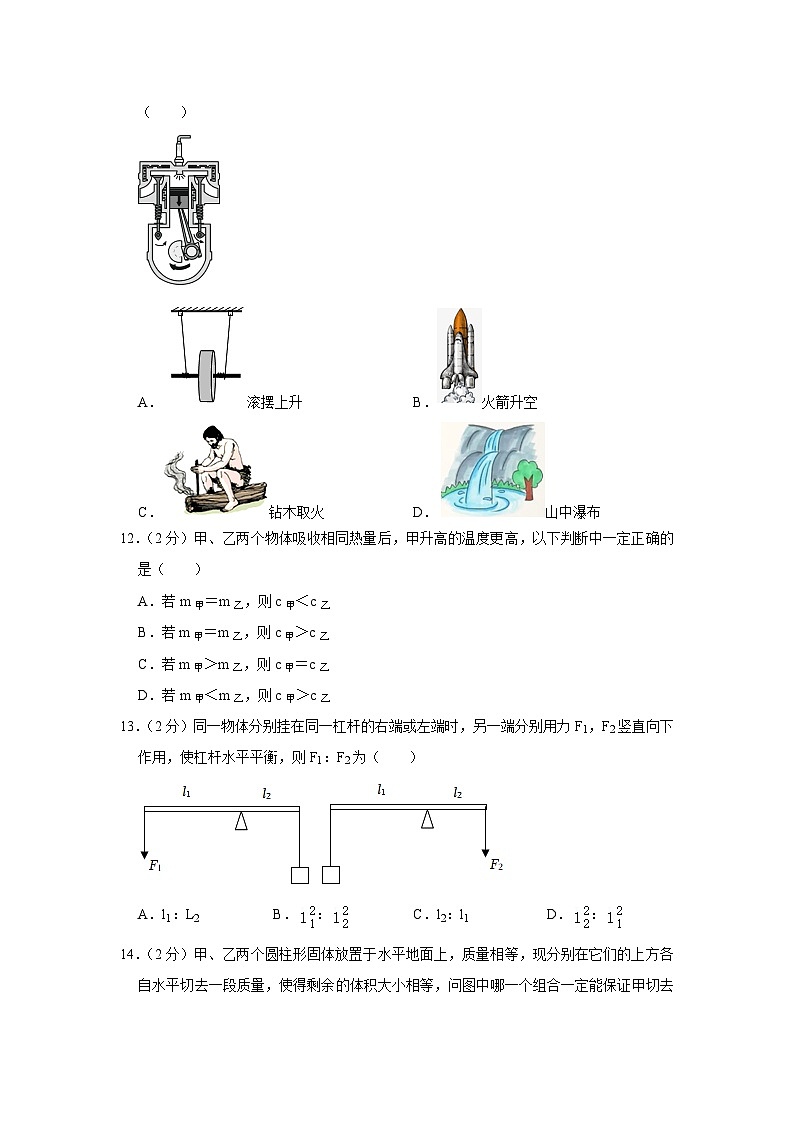
②测量的工具相同；
③多次测量的目的相同。
他的判断正确的是（ ）
A．①和②B．②和③C．①和③D．①、②和③
4．（2分）下列各物理量可用来鉴别物质的是（ ）
①温度；
②密度；
③内能；
④比热容。
A．①②B．③④C．②③D．②④
5．（2分）如图所示，两名举重运动员，乙比甲高，如果他们同时将相同质量的杠铃从地面匀速举过头顶，若甲比乙先完成，则下列判断正确的是（ ）
A．甲、乙运动员做功一样多
B．甲运动员做功较少，但功率较大
C．乙运动员做功较少，且功率较小
D．乙运动员做功较多
6．（2分）自行车沿斜坡匀速驶下的过程中，它具有的（ ）
A．重力势能减小，动能不变
B．重力势能减小，机械能不变
C．重力势能减小，动能增大
D．动能不变，机械能增大
7．（2分）将10ml的水与10ml的酒精相混合，混合后水和酒精的总体积小于20ml，这表明（ ）
A．分子之间存在着相互作用的引力
B．分子之间存在着相互作用的斥力
C．分子之间有空隙
D．分子是在不停地做无规则运动的
8．（2分）关于温度、内能和热量，下列说法中错误的是（ ）
A．同一物体，温度升高的越多，吸收的热量就越多
B．温度相同的两个物体间不会发生热传递
C．物体温度升高，一定需要吸收热量
D．任何物体都具有内能
9．（2分）密度公式为ρ＝，下面说法中正确的是（ ）
A．质量越大，物质的密度越大
B．体积越大，物质的密度越小
C．密度与物体的质量成正比、与体积成反比
D．密度可以用质量与体积的比值计算
10．（2分）甲、乙两物体在拉力F甲、F乙的作用下（F甲＞F乙），沿竖直方向向上做匀速直线运动。若不计空气阻力，则下列判断中正确的是（ ）
A．甲的合力一定大于乙的合力
B．甲的速度一定大于乙的速度
C．甲的动能可能小于乙的动能
D．甲的重力可能小于乙的重力
11．（2分）如图是内燃机的某个冲程，下列各现象中与该冲程能量的转化方式一致的是（ ）
A．滚摆上升B．火箭升空
C．钻木取火D．山中瀑布
12．（2分）甲、乙两个物体吸收相同热量后，甲升高的温度更高，以下判断中一定正确的是（ ）
A．若m甲＝m乙，则c甲＜c乙
B．若m甲＝m乙，则c甲＞c乙
C．若m甲＞m乙，则c甲＝c乙
D．若m甲＜m乙，则c甲＞c乙
13．（2分）同一物体分别挂在同一杠杆的右端或左端时，另一端分别用力F1，F2竖直向下作用，使杠杆水平平衡，则F1：F2为（ ）
A．l1：L2B．：C．l2：l1D．：
14．（2分）甲、乙两个圆柱形固体放置于水平地面上，质量相等，现分别在它们的上方各自水平切去一段质量，使得剩余的体积大小相等，问图中哪一个组合一定能保证甲切去的质量Δm甲大于乙切去的质量Δm乙（ ）
A．B．
C．D．
15．（2分）如图所示，底面积不同的轻质圆柱形容器分别盛有甲、乙两种液体。若从两容器中分别抽出相同高度的液体后，剩余液体质量相等，则液体密度、原来液体质量关系是（ ）
A．ρ甲一定小于ρ乙，m甲一定大于m乙
B．ρ甲一定小于ρ乙，m甲一定小于m乙
C．ρ甲一定小于ρ乙，m甲可能等于m乙
D．ρ甲可能小于ρ乙，m甲可能等于m乙
二、填空题（共30分）
16．（3.75分）神舟13号载人飞船从太空返回大气层时，与大气产生剧烈摩擦，外表温度升得很高，这是通过 方式改变了飞船外壳的内能，外壳的内能将 ；在此过程中，飞船的重力势能将 。（后两空均选填“变小”、“不变”或“变大”）
17．（3.75分）我国许多城市中都建有大型绿地，绿地中的人工湖具有“吸热”功能，盛夏时能大大减弱周围地区的“热岛效应”，这是因为水的比热容较 （选填“大”或“小”）。质量为1千克的水在太阳的照射下，温度升高5℃，水吸收的热量为 焦。[水的比热容为4.2×103 （填单位）]
18．（3.75分）如图（a）所示，水沸腾后，盖在试管口上的塞子会受到水蒸气的压力而冲出，此过程中，水蒸气的内能转化为塞子的 能，图（b）所示为四冲程汽油机的 冲程，这一冲程其能量转化情况与图5（a）中情况 （选填“相同”或“不同”）。
19．（3.75分）可燃冰有极强的燃烧力，1米3的可燃冰在常温常压下可释放164米3的天然气和产生0.8米3的淡水。已知可燃冰的密度为0.9克/厘米3，它表示的意义是：体积为1厘米3的可燃冰 为0.9克，则1.8千克的可燃冰体积为 米3，常温常压下可产生质量为 千克的淡水。
20．（3.75分）如图所示，某小组同学在塑料小桶中，分别装满密度已知的四种不同液体，用弹簧测力计依次测出它们的重力，记录数据如表所示。
①当小桶中盛满密度未知的某种液体时，弹簧测力计的示数为2.4牛。根据表中数据分析可知，此液体的密度为 克/厘米3。
②若把弹簧测力计和小桶改装为液体密度秤，该秤的“0刻度”线对应弹簧测力计上的刻度值为 牛。若要增大该称的称量范围，可换用以下两种规格的塑料小桶，符合要求的是 。（填写序号）
A．容积相同，质量更小的小桶 B．质量相同，容积更小的小桶。
21．（3.75分）如图所示，提升物体A的滑轮可以看作 杠杆。不计滑轮重及摩擦，物体A、B均重为20牛。当用力F2匀速提升物体B时，力F2大小为 牛。物体A、B移动的距离相等，F1与F2所做的功之比 。
22．（2.5分）如图所示，两个底面积不同的薄壁圆柱形容器内盛有体积相等的不同液体，密度分别为ρ甲、ρ乙。若从两容器内分别抽出相同深度的液体后，剩余液体的质量恰好相等，则ρ甲 ρ乙。如果抽出液体的质量分别为Δm甲、Δm乙，则Δm甲 Δm乙。（均选填“大于、“等于”或“小于”）
23．（2.5分）在两个相同的容器内分别装有甲、乙两种液体，液体的质量和比热容分别为m甲、c甲和m乙、c乙。当两液体分别吸收相同热量后，液体甲升高的温度较多。现将两容器中分别抽出相同质量的液体后，当剩余液体再次吸收相同热量时，发现液体乙升高的温度较多。由上述信息可知：m甲 m乙、c甲 c乙。（均选填“大于、“等于”或“小于”）
24．（2.5分）某同学发现冬天水管会“爆裂”，他通过查阅资料获得以下信息：（1）物体膨胀时如果遇到障碍，会产生很大的力；（2）金属会热胀冷缩；（3）水和冰在不同温度下的密度如表所示：
①根据表格中温度和密度的数据，得出结论：在1个标准大气压下，当0～4摄氏度时， 。
②指出水管“爆裂”的原因，并写出分析过程 。
三、综合题（共40分）
25．（4分）某同学设计了两种的独轮车，所对应的侧视图分别如图（a）、（b）所示。此同学最大提力为700牛。请问：
（1）该同学分别用两种独轮车运货物时，最多能装载的货物分别是多重？
（2）为了使图（b）中的独轮车能够装更重的货物，该同学能采取的措施是什么？并说明理由。
26．（6分）如图所示，薄壁圆柱形容器A、B的底面积分别为0.02米2和0.01米2，容器足够深。A、B两容器中分别装有0.15米高的水和2.4千克的酒精（ρ酒＝0.8×103千克/米3）。求：
（1）A容器中水的质量。
（2）B容器中酒精的深度。
（3）为了使A、B容器中液体的质量相等，小华、小芳、小林分别设计了不同的方法，如下表所示。请指出不可行的方法，再选择一位可行的，求出能使A、B容器中液体的质量相等时所要求的体积V0或高度h0。
27．（6分）如图所示，正方体甲是一个棱长0.4米的均匀正方体，质量为192千克，底面积为1×10﹣2米2、高为0.3米的薄壁轻质圆柱形容器乙放置于水平地面上，里面盛有0.2米深的水。
（1）求正方体甲的密度。
（2）若将甲竖切一块竖直放入乙容器中后沉底，被切部分的底面积为2×10﹣3米2，请通过计算判断水是否溢出。若溢出，求溢出水的质量；若不溢出，求此时水面的高度。
（3）若将甲竖切一块竖直放入乙容器中后沉底，水不溢出，求甲切下部分质量的最大值。
28．（8分）测定物质密度的实验原理是 。在“测定某金属密度”的实验中，首先用电子天平测得金属粒样本的质量为78克，然后在量筒中倒入20毫升的水后，将这些金属粒放入量筒中，现象如图所示，则这些金属粒的总体积为 厘米3，该金属的密度是 千克/米3。为了使测定的结果更精确，应该进行的操作是 。（选填“a”或“b”）
a.换用不同物质，多次测量。
b.改变金属粒数量，多次测量。
29．（10分）探究物质的吸热能力，通常有两种方案：
方案一：取相同质量的不同种物质，吸收相等的热量，比较温度的变化。
方案二：取相同质量的不同种物质，升高相同的温度，比较吸收的热量。
利用如图所示装置，小明和小红分别探究甲、乙、丙、丁四种液体的吸热能力，记录的实验数据如表一、表二。
表1：
表2：
①为了便于开展实验探究，在使用相同热源时，将方案中的“吸收的热量”进行了转换，通过测量 可知吸收热量的多少。
②分析表一中数据，可知小明同学采用 比较甲、乙两种液体的吸热能力（选填“方案一”或“方案二”）。
③分析表二中数据，可得出结论： 。由此说明 液体的吸热能力更强。
④若甲、乙、丙、丁四种液体均可作为发动机的冷却剂，则选用液体 作为冷却剂效果最佳（选填“甲”、“乙”、“丙”或“丁”）。
30．（6分）如图（a）所示为某课外小组自制的温度计，瓶子作为液泡装满某种液体，在密封的瓶塞上插上足够长的细管。为了探究薄壁细管内的液柱高度h与哪些因素有关，他们首先选用横截面积为S1的细管进行实验，把液泡浸没在不同温度的水中，如图（b）所示，并将数据记录在表一中。然后换用横截面积为S2的细管重复实验，将数据记录在表二中。（已知S1＞S2）
表一 横截面积S1
表二 横截面积S2
（1）分析比较实验序号 的数据及相关条件，可得出的初步结论是：同一液泡，t相同时，S越小，h越大。
（2）分析比较表一（或表二）中液柱高度h和温度t的数据及相关条件，可得出的初步结论是： 。
（3）接着该小组又进一步研究了表一（或表二）中液柱高度变化量Δh和温度变化量Δt的关系，可归纳得出的初步结论是： 。
2022-2023学年上海市上宝中学八年级（下）月考物理试卷
（5月份）
参考答案与试题解析
一、选择题（共30分）
1．（2分）已知空气密度为1.3千克/米3，你估算一下目前所在的教室中空气质量最接近（ ）
A．3千克B．30千克C．300千克D．3000千克
【分析】先估测出教室的长、宽、高，然后算出教室的容积，最后根据公式m＝ρV算出教室内空气的质量。
【解答】解：教室的长约为10m，宽约为5m，高约为4m，
则教室的容积：V＝长×宽×高＝10m×5m×4m＝200m3，
教室里空气的质量：m＝ρV＝1.3kg/m3×200m3＝260kg。
从选项中可以看出，选项C是正确的。
故选：C。
【点评】本题考查了密度公式的应用，能正确估测教室的长、宽、高是解答本题的关键。解答本题需要用密度公式去解决，不要凭空去猜测教室里空气的质量，否则很容易出错。
2．（2分）下列现象中，能说明分子在不停地做无规则运动的是（ ）
A．春天，落樱缤纷B．夏天，茉莉飘香
C．秋天，黄沙扑面D．冬天，雪花飘飘
【分析】不同物质互相接触时彼此进入对方的现象叫扩散，扩散现象说明了：一切物质的分子都在不停地做无规则运动。
【解答】解：由于分子的体积很小，分子的运动无法用肉眼直接看到，但可以通过气味、颜色的变化来体现。因此，落樱缤纷、黄沙扑面、雪花飘飘都不是扩散现象，是宏观物体的机械运动，不能说明分子在不停地做无规则运动，而茉莉飘香能说明分子在不停地做无规则运动。故ACD不符合题意，B符合题意。
故选：B。
【点评】分析现象时，注意分析是由物质的小颗粒形成的现象，还是由构成物质的微粒形成的现象，虽然现象相似，但形成现象的本质是很大不同的。
3．（2分）小明比较”测物质密度”和“探究物质质量与体积关系”两个实验后，认为：
①所测的物理量相同；
②测量的工具相同；
③多次测量的目的相同。
他的判断正确的是（ ）
A．①和②B．②和③C．①和③D．①、②和③
【分析】分析”测物质密度”和“探究物质质量与体积关系”两个实验需要测量的物理量以及使用的工具，分析清楚两次实验的目的，从而得出结论。
【解答】解：①在“测物质的密度”和“探究物质质量与体积的关系”两个实验中需测量的物理量都是：质量与体积，故①正确；
②在这两个实验中，都需用天平测出物体的质量，并用量筒根据排水法测出物体的体积，测量的工具相同，故②正确；
③探究物质质量与体积的关系是为了探究其规律性，应进行多次实验，所以，需要用不同体积的物体进行多次测量的目的是寻找普遍规律；
在“测定物质的密度”的实验中，为了减小实验误差，应进行多次实验，故两个实验中都需要进行多次测量，但多次测量的目的不同；故③错误；
综上分析可知A符合题意。
故选A。
【点评】本题考查”测物质密度”和“探究物质质量与体积关系”两个实验测量的物理量以及用到的测量工具，解题关键是分析清楚两次实验多次测量的目的。
4．（2分）下列各物理量可用来鉴别物质的是（ ）
①温度；
②密度；
③内能；
④比热容。
A．①②B．③④C．②③D．②④
【分析】物质的特性指的是这种物体特有的，可以用于区别其它物质的性质；密度、比热容都是物质的特性。
【解答】解：因为密度和比热容都是物质的特性，不同物质的密度和比热容一般是不同的，而温度和内能都不是物质的特性，和物质的种类没有关系，所以应该用密度和比热容来鉴别物质的种类。②④故正确，①③错误。
故选：D。
【点评】掌握密度是物质的特性，要想鉴别物质的种类，可以计算出它的密度，然后查密度表，看到底是那种物质，比热容也是物质的特性。
5．（2分）如图所示，两名举重运动员，乙比甲高，如果他们同时将相同质量的杠铃从地面匀速举过头顶，若甲比乙先完成，则下列判断正确的是（ ）
A．甲、乙运动员做功一样多
B．甲运动员做功较少，但功率较大
C．乙运动员做功较少，且功率较小
D．乙运动员做功较多
【分析】由题知甲比乙高，举起相同的杠铃时，举起的高度大，根据W＝Gh分析做功大小，又知道甲比乙先完成，再利用P＝比较功率大小。
【解答】解：两人举起的杠铃质量相同，则杠铃重相同，
乙比甲高，则举起的高度：h乙＞h甲，
由W＝Gh可知，举起杠铃做的功：W乙＞W甲，
若甲比乙先完成，则甲用时少，即t乙＞t甲，
根据P＝知，无法比较其功率大小。
由综上分析可知：选项D正确，ABC错误。
故选：D。
【点评】本题考查了学生对功的公式、功率的公式的掌握和运用，能分析出高个运动员举起的高度大是本题的突破口。
6．（2分）自行车沿斜坡匀速驶下的过程中，它具有的（ ）
A．重力势能减小，动能不变
B．重力势能减小，机械能不变
C．重力势能减小，动能增大
D．动能不变，机械能增大
【分析】自行车沿斜坡匀速驶下的过程中，没有发生弹性形变，不具有弹性势能，只考虑动能、重力势能、机械能。
（1）动能大小的影响因素：质量、速度。质量越大，速度越大，动能越大。
（2）重力势能大小的影响因素：质量、被举得高度。质量越大，高度越高，重力势能越大。
（3）机械能＝动能+势能。
【解答】解：自行车沿斜坡匀速驶下的过程中，质量不变，速度不变，动能不变。高度减小，重力势能减小。
自行车驶下过程中，没有发生弹性形变，不具有弹性势能，机械能＝动能+势能，动能不变，势能减小，机械能减小。
故选：A。
【点评】掌握动能、重力势能、弹性势能的影响因素。利用控制变量法，判断动能、重力势能、弹性势能、机械能的变化。
7．（2分）将10ml的水与10ml的酒精相混合，混合后水和酒精的总体积小于20ml，这表明（ ）
A．分子之间存在着相互作用的引力
B．分子之间存在着相互作用的斥力
C．分子之间有空隙
D．分子是在不停地做无规则运动的
【分析】根据分子的性质可以知道，分子之间有间隔，可以据此分析将10mL酒精和10mL 水混合在一起，体积小于20mL的原因。
【解答】解：分子之间有间隔，将10mL酒精和10mL水混合在一起后，水分子和酒精分子相互渗透对方的空隙之中，从而使混合后的总体积体积小于20mL。
故选：C。
【点评】要理解和熟记利用分子与原子的性质分析和解决问题的方法和技巧，以及分子与原子的概念和本质区别等相关的知识。
8．（2分）关于温度、内能和热量，下列说法中错误的是（ ）
A．同一物体，温度升高的越多，吸收的热量就越多
B．温度相同的两个物体间不会发生热传递
C．物体温度升高，一定需要吸收热量
D．任何物体都具有内能
【分析】（1）根据公式Q＝cmΔt可分析吸热多少与温度变化的关系；
（2）热传递发生的条件是有温度差；
（3）物体温度升高，可能是吸收了热量，也可能是外界对物体做了功；
（4）一切物体都具有内能。
【解答】解：A、由公式Q＝cmΔt可知，同一物体，比热容和质量相同，当升高温度多时，其吸收的热量就越多，故A正确；
B、热传递发生的条件是有温度差，温度相同的两个物体间不会发生热传递，故B正确；
C、物体温度升高，不一定需要吸收热量，也可能是外界对物体做了功，故C错误；
D、任何物体都具有内能，故D正确。
故选：C。
【点评】本题考查了对温度、内能和热量的概念以及它们之间关系的认识，属热学基础题。
9．（2分）密度公式为ρ＝，下面说法中正确的是（ ）
A．质量越大，物质的密度越大
B．体积越大，物质的密度越小
C．密度与物体的质量成正比、与体积成反比
D．密度可以用质量与体积的比值计算
【分析】密度是物质的特性，与质量和体积无关。根据密度公式可知，质量与密度和体积的关系，当质量相等时，体积越大，密度越小。质量与体积的比值越大，就表示物质的密度越大。
【解答】解：
ABC、密度是物质的特性，与质量和体积没有关系，ABC错误；
D、密度的定义为：质量与体积的比值。质量与体积的比值表示物质的密度，密度可以用质量与体积的比值计算，故D正确；
故选：D。
【点评】本题考查了对密度特性的理解，属于中档题。
10．（2分）甲、乙两物体在拉力F甲、F乙的作用下（F甲＞F乙），沿竖直方向向上做匀速直线运动。若不计空气阻力，则下列判断中正确的是（ ）
A．甲的合力一定大于乙的合力
B．甲的速度一定大于乙的速度
C．甲的动能可能小于乙的动能
D．甲的重力可能小于乙的重力
【分析】（1）平衡力合力为零；
（2）根据题意可知，甲乙做匀速直线运动，但无法确定速度的大小；
（3）根据二力平衡条件判断重力的大小，然后再比较动能的大小。
【解答】解：
A、甲乙都处于平衡状态，在竖直方向上受到的重力和拉力是一对平衡力，两者大小相等，合力都为零，故A错误；
B、甲、乙两物体在拉力F甲、F乙的作用下且F甲＞F乙，沿竖直方向向上做匀速直线运动，不能确定物体运动速度的大小，故B错误；
CD、甲乙都处于平衡状态，在竖直方向上受到的重力和拉力是一对平衡力，两者大小相等，因为F甲＞F乙，所以G甲＞G乙，故D错误；
由于物体运动的速度大小关系未知，、甲的速度可能小于乙的速度，所以甲的动能可能小于乙的动能，故C正确。
故选：C。
【点评】此题考查了二力平衡的条件的应用、动能大小的比较等知识点，是一道基础题，难度不大。
11．（2分）如图是内燃机的某个冲程，下列各现象中与该冲程能量的转化方式一致的是（ ）
A．滚摆上升B．火箭升空
C．钻木取火D．山中瀑布
【分析】内燃机是利用内能做功的机器，其在工作时有四个冲程，即吸气、压缩、做功、排气四个冲程。其中压缩冲程将机械能转化为内能；做功冲程将内能转化为机械能。由进气门和排气门的关闭和打开情况、活塞的上行和下行情况来判断是哪个冲程。然后分析四个选项中的能量转化，并找出与其相同的过程。
【解答】解：
由图可知，进气门和排气门都是关闭的，火花塞点火，活塞下行，因此是做功冲程，做功冲程中内能转化为机械能；
A、滚摆上升，质量不变，高度增加，重力势能增大，速度减小，动能减小，动能转化为重力势能，故A不合题意；
B、火箭升空时，将内能转化为机械能，故B符合题意；
C、钻木取火是克服摩擦做功，将机械能转化为内能，故C不合题意；
D、山中瀑布质量不变，高度减小，重力势能减少，速度增大，动能增加，重力势能转化为动能，故D不合题意。
故选：B。
【点评】此题要结合内燃机的四个冲程特点和冲程中的能量转化关系以及分析清楚不同场景中涉及的能量转化。
12．（2分）甲、乙两个物体吸收相同热量后，甲升高的温度更高，以下判断中一定正确的是（ ）
A．若m甲＝m乙，则c甲＜c乙
B．若m甲＝m乙，则c甲＞c乙
C．若m甲＞m乙，则c甲＝c乙
D．若m甲＜m乙，则c甲＞c乙
【分析】甲物体吸收的热量Q甲＝c甲m甲Δt甲，乙物体吸收的热量Q乙＝c乙m乙Δt乙，由题知，甲、乙两物体吸收相等的热量，可得c甲m甲Δt甲＝c乙m乙Δt乙，而甲物体的温度变化量大，可得c甲m甲＜c乙m乙，据此对每个选项的正误做出判断。
【解答】解：由热量的计算公式Q吸＝cmΔt可得：甲吸收的热量Q甲＝c甲m甲Δt甲，乙吸收的热量Q乙＝c乙m乙Δt乙，
由Q甲＝Q乙可知：c甲m甲Δt甲＝c乙m乙Δt乙，
由题意知：Δt甲＞Δt乙；故c甲m甲＜c乙m乙，
若m甲＝m乙，则c甲＜c乙；
若m甲＞m乙，则c甲＜c乙。
若m甲＜m乙，则c甲与c乙的大小关系无法判断。
故选：A。
【点评】本题考查了吸热公式Q甲＝cmΔt的应用，注意理解：在c甲m甲＜c乙m乙的情况下，若c甲＜c乙，则有3种可能，即m甲＝m乙、m甲＜m乙、m甲＞m乙。
13．（2分）同一物体分别挂在同一杠杆的右端或左端时，另一端分别用力F1，F2竖直向下作用，使杠杆水平平衡，则F1：F2为（ ）
A．l1：L2B．：C．l2：l1D．：
【分析】杠杆的平衡条件：动力×动力臂＝阻力×阻力臂，即通过F1×L1＝F2×L2；
根据杠杆的平衡条件即可求出力的比值。
【解答】解：根据杠杆的平衡条件：左图中，F1•l1＝G•l2；拉力F1＝；
右图中，G•l1＝F2•l2；拉力F2＝；
所以F1：F2＝：＝：。
故选：D。
【点评】本题考查杠杆的平衡条件，关键是公式的灵活运用，有一定的难度。
14．（2分）甲、乙两个圆柱形固体放置于水平地面上，质量相等，现分别在它们的上方各自水平切去一段质量，使得剩余的体积大小相等，问图中哪一个组合一定能保证甲切去的质量Δm甲大于乙切去的质量Δm乙（ ）
A．B．
C．D．
【分析】已知甲、乙两个圆柱形固体放置于水平地面上，质量相等，根据甲切去的质量Δm甲大于乙切去的质量Δm乙，剩余的体积大小相等，可推出甲、乙的密度关系，然后可知二者体积关系，由此可作出选择。
【解答】解：已知m甲＝m乙，当甲切去的质量Δm甲大于乙切去的质量Δm乙，
即m甲剩＜m乙剩，
又因为使得剩余的体积大小相等，即V甲剩＝V乙剩，
由ρ＝可知，剩余的甲、乙密度关系，即甲、乙的密度关系，ρ甲＜ρ乙，
已知m甲＝m乙，由ρ＝可知，
甲、乙两个圆柱形原来的体积V甲＞V乙，则只有A符合。
故选：A。
【点评】此题考查密度公式及其变形的应用，根据已知条件判断出ρ甲＜ρ乙，是解答此题的关键。
15．（2分）如图所示，底面积不同的轻质圆柱形容器分别盛有甲、乙两种液体。若从两容器中分别抽出相同高度的液体后，剩余液体质量相等，则液体密度、原来液体质量关系是（ ）
A．ρ甲一定小于ρ乙，m甲一定大于m乙
B．ρ甲一定小于ρ乙，m甲一定小于m乙
C．ρ甲一定小于ρ乙，m甲可能等于m乙
D．ρ甲可能小于ρ乙，m甲可能等于m乙
【分析】（1）由图可知，甲液体的高度大于乙液体的高度，即h甲＞h乙，从两容器中分别抽出相同高度的液体后，剩余的甲液体高度仍然大于乙剩余液体的高度；由图可知，甲容器的底面积大于乙容器的底面积，则甲剩余液体的体积大于乙剩余液体的体积，而剩余液体质量相等，则根据ρ＝可判断甲、乙液体密度的大小关系；
（2）从两容器中分别抽出相同高度的液体，则甲抽出的液体的体积大于乙抽出液体的体积，由于甲液体的密度小于乙液体的密度，根据密度公式分析甲、乙抽出液体的质量关系，据此判断原来液体的质量关系。
【解答】解：由图可知，甲液体的高度大于乙液体的高度，即h甲＞h乙，从两容器中分别抽出相同高度的液体后，剩余的甲液体高度仍然大于乙剩余液体的高度，即h甲′＞h乙′，
甲的底面积大于乙的底面积，即S甲＞S乙，则甲剩余液体的体积大于乙剩余液体的体积，
根据题意可知，剩余液体质量相等，由ρ＝可知，甲液体的密度小于乙液体的密度，即ρ甲一定小于ρ乙；
从两容器中分别抽出相同高度的液体，则甲抽出的液体的体积大于乙抽出液体的体积，由于甲液体的密度小于乙液体的密度，
由ρ＝的变形公式m＝ρV可知，甲抽出液体的质量可能大于乙抽出液体的质量、也可能等于乙抽出液体的质量、也可能小于乙抽出液体的质量，
所以原来甲液体的质量可能大于乙液体的质量，也可能等于乙液体的质量，也可能小于乙液体的质量，即m甲可能大于m乙、可能等于m乙、也可能小于m乙，故ABD错误、C正确。
故选：C。
【点评】本题考查密度公式的应用，难点在于判断液体体积的关系。
二、填空题（共30分）
16．（3.75分）神舟13号载人飞船从太空返回大气层时，与大气产生剧烈摩擦，外表温度升得很高，这是通过 做功 方式改变了飞船外壳的内能，外壳的内能将 变大 ；在此过程中，飞船的重力势能将 变小 。（后两空均选填“变小”、“不变”或“变大”）
【分析】改变内能的方式包括做功和热传递；
重力势能大小的影响因素：物体的质量、物体的高度。
【解答】解：飞船从太空返回大气层时，与大气层之间摩擦做功，内能增加，温度升高，通过做功的方式改变飞船外壳的内能；
在此过程中，高度减小，质量不变，重力势能减小。
故答案为：做功；变大；变小。
【点评】本题考查内能的改变和机械能的变化，属于基础题。
17．（3.75分）我国许多城市中都建有大型绿地，绿地中的人工湖具有“吸热”功能，盛夏时能大大减弱周围地区的“热岛效应”，这是因为水的比热容较 大 （选填“大”或“小”）。质量为1千克的水在太阳的照射下，温度升高5℃，水吸收的热量为 2.1×104 焦。[水的比热容为4.2×103 J/（kg•℃） （填单位）]
【分析】水的比热容较大，相同质量的水和其它物质比较，吸收或放出相同的热量，水的温度升高或降低的少。
根据公式Q＝cmΔt，可计算1千克水温度升高5℃吸收的热量。
【解答】解：水的比热容较大，相同质量的水和土壤、砂石比较，吸收或放出相同的热量，水的温度升高或降低的少，所以盛夏时能大大减弱周围地区的“热岛效应”；
水的比热容是4.2×103J/（kg•℃），质量为1千克的水在太阳的照射下，温度升高5℃，水吸收的热量为：Q＝cmΔt＝4.2×103J/（kg•℃）×1kg×5℃＝2.1×104J。
故答案为：大；2.1×104；J/（kg•℃）。
【点评】本题考查了利用水的比热容大的特性，来解释生活中的现象，同时考查了对吸热公式的运用，属热学基础题。
18．（3.75分）如图（a）所示，水沸腾后，盖在试管口上的塞子会受到水蒸气的压力而冲出，此过程中，水蒸气的内能转化为塞子的 机械 能，图（b）所示为四冲程汽油机的 压缩 冲程，这一冲程其能量转化情况与图5（a）中情况 不同 （选填“相同”或“不同”）。
【分析】（1）做功改变内能的实质是能量的转化，对物体做功是内能转化为机械能；橡皮塞冲出过程也是水蒸气的内能转化为塞子机械能的过程，水蒸气的内能会减小，温度降低；在内燃机的做功冲程中，能量转化关系是内能转化为机械能；
（2）根据活塞的运行方向和气门的关闭情况判断是哪一个冲程；内燃机的压缩冲程是活塞压缩气缸内气体做功，机械能转化为内能；
【解答】解：（1）图a中，水吸热迅速的汽化，形成大量的水蒸气，水蒸气对塞子做功，将水蒸气的内能转化为木塞的机械能。
四冲程汽油机工作过程中的做功冲程与上述能量转化过程相同；
（2）图b中，活塞上行，气门关闭，所以是压缩冲程；
在汽油机的压缩冲程中，压缩气体时对气体做功，气体的内能增大，气体的温度升高，是机械能转化为内能；这一能量转化与图a中情况不同。
故答案为：机械；压缩；不同。
【点评】本题考查的是能量的转化、热传递和做功改变物体的内能、内燃机的四个冲程等知识，是一道基础题，比较简单。
19．（3.75分）可燃冰有极强的燃烧力，1米3的可燃冰在常温常压下可释放164米3的天然气和产生0.8米3的淡水。已知可燃冰的密度为0.9克/厘米3，它表示的意义是：体积为1厘米3的可燃冰 质量 为0.9克，则1.8千克的可燃冰体积为 2×10﹣3 米3，常温常压下可产生质量为 1.6 千克的淡水。
【分析】（1）密度单位：1g/cm3＝1×103kg/m3，知道可燃冰的质量，利用ρ＝求可燃冰的体积；
（2）由题知，1m3的可燃冰在常温常压下可产生0.8m3的淡水，可求2×10﹣3m3可燃冰在常温常压下产生的淡水的体积，再利用m＝ρV求其质量。
【解答】解：
（1）可燃冰的密度：ρ可燃冰＝0.9g/cm3＝0.9×103kg/m3，它表示的意义是：体积为1厘米3的可燃冰质量为0.9克，
由ρ＝可得，1.8千克的可燃冰体积：
V可燃冰＝＝＝2×10﹣3m3；
（2）由题知，1m3的可燃冰在常温常压下可产生0.8m3的淡水，
则2×10﹣3m3可燃冰在常温常压下产生淡水的体积：
V水＝2×10﹣3m3×0.8＝1.6×10﹣3m3，
由ρ＝得产生淡水的质量：
m水＝ρ水V水＝1×103kg/m3×1.6×10﹣3m3＝1.6kg。
故答案为：质量；2×10﹣3；1.6。
【点评】本题考查了密度公式的应用，计算时注意单位换算：1g/cm3＝1×103kg/m3。
20．（3.75分）如图所示，某小组同学在塑料小桶中，分别装满密度已知的四种不同液体，用弹簧测力计依次测出它们的重力，记录数据如表所示。
①当小桶中盛满密度未知的某种液体时，弹簧测力计的示数为2.4牛。根据表中数据分析可知，此液体的密度为 1.6 克/厘米3。
②若把弹簧测力计和小桶改装为液体密度秤，该秤的“0刻度”线对应弹簧测力计上的刻度值为 0.8 牛。若要增大该称的称量范围，可换用以下两种规格的塑料小桶，符合要求的是 A、B 。（填写序号）
A．容积相同，质量更小的小桶 B．质量相同，容积更小的小桶。
【分析】（1）分析表格知，每组弹簧测力计的示数和液体密度在数值上都相差0.8，可通过这一规律总结出它们的函数关系，ρ＝F﹣0.8，所以将2.4N代入即可求出该液体的密度；
（2）由函数关系可知，零刻度ρ＝0g/cm3时，F＝0.8N；
由于液体密度秤是由测力计改成的；知道测力计的拉力量程是不变的；
若要增大液体密度秤的密度称量范围，根据测力计的最大拉力是不变的，利用F＝G+G桶求出ρ液＝；然后分析判断即可。
【解答】解：（1）根据表中数据总结出的函数关系ρ＝F﹣0.8，将F＝2.4N代入得ρ＝2.4﹣0.8＝1.6g/cm3；
（2）该秤的“0刻度”线时，即ρ＝0，由于函数关系ρ＝F﹣0.8可得：F＝0+0.8＝0.8，即弹簧测力计的示数为0.8N；
把弹簧测力计和小桶改装为液体密度秤，则测力计的最大拉力F＝G+G桶，即：F＝mg+m桶g＝ρ液V容积g，
所以：ρ液＝；
由于液体密度秤是由测力计改成的；测力计的最大拉力F是不变的；
若利用容积相同，质量更小的小桶，则在相同体积的液体，液体的质量变大时，密度也变大；
若利用质量相同的小桶，液体的密度与容积成反比。
故AB都符合要求。
故答案为：①1.6；②0.8；A、B。
【点评】本题考查测力计的原理和应用，能根据图表探究物质的规律是近两年出现较多的题目，图象可以使我们建立更多的感性认识，从表象中去探究本质规律，体验知识的形成过程；本题的难点是测力计的最大拉力是不变的。
21．（3.75分）如图所示，提升物体A的滑轮可以看作 等臂 杠杆。不计滑轮重及摩擦，物体A、B均重为20牛。当用力F2匀速提升物体B时，力F2大小为 10 牛。物体A、B移动的距离相等，F1与F2所做的功之比 1：1 。
【分析】定滑轮使用时，滑轮的位置固定不变；定滑轮实质是等臂杠杆，不省力也不费力，但可以改变作用力方向；
动滑轮使用时，滑轮随物体移动；动滑轮实质是一个动力臂为阻力臂两倍的杠杆，能省一半力，但不能改变力的方向；
功的原理：使用任何机械都不省功。
【解答】解：由图知提升物体A的滑轮是定滑轮，可以看作等臂杠杆；
提升物体B的滑轮是动滑轮，能省力一半，不计滑轮重及摩擦，当用力F2匀速提升物体B时，力F2＝G＝×20N＝10N；
不计滑轮重及摩擦，由功的原理知，物体A、B移动的距离相等，F1与F2所做的功W1＝W2＝Gh，即F1与F2所做的功之比为1：1。
故答案为：等臂；10；1：1。
【点评】本题考查对定滑轮和动滑轮的认识，以及功的原理的应用，属于一道基础题。
22．（2.5分）如图所示，两个底面积不同的薄壁圆柱形容器内盛有体积相等的不同液体，密度分别为ρ甲、ρ乙。若从两容器内分别抽出相同深度的液体后，剩余液体的质量恰好相等，则ρ甲 大于 ρ乙。如果抽出液体的质量分别为Δm甲、Δm乙，则Δm甲 大于 Δm乙。（均选填“大于、“等于”或“小于”）
【分析】（1）首先根据图示判断容器内两种液体的体积关系，然后根据密度公式判断两种液体的密度关系；
（2）两容器内液体质量相等，根据图示，通过比较在两容器中分别再抽掉相同深度的原液体两种液体的总质量，判断抽掉的质量Δm甲与Δm乙的关系。
【解答】解：（1）由图知，甲容器的底面积大于乙容器的底面积，乙液体的体积等于甲液体的体积，V甲＝V乙，
若从两容器内分别抽出相同深度的液体，则V甲抽＞V乙抽，剩余液体的体积，V甲剩＜V乙剩，
又知剩余液体的质量恰好相等，根据密度公式知，ρ甲＞ρ乙；
（2）由于V甲抽＞V乙抽，ρ甲＞ρ乙，根据密度公式的变形式m＝ρV得，抽出液体的质量Δm甲＞Δm乙。
故答案为：大于；大于。
【点评】此题考查密度公式及其应用，关键是通过图示得出两种液体的密度关系，中档题。
23．（2.5分）在两个相同的容器内分别装有甲、乙两种液体，液体的质量和比热容分别为m甲、c甲和m乙、c乙。当两液体分别吸收相同热量后，液体甲升高的温度较多。现将两容器中分别抽出相同质量的液体后，当剩余液体再次吸收相同热量时，发现液体乙升高的温度较多。由上述信息可知：m甲 大于 m乙、c甲 小于 c乙。（均选填“大于、“等于”或“小于”）
【分析】两液体分别吸收相同热量后，液体甲升高的温度较多，根据吸热公式得到c甲m甲＜c乙m乙，当剩余液体再次吸收相同热量时，发现液体乙升高的温度较多由吸热公式得到c甲m甲+c乙Δm＞c乙m乙+c甲Δm甲，进而推导出甲和乙的质量和比热容之间的关系。
【解答】解：由两液体分别吸收相同热量后，可知：c甲m甲Δt甲＝c乙m乙Δt乙，
由Δt甲＞Δt乙，可知c甲m甲＜c乙m乙，
将两容器中分别抽出相同质量的液体后，
当剩余液体再次吸收相同热量时，可知：c甲（m甲﹣Δm）Δt'甲＝c乙（m乙﹣Δm）Δt'乙，
由Δt甲＜Δt乙，
所以c甲（m甲﹣Δm）＞c乙（m乙﹣Δm），
即c甲m甲﹣c甲Δm＞c乙m乙﹣c乙Δm，
c甲m甲+c乙Δm＞c乙m乙+c甲Δm甲，
由于c甲m甲＜c乙m乙，
故c甲Δm＜c乙Δm，即c甲＜c乙，
由于c甲m甲＜c乙m乙，故m甲＞m乙。
故答案为：大于；小于。
【点评】本题考查了密度公式的应用，热量的计算等，难易程度适中，其中（3）题的关键是得出剩余液体的质量关系。
24．（2.5分）某同学发现冬天水管会“爆裂”，他通过查阅资料获得以下信息：（1）物体膨胀时如果遇到障碍，会产生很大的力；（2）金属会热胀冷缩；（3）水和冰在不同温度下的密度如表所示：
①根据表格中温度和密度的数据，得出结论：在1个标准大气压下，当0～4摄氏度时， 温度越低，水的密度越小 。
②指出水管“爆裂”的原因，并写出分析过程 冬天温度降低，水会结成冰，体积增大；加上金属（水管）热胀冷缩，体积变小，管内的冰（水）膨胀时，遇到障碍，产生很大的力，撑爆水管 。
【分析】根据表格数据可以分析出温度和水的关系；水变成冰，体积变大，金属受冷会收缩，从而产生比较大的力。
【解答】解：①由表格可知，当0～4摄氏度时，温度降低，密度在变小；
②冬天温度降低，水会结成冰，体积增大；加上金属（水管）热胀冷缩，体积变小，管内的冰（水）膨胀时，遇到障碍，产生很大的力，撑爆水管。
故答案为：①温度越低，水的密度越小；
②冬天温度降低，水会结成冰，体积增大；加上金属（水管）热胀冷缩，体积变小，管内的冰（水）膨胀时，遇到障碍，产生很大的力，撑爆水管。
【点评】本题考查了密度的实际应用，有一定难度。
三、综合题（共40分）
25．（4分）某同学设计了两种的独轮车，所对应的侧视图分别如图（a）、（b）所示。此同学最大提力为700牛。请问：
（1）该同学分别用两种独轮车运货物时，最多能装载的货物分别是多重？
（2）为了使图（b）中的独轮车能够装更重的货物，该同学能采取的措施是什么？并说明理由。
【分析】（1）图中给出了力臂大小，已知力臂和所用力，利用杠杆平衡条件可求得使用各种独轮车运货物的重力。
（2）根据杠杆的平衡条件，当在动力和动力臂不变时一定时，阻力臂越小，阻力越大分析解答。
【解答】解：（1）图a动力臂为L1＝60cm，阻力臂L2＝60cm+90cm＝150cm，F1＝700N，
由杠杆平衡条件可得F1L1＝F2L2，
即700N×60cm＝F2×150cm，
G＝F2＝280N；
图b动力臂为L1＝60cm+90cm＝150cm，阻力臂L2＝60cm，F1＝700N，
由杠杆平衡条件可得F1L1＝F2L2，
即700N×150cm＝F2×60cm，
G'＝F2＝1750N；
（2）为了使图（b）中的独轮车能够装更重的货物，根据杠杆平衡条件可知，在动力和动力臂不变时，可以减小阻力臂，即将物体向支点靠拢，就可以增大阻力，能够装更重的货物。
答：（1）该同学分别用两种独轮车运货物时，最多能装载的货物分别是280N、1750N；
（2）为了使图（b）中的独轮车能够装更重的货物，采取的措施是将物体向支点靠近轮子，理由是减小阻力臂。
【点评】本题考查杠杆平衡条件的应用，属于中档题。
26．（6分）如图所示，薄壁圆柱形容器A、B的底面积分别为0.02米2和0.01米2，容器足够深。A、B两容器中分别装有0.15米高的水和2.4千克的酒精（ρ酒＝0.8×103千克/米3）。求：
（1）A容器中水的质量。
（2）B容器中酒精的深度。
（3）为了使A、B容器中液体的质量相等，小华、小芳、小林分别设计了不同的方法，如下表所示。请指出不可行的方法，再选择一位可行的，求出能使A、B容器中液体的质量相等时所要求的体积V0或高度h0。
【分析】（1）由容器A的底面积和容器A中水的深度，可求出水的体积，再由密度公式即可求出容器A中水的质量；
（2）已知容器B中酒精的质量和酒精密度，由密度公式可求出酒精的体积，已知容器B底面积，再由圆柱体体积公式，可求出酒精的深度；
（3）通过计算可知酒精体积和水的体积关系，也可知二者质量关系，即能选出不可行的方案。
【解答】解：（1）容器A中水的体积V水＝SAh水＝0.02m2×0.15m＝0.003m3，
容器A中水的质量m水＝ρ水V水＝1.0×103kg/m3×0.003m3＝3kg；
（2）容器B中酒精的体积V酒＝＝＝3×10﹣3m3，
容器B酒精的深度h酒＝＝＝0.3m；
（3）m水＞m酒，若使A、B容器中液体的质量相等，可行的是小华和小林的方案，不可行的为小芳的方案；
若选择小华的方案：m水﹣ρ水V0＝m酒+ρ酒V0，即3kg﹣1.0×103kg/m3×V0＝2.4kg+0.8×103kg/m3×V0；
解得V0＝m3≈3.33×10﹣4m3；
若选择小芳的方案：m水﹣ρ水V0＝m酒﹣ρ酒V0，即3kg﹣1.0×103kg/m3×V0＝2.4kg﹣0.8×103kg/m3×V0；
解得V0＝0.003m3，又V水＝V酒＝0.003m3，故在A容器中抽出体积V0的水，在B容器中抽出体积V0的酒精，此时容器为空的，所以不可行。
若选择小林的方案：在A容器中抽出高度h0的水，则抽出水的体积V水′＝SAh0；在B容器中抽出高度h0的酒精，则抽出酒精的体积V酒′＝SBh0；
由题意得：m水﹣ρ水V水′＝m酒﹣ρ水V酒′，即m水﹣ρ水SAh0＝m酒﹣ρ酒SBh0；
代入数值：3kg﹣1.0×103kg/m3×0.02m2×h0＝2.4kg﹣0.8×103kg/m3×0.01m2×h0，
解得h0＝0.05m。
答：（1）A容器中水的质量3kg；
（2）B容器中酒精的深度0.3m；
（3）使A、B容器中液体的质量相等时，小芳的方案不可行；若选小华的方案，V0≈3.33×10﹣4m3；若选小林的方案，h0＝0.05m。
【点评】本题考查密度的计算和公式应用，前两问比较基础，第三问应用的数学的等式，中考题出的可能性不大。
27．（6分）如图所示，正方体甲是一个棱长0.4米的均匀正方体，质量为192千克，底面积为1×10﹣2米2、高为0.3米的薄壁轻质圆柱形容器乙放置于水平地面上，里面盛有0.2米深的水。
（1）求正方体甲的密度。
（2）若将甲竖切一块竖直放入乙容器中后沉底，被切部分的底面积为2×10﹣3米2，请通过计算判断水是否溢出。若溢出，求溢出水的质量；若不溢出，求此时水面的高度。
（3）若将甲竖切一块竖直放入乙容器中后沉底，水不溢出，求甲切下部分质量的最大值。
【分析】（1）先根据正方体体积公式算出体积，再由密度公式求出甲的密度；
（2）根据被切部分的底面积和棱长可算出切去部分的体积，即放入乙容器中物体的体积；根据圆柱形容器乙底面积和高，可计算容器乙的容积；再由里面水的高，可计算出容器乙中水的体积；用容器乙的容积减掉容器乙中水的体积，可算出容器乙空的部分体积，后与放入乙容器中物体的体积比较，若前者大，水不溢出，若前者小，水溢出。
（3）若将甲竖切一块竖直放入乙容器中后沉底，水若刚好达到容器乙口，则甲切下部分质量的最大。
【解答】解：（1）V＝（0.4m）3＝0.064m3，＝＝3×103kg/m3；
（2）切去部分的体积V切＝2×10﹣3m2×0.4m＝8×10﹣4m3，即放入乙容器中物体的体积为8×10﹣4m3，
容器乙的容积V容＝1×10﹣2m2×0.3m＝3×10﹣3m3，容器乙中水的体积V水＝1×10﹣2m2×0.2m＝2×10﹣3m3，容器乙空部分体积V空＝V容﹣V水＝1×10﹣3m3；
所以V空＞V切，故水不会溢出；
（3）将甲切掉部分放入容器乙中，若水刚好不溢出时，切下质量最大，
即V切′＝V空＝1×10﹣3m3，由得m切max＝ρ•V切′＝3×103kg/m3×1×10﹣3m3＝3kg。
答：（1）正方体甲的密度3×103kg/m3；
（2）水不会溢出；
（3）甲切下部分质量的最大值为3kg。
【点评】本题考查密度的计算，注重理解能力的培养。
28．（8分）测定物质密度的实验原理是 ρ＝ 。在“测定某金属密度”的实验中，首先用电子天平测得金属粒样本的质量为78克，然后在量筒中倒入20毫升的水后，将这些金属粒放入量筒中，现象如图所示，则这些金属粒的总体积为 10 厘米3，该金属的密度是 7.8×103 千克/米3。为了使测定的结果更精确，应该进行的操作是 b 。（选填“a”或“b”）
a.换用不同物质，多次测量。
b.改变金属粒数量，多次测量。
【分析】（1）求出物体的质量和体积，根据密度公式ρ＝即可求出物体的密度；
（2）金属粒样本的体积体积为量筒两次体积读数之差，密度用ρ＝计算；
（3）多次测量求平均值减小误差。
【解答】解：（1）测量密度的实验原理为ρ＝；
（2）图中金属粒和水的总体积为30mL，
金属粒的体积为V＝30mL﹣20mL＝10mL＝10cm3，
金属粒的密度：ρ＝＝＝7.8g/cm3＝7.8×103kg/m3；
（3）多次测量求平均值可以减小误差，使测定的结果更精确，所以实验中需要改变金属粒数量，多次测量，故选：b。
故答案为：ρ＝；10；7.8×103；b。
【点评】本题考查了测量物体密度的原理、量筒的读数、密度的计算、多测测量的密度以及与要探究物质质量与体积的关系的相同点和不同点等知识，是一道综合题，但难度不大。
29．（10分）探究物质的吸热能力，通常有两种方案：
方案一：取相同质量的不同种物质，吸收相等的热量，比较温度的变化。
方案二：取相同质量的不同种物质，升高相同的温度，比较吸收的热量。
利用如图所示装置，小明和小红分别探究甲、乙、丙、丁四种液体的吸热能力，记录的实验数据如表一、表二。
表1：
表2：
①为了便于开展实验探究，在使用相同热源时，将方案中的“吸收的热量”进行了转换，通过测量 加热时间长短 可知吸收热量的多少。
②分析表一中数据，可知小明同学采用 方案二 比较甲、乙两种液体的吸热能力（选填“方案一”或“方案二”）。
③分析表二中数据，可得出结论： 相同质量的两种液体，加热相同时间，吸收相同的热量，温度变化小的物质，吸热能力强 。由此说明 丙 液体的吸热能力更强。
④若甲、乙、丙、丁四种液体均可作为发动机的冷却剂，则选用液体 甲 作为冷却剂效果最佳（选填“甲”、“乙”、“丙”或“丁”）。
【分析】（1）我们使用相同的酒精灯（或加热器）通过加热时间的长短来比较吸热多少，这种方法叫转换法；
（2）①②比较物质吸热能力的2种方法：
使相同质量的不同物质升高相同的温度，比较吸收的热量（即比较加热时间），吸收热量多的吸热能力强；
使相同质量的不同物质吸收相同的热量（即加热相同的时间），比较温度的变化，温度变化小的吸热能力强。
【解答】解：（1）实验中使用相同的酒精灯对其进行加热，根据转换法，通过加热时间长短可知吸收热量的多少；
（2）分析表一中信息，升高相同的温度，比较加热时间的长短，故小明采用的是方案二；
（3）分析表二中数据，相同质量的丙、丁两种液体，加热相同时间，吸收相同的热量，丙的温度变化小，则丙的吸热能力强；
（4）对比表1数据可知，相同质量的甲、乙两种液体，升高相同的温度，甲所需时间长，吸收热量多，则甲的吸热能力强，
分析表二中数据，加热相同时间，吸收相同的热量，丙的温度变化小，则丙的吸热能力强，
对比甲、丙温度升高相同，甲需要加热时间4分钟，丙需要加热时间2分钟，故甲的吸热能力最强，甲的比热容最大，所以如果在甲、乙、丙、丁四种液体中选择一种作为冷却剂，应选甲液体更加合适。
故答案为：①加热时间长短；②方案二；③相同质量的两种液体，加热相同时间，吸收相同的热量，温度变化小的物质，吸热能力强；丙；④甲。
【点评】本题比较不同物质的吸热能力，考查控制变量法、转换法的应用和比较吸热能力的方法以及比热容大的运用，为热学中的重要实验。
30．（6分）如图（a）所示为某课外小组自制的温度计，瓶子作为液泡装满某种液体，在密封的瓶塞上插上足够长的细管。为了探究薄壁细管内的液柱高度h与哪些因素有关，他们首先选用横截面积为S1的细管进行实验，把液泡浸没在不同温度的水中，如图（b）所示，并将数据记录在表一中。然后换用横截面积为S2的细管重复实验，将数据记录在表二中。（已知S1＞S2）
表一 横截面积S1
表二 横截面积S2
（1）分析比较实验序号 3和9（或4和10） 的数据及相关条件，可得出的初步结论是：同一液泡，t相同时，S越小，h越大。
（2）分析比较表一（或表二）中液柱高度h和温度t的数据及相关条件，可得出的初步结论是： 同一液泡，细管横截面积S相同时，温度t越大，液柱高度h越大 。
（3）接着该小组又进一步研究了表一（或表二）中液柱高度变化量Δh和温度变化量Δt的关系，可归纳得出的初步结论是： 同一液泡，细管横截面积S相同时，温度变化量Δt越大，液柱高度变化量Δh越大 。
【分析】（1）根据控制变量法，要比较细管横截面积S和液柱高度h的关系，就要控制其他的变量相同，即控制液泡和温度t相同，改变细管横截面积S，观察液柱高度h的变化，据此分析解答；
（2）比较表一（或表二）中液柱高度h和温度t的数据，根据控制变量法分析解答；
（3）研究了表一（或表二）中液柱高度变化量Δh和温度变化量Δt的关系，根据控制变量法分析解答。
【解答】解：（1）根据控制变量法，要比较细管横截面积S和液柱高度h的关系，就要控制其他的变量相同，即控制液泡和温度t相同，改变细管横截面积S，观察液柱高度h的变化，所以分析比较实验序号3和9（或4和10）的数据及相关条件，可得出的初步结论是：同一液泡，t相同时，S越小，h越大；
（2）根据控制变量法，分析比较表一（或表二）中液柱高度h和温度t的数据及相关条件，可得出的初步结论是：同一液泡，细管横截面积S相同时，温度t越大，液柱高度h越大；
（3）根据控制变量法，研究了表一（或表二）中液柱高度变化量Δh和温度变化量Δt的关系，可归纳得到结论：同一液泡，细管横截面积S相同时，温度变化量Δt越大，液柱高度变化量Δh越大。
故答案为：（1）3和9（或4和10）；（2）同一液泡，细管横截面积S相同时，温度t越大，液柱高度h越大；（3）同一液泡，细管横截面积S相同时，温度变化量Δt越大，液柱高度变化量Δh越大。
【点评】本实验探究自制的温度计中薄壁细管内的液柱高度h与哪些因素有关，能结合表格中的数据得出结论是解决该题的关键。液体密度（克/厘米3）
0.6
0.8
1.0
1.2
弹簧测力计（牛）
1.4
1.6
1.8
2.0
形态
水
冰
温度（℃）
4
3
2
1
0
0
密度（克/厘米3）
0.9998
0.9996
0.9994
0.9991
0.9990
0.9101
同学
所设计的方法
小华
在A容器中抽出体积V0的水，在B容器中倒入体积V0的酒精
小芳
在A容器中抽出体积V0的水，在B容器中抽出体积V0的酒精
小林
在A容器中抽出高度h0的水，在B容器中抽出高度h0的酒精
液体名称
液体质量（克）
液体初温（℃）
液体末温（℃）
加热时间（分钟）
吸收的热量
小明
甲
5
20
30
4
多
乙
5
20
30
2
少
液体名称
液体质量（克）
液体初温（℃）
液体末温（℃）
加热时间（分钟）
吸收的热量
小红
丙
5
10
20
2
相同
丁
5
10
25
2
相同
实验序号
温度t（℃）
液柱高度h（cm）
1
0
5
2
10
7
3
30
11
4
60
17
5
100
25
实验序号
温度t（℃）
液柱高度h（cm）
6
0
6
7
5
7.5
8
15
10.5
9
30
15
10
60
24
液体密度（克/厘米3）
0.6
0.8
1.0
1.2
弹簧测力计（牛）
1.4
1.6
1.8
2.0
形态
水
冰
温度（℃）
4
3
2
1
0
0
密度（克/厘米3）
0.9998
0.9996
0.9994
0.9991
0.9990
0.9101
同学
所设计的方法
小华
在A容器中抽出体积V0的水，在B容器中倒入体积V0的酒精
小芳
在A容器中抽出体积V0的水，在B容器中抽出体积V0的酒精
小林
在A容器中抽出高度h0的水，在B容器中抽出高度h0的酒精
液体名称
液体质量（克）
液体初温（℃）
液体末温（℃）
加热时间（分钟）
吸收的热量
小明
甲
5
20
30
4
多
乙
5
20
30
2
少
液体名称
液体质量（克）
液体初温（℃）
液体末温（℃）
加热时间（分钟）
吸收的热量
小红
丙
5
10
20
2
相同
丁
5
10
25
2
相同
实验序号
温度t（℃）
液柱高度h（cm）
1
0
5
2
10
7
3
30
11
4
60
17
5
100
25
实验序号
温度t（℃）
液柱高度h（cm）
6
0
6
7
5
7.5
8
15
10.5
9
30
15
10
60
24